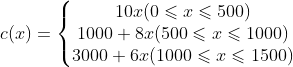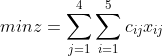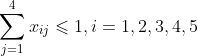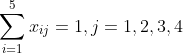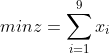数学规划（Python cvxpy、scipy.optimize）

一、线性规划模型 

1.模型结构

①决策变量，x =（x1,x2,x3…,xn）。

②目标函数，f(x) 

③可行域，，常用一组不等式(约束条件)表示：

当目标函数和约束条件对于决策变量而言都是线性的时，称为线性规划

2.模型特征

①比例性，决策变量对目标函数和约束条件的“贡献”，与决策变量的取值成正比

②可加性，决策变量对目标函数和约束条件的“贡献”，与决策变量的取值无关

③连续性，决策变量的取值是连续的

二、线性规划模型求解

（以数学模型第86页模型为例）

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5) 

2.代码求解

import cvxpy as cp
import numpy as np

coef = np.array([72, 64])#输入目标函数系数
left = np.array([[1, 1], [12, 8], [3, 0]])#输入约束条件系数
right = np.array([50, 480, 100])#输入约束条件上限值
x = cp.Variable(2)#构造决策变量
obj = cp.Maximize(coef @ x)#构造目标函数
cons = [x >= 0, left @ x <= right]#构造约束条件
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver='CPLEX')#模型求解
print("最优值:", prob.value)
print("最优解:", x.value)
print("剩余牛奶：", right[0] - sum(left[0] * x.value))
print("剩余劳动时间：", right[1] - sum(left[1] * x.value))
print("A1剩余加工能力：", right[2] - sum(left[2] * x.value))

3.输出结果

最优值: 3360.0
最优解: [20. 30.]
剩余牛奶： 0.0
剩余劳动时间： 0.0
A1剩余加工能力： 40.0

三、结果分析

1.有效约束

约束条件的右端不妨称为“资源”，目标函数不妨称为“效益”。

若“资源”在最优解下的剩余为0，则称该约束为有效约束。

2.影子价格

当成为有效约束的“资源”增加，“效益”必然会增长。

“资源”增加带来的“效益”的增量可以看作“资源”的潜在价值，称为影子价格

四、复杂线性规划模型举例

（以数学模型第96页模型为例）

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5) 

(6) 

(7) 

(8) 

(9) 

2.代码求解

import cvxpy as cp
import numpy as np
#输入目标函数系数
coef = np.array([160, 130, 220, 170,
                 140, 130, 190, 150,
                 190, 200, 230])
#输入约束条件系数
left = np.array([[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0],
                 [0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0],
                 [0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1],
                 [0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0]])
right_min = np.array([30, 70, 10, 10])#输入约束条件下限值
right_max = np.array([80, 140, 30, 50])#输入约束条件上限值
x = cp.Variable(11)#构造决策变量
obj = cp.Minimize(coef @ x)#构造目标函数
#构造约束条件
cons = [x >= 0,
        left @ x <= right_max,
        left @ x >= right_min,
        cp.sum(x[0:4]) == 50,
        cp.sum(x[4:8]) == 60,
        cp.sum(x[8:11]) == 50]
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver="CPLEX")#模型求解
print("管理费用最小值为：", prob.value)
print("最优分配方案为：", x.value)

3.输出结果

管理费用最小值为： 24400.0
最优分配方案为： [ 0. 50.  0.  0.  0. 50.  0. 10. 40.  0. 10.]

五、整数规划模型

在线性规划模型中，增加约束条件使得决策变量均为整数，这样得到的新模型就称为整数规划

例一

（以数学模型第101页为例）

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5)  均为整数

2.代码求解

import cvxpy as cp
import numpy as np

coef = np.array([2, 3, 4])#输入目标函数系数
left = np.array([[1.5, 3, 5], [280, 250, 400]])#输入约束条件系数
right = np.array([600, 60000])#输入输入约束条件上限值
x = cp.Variable(3, integer=True)#创建决策变量，并且为整数
obj = cp.Maximize(coef @ x)#构造目标函数
cons = [x >= 0, left @ x <= right]#构造约束条件
prob = cp.Problem(obj, cons)#构建模型
prob.solve(solver="CPLEX")#模型求解
print("最优值：", prob.value)
print("最优解：", x.value)
print("钢材剩余量：", right[0] - sum(left[0] * x.value))
print("劳动时间剩余量：", right[1] - sum(left[1] * x.value))

3.输出结果

最优值： 632.0
最优解： [ 64. 168.   0.]
钢材剩余量： 0.0
劳动时间剩余量： 80.0

例二

（以数学模型第103页解法二为例）

在例一的基础上，增加新的约束条件——“如果生成某一类型汽车，则至少要生产80辆”，选择引入0-1变量，化为整数规划

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5)  均为整数

(6) 

(7) 

(8) 

对于约束条件(6)-(8)，0-1变量y的存在就是为了控制决策变量x的范围，约束条件的上限就是为了保证y等于0时，决策变量x也一定为0。因此M的取值无需对决策变量x产生影响，取值时只需保证足够大即可。

2.代码求解

import cvxpy as cp
import numpy as np

coef = np.array([2, 3, 4])
left = np.array([[1.5, 3, 5], [280, 250, 400]])
right = np.array([600, 60000])
x = cp.Variable(3, integer=True)
y = cp.Variable(3, integer=True)
obj = cp.Maximize(coef @ x)
cons = [x >= 0, left @ x <= right,
        y >= 0, y <= 1,
        x[0] >= 80 * y[0], x[0] <= 1000 * y[0],
        x[1] >= 80 * y[1], x[1] <= 1000 * y[1],
        x[2] >= 80 * y[2], x[2] <= 1000 * y[2], ]
prob = cp.Problem(obj, cons)
prob.solve(solver="CPLEX")
print("最优值：", prob.value)
print("最优解：", x.value)
print("钢材剩余量：", right[0] - sum(left[0] * x.value))
print("劳动时间剩余量：", right[1] - sum(left[1] * x.value))

3.输出结果

最优值： 610.0
最优解： [ 80. 150.   0.]
钢材剩余量： 30.0
劳动时间剩余量： 100.0

六、复杂整数规划模型求解

（以数学模型第107页解法三为例）

该模型的难点在于对分段函数进行变换，使得其可以使用线性规划、整数规划模型加以处理。

1.基本模型

(1)  

(2) 

(3) 

(4) 

(5) 

(6) 

(7) 

(8) 

(9) 

(10) 

(11) 

(12) 

(13) 

约束条件(9)-(11)是对分段函数(1)转换得到的；每个z都是对分段函数每个分点的表示，两个相邻的z可以确定对应段x的取值；每个0-1变量y指的是是否在该分段；条件(12),(13)可用变量z表示x和c(x)。

2.代码求解

import cvxpy as cp
import numpy as np

coef_x = np.array([4.8, 5.6, 4.8, 5.6])#输入目标函数x对应系数
coef_cx = np.array([0, 5000, 9000, 12000])#输入用z表示cx的系数
coef_buy_x = np.array([0, 500, 1000, 1500])#输入用z表示x的系数
left = np.array([[0, 0, 1, 1], [-1, 0, 1, 0], [0, -2, 0, 3]])#输入约束条件系数
right = np.array([1000, 0, 0])#输入约束条件上限值
x = cp.Variable(4)#创建决策变量x
y = cp.Variable(3, integer=True)#创建0-1变量y
z = cp.Variable(4)#创建变量z
obj = cp.Maximize(coef_x @ x - coef_cx @ z)#构造目标函数
#构造约束条件
cons = [cp.sum(x[0:2]) <= 500 + cp.sum(coef_buy_x @ z),
        left @ x <= right,
        sum(coef_buy_x @ z) <= 1500,
        x >= 0,
        z[0] <= y[0], z[1] <= y[0] + y[1], z[2] <= y[1] + y[2], z[3] <= y[2],
        cp.sum(z[:]) == 1, z >= 0,
        cp.sum(y[:]) == 1,
        y >= 0, y <= 1]
prob = cp.Problem(obj, cons)#构造模型
prob.solve(solver="CPLEX")#求解模型
print("最优值：", prob.value)
print("最优解：", x.value)
print("购买原油A：", sum(coef_buy_x * z.value), "t")

3.输出结果

最优值： 5000.0
最优解： [   0. 1500.    0. 1000.]
购买原油A： 1000.0 t

七、0-1规划模型

在线性规划模型中，增加决策变量只能为0或1的约束条件，这样得到的模型就称为0-1规划模型

 （以数学模型第110页为例）

1.基本模型

(1) 

(2) 

(3) 

(4) 

2.代码求解

import cvxpy as cp
import numpy as np
#输入目标函数系数
coef = np.array([66.8, 75.6, 87, 58.6,
                 57.2, 66, 66.4, 53,
                 78, 67.8, 84.6, 59.4,
                 70, 74.2, 69.6, 57.2,
                 67.4, 71, 83.8, 62.4])
x = cp.Variable(20, integer=True)#构造决策变量
#构造目标函数
obj = cp.Minimize(coef @ x)
#输入约束条件
cons = [x >= 0, x <= 1,
        cp.sum(x[0:4]) <= 1,
        cp.sum(x[4:8]) <= 1,
        cp.sum(x[8:12]) <= 1,
        cp.sum(x[12:16]) <= 1,
        cp.sum(x[16:20]) <= 1,
        cp.sum(x[0:20:4]) == 1,
        cp.sum(x[1:20:4]) == 1,
        cp.sum(x[2:20:4]) == 1,
        cp.sum(x[3:20:4]) == 1]
prob = cp.Problem(obj, cons)#构造模型
prob.solve(solver="CPLEX")#模型求解
print("最优值：", prob.value)
print("最优解：", x.value)

3.输出结果

最优值： 253.2
最优解： [ 0. -0. -0.  1.  1. -0. -0.  0. -0.  1. -0. -0. -0. -0.  1.  0. -0. -0. -0. -0.]

八、多目标规划模型

只有一个优化目标的规划问题称为单目标规划，而将多于一个目标的规划问题称为多目标规划。

多目标规划的目标函数可以表示为一个向量：  ,"V-min"是向量最小化的意思，

对于任意最大化目标a，只需在a前加负号即可统一为最小化问题

（以数学模型第113页同学丙为例）

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5) 

(6) 

(7) 

(8) 

(9) 

(10) 

(11) 

(12) 

(13) 

2.代码求解

import cvxpy as cp
import numpy as np
#输入目标函数的系数
coef_obj = np.array([-0.8, -0.5, -0.5, -0.2, -0.5, -0.2, 0.1, 0.1, -0.2])
coef_credits = np.array([5, 4, 4, 3, 4, 3, 2, 2, 3])#输入课程学分系数
x = cp.Variable(9, integer=True)#构造决策变量
obj = cp.Minimize(coef_obj @ x)#构造目标函数
#输入约束条件
cons = [cp.sum(x[0:5]) >= 2,
        x[2] + [4] + x[5] + x[7] + x[8] >= 3,
        x[3] + x[5] + x[6] + x[8] >= 2,
        2 * x[2] - x[0] - x[1] <= 0,
        x[3] - x[6] <= 0,
        2 * x[4] - x[0] - x[1] <= 0,
        x[5] - x[6] <= 0,
        x[7] - x[4] <= 0,
        2 * x[8] - x[0] - x[2] <= 0,
        x >= 0, x <= 1]
prob = cp.Problem(obj, cons)#模型构建
prob.solve(solver="CPLEX")#模型求解
print("选课结果：", x.value)
print("学分总和：", sum(coef_credits * x.value))

3.输出结果

选课结果： [ 1.  1.  1.  1.  1.  1.  1. -0.  1.]
学分总和： 28.0

九、非线性规划模型

若数学规划模型的目标函数或约束条件对于决策变量而言是非线性的，则称为非线性规划。 

由于CVXPY库处理非线性函数需要区分凸函数、非凸函数等，比较复杂；而SCIPY库可以处理任意非线性规划模型，因此决定用SCIPY求解非线性规划模型

例一

1.基本模型

(1) 

(2) 

(3) 

2.代码求解

from scipy.optimize import minimize
import numpy as np

#输入目标函数
def obj(x):
    return x[0] ** 3 - x[1] ** 3 + x[0] * x[1] + 2 * x[0] ** 2

#输入第一个约束条件
def cons1(x):
    return -x[0] ** 2 - x[1] ** 2 + 6

#输入第二个目标函数
def cons2(x):
    return x[0] * x[1] - 2

#初始化
x0 = np.zeros(2)
x0[0] = 1
x0[1] = 2

bound = (0, 3)#输入决策变量范围
bounds = (bound, bound)#构造决策变量界限
#构造约束条件
cons1 = {"type": "ineq", "fun": cons1}
cons2 = {"type": "eq", "fun": cons2}
cons = ([cons1, cons2])
#构造模型
prob = minimize(obj, x0, method="SLSQP", bounds=bounds, constraints=cons)
#模型求解
x = prob.x
print("最优值：", obj(x))
print("最优解：", x[0], x[1])

 需要注意的是

① 对于“ineq”（即大于等于，小于等于等），约束条件默认的格式是 ，因此需要对模型中约束条件进行标准化再输入

② 初始化这一步骤不可省略

3.输出结果

最优值： -7.785844454002188
最优解： 0.8740320488968545 2.2882456112715115

例二

1.基本模型

(1) 

(2) 

(3) 

(4) 

(5) 

2.代码求解

from scipy.optimize import minimize
import numpy as np

#输入目标函数
def obj(x):
    return 0.5 * x[0] ** 2 + x[1] ** 2 - x[0] * x[1] - 2 * x[0] - 6 * x[1]

#输入第一个约束条件
def cons1(x):
    return 2 - x[0] - x[1]

#输入第二个约束条件
def cons2(x):
    return 2 + x[0] - 2 * x[1]

#输入第三个约束条件
def cons3(x):
    return 3 - 2 * x[0] - x[1]

#初始化
x0 = np.zeros(2)
x0[0] = 0
x0[1] = 1
#输入决策变量范围
bound = (0, None)
#构造决策变量界限
bounds = (bound, bound)
#构造约束条件
cons1 = {"type": "ineq", "fun": cons1}
cons2 = {"type": "ineq", "fun": cons2}
cons3 = {"type": "ineq", "fun": cons3}
cons = ([cons1, cons2, cons3])
#构造模型
prob = minimize(obj, x0, method="SLSQP", bounds=bounds, constraints=cons)
#模型求解
x = prob.x
print("最优值：", obj(x))
print("最优解：", x[0], x[1])

3.输出结果

最优值： -8.222222222222175
最优解： 0.6666666666666612 1.333333333333325