【lzy学习笔记-dive into deep learning】数学预备 2.1-2.4

2.1 数据操作(张量)

完成数据操作需要: ①存储数据和②操作数据
张量tensor：n维数组（深度学习框架中的张量类，PyTorch和TensorFlow为Tensor）。
张量表示由一个数值组成的数组，这个数组可能有多个维度。具有一个轴的张量对应数学上的向量vector；具有两个轴的张量对应数学上的矩阵matrix；具有两个轴以上的张量没有特殊的数学名称。
张量中的每一个值成为张量的元素element。除非额外指定，新的张量将存储在内存中，并采用基于CPU的计算。

import torch # 导入PyTorch

x = torch.arange(12) # arange创建行向量
# 默认创建整数，也可创建类型为浮点数
# 包含从0开始的前12个整数
print(x)

print(x.shape) # 张量的shape属性访问张量（沿每个轴的长度）的形状

print(x.numel()) # 张量中元素的总数

X = x.reshape(3,4) # 不会改变元素数量和元素值，仅改变张量的形状
# X = x.reshape(3,-1)
# X = x.reshape(-1,4) # -1 自动计算维度
print(X)

print(torch.zeros((2,3,4))) # 全0

print(torch.ones((2,3,4))) # 全1

# 从某个特定的概率分布中随机采样得到张量中的元素数值
# 从均值为0、标准差为1的标准高斯分布（正态分布）中随机采样
print(torch.randn(3,4))

# 包含数值的Python列表（或嵌套列表）
print(torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]))

运算符
对于任意具有相同形状的张量，常⻅的标准算术运算符都可以被升级为按元素运算，即按元素运算将⼆元运算符应⽤于两个数组中的每对位置对应的元素。

import torch

# 1.按元素运算
x = torch.tensor([1.0,2,4,8])
y = torch.tensor([2,2,2,2])
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print(x**y)
print(torch.exp(x)) # 求幂

# 2.张量连结
X = torch.arange(12,dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
print(torch.cat((X,Y),dim=0)) # 沿行，轴-0，改形状的第⼀个元素 --> (6,4)
print(torch.cat((X,Y),dim=1)) # 沿列，轴-1，改形状的第二个元素 --> (3,8)

# 3.通过逻辑运算符构建⼆元张量
print(X == Y)

# 4.对张量中的所有元素进⾏求和，会产⽣⼀个单元素张量
print(X.sum())

广播机制broadcasting mechanism
在某些情况下，即使形状不同，仍然可以通过调⽤⼴播机制来执⾏按元素操作。
工作方式：⾸先，通过适当复制元素来扩展⼀个或两个数组，以便在转换之后，两个张量具有相同的形状。其次，对⽣成的数组执⾏按元素操作。

# 广播机制
import torch
# 在大多数情况下，沿着数组中长度为1的轴进行广播
a = torch.arange(3).reshape((1,3))
b = torch.tensor([[5],[6]])
print(a)
print(b)
print(a+b)

索引与切片
与任何Python数组⼀样：
第⼀个元素的索引是0，最后⼀个元素索引是-1；
可以指定范围以包含第⼀个元素和最后⼀个之前的元素

import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
# 读取
print(X[-1]) # 最后一个元素
print(X[1:3]) # 第2 3个元素
# 写入
X[1,2] = 9
# 想为多个元素赋值相同的值，只需要索引所有元素，然后为它们赋值
X[0:2, :] = 12 # 第1 2行，所有列

节省内存
运⾏⼀些操作可能会导致为新结果分配内存。
该行为的弊端：在机器学习中，我们可能有数百兆的参数，并且在⼀秒内多次更新所有参数。通常情况下，我们希望原地执⾏这些更新。其次，如果我们不原地更新，其他引⽤仍然会指向旧的内存位置，这样我们的某些代码可能会⽆意中引⽤旧的参数。
执行原地操作⾮常简单。我们可以使⽤切片表示法将操作的结果分配给先前分配的数组，例如Y[:] = expression

import torch

# python id() 提供了内存中引⽤对象的确切地址
X = torch.tensor([1.0,2,4,8])
Y = torch.tensor([2,2,2,2])
Z = torch.zeros_like(Y) # 分配⼀个全0的块,其形状与另⼀个Y相同
print(id(Z))
Z[:] = X + Y
print(id(Z)) # same

# 如果在后续计算中没有重复使⽤X，减少操作的内存开销
before = id(X)
# X[:] = X + Y
X += Y
print(id(X) == before) # True

转化为其它python对象

import torch

# 深度学习框架定义的张量《-》NumPy张量ndarray
X = torch.tensor([1.0,2,4,8])
A = X.numpy()
B = torch.tensor(A)
print(type(A), type(B))

# 将⼤小为1的张量转换为Python标量
# 可以调⽤item函数或Python的内置函数
a = torch.tensor([3.5])
print(a, a.item(), float(a), int(a))

深度学习存储和操作数据的主要接口是张量（n维数组）。它提供了各种功能，包括基本数学运算、广播、索引、切片、内存节省和转换其他Python对象。

2.2 数据预处理

经常从预处理原始数据开始，而不是从那些准备好的张量格式数据开始。
pandas软件包可以与张量兼容。经常被使用
读取数据集
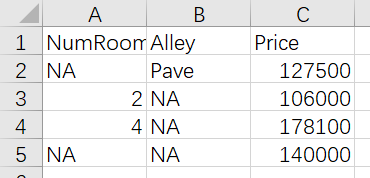
⾸先创建⼀个⼈⼯数据集，并存储在CSV逗号分隔值⽂件。
以其他格式存储的数据也可以通过类似的⽅式进⾏处理。
下⾯我们将数据集按⾏写⼊CSV⽂件中。

import os
os.makedirs(os.path.join('F:','codeTry'),exist_ok=True)
data_file = os.path.join('F:','codeTry','house_tiny.csv')
with open(data_file,'w') as f:
    f.write('NumRooms,Alley,Price\n')
    f.write('NA,Pave,127500\n')
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

在对应的文件路径下有新建csv文件

要从创建的CSV⽂件中加载原始数据集，我们导⼊pandas包并调⽤read_csv函数。
安装：命令行执行pip install pandas

import os
import pandas as pd
data_file = os.path.join('F:','codeTry','house_tiny.csv')
data = pd.read_csv(data_file)
print(data)

处理缺失值
为了处理缺失的数据，典型的⽅法包括插值法和删除法，其中插值法⽤⼀个替
代值弥补缺失值，而删除法则直接忽略缺失值。

# 插值法
import os
import pandas as pd
data_file = os.path.join('F:','codeTry','house_tiny.csv')
data = pd.read_csv(data_file)
#对于数值型
inputs,outputs = data.iloc[:,0:3],data.iloc[:,3] #位置索引iloc
inputs = inputs.fillna(inputs.mean()) #⽤同⼀列的均值替换“NaN”项(数值列)
#对于类别值或者离散值
inputs = pd.get_dummies(inputs,dummy_na=True)
# 由于“巷⼦类型”（“Alley”）列只接受两种类型的类别值“Pave”和“NaN”
# pandas可以⾃动将此列转换为两列“Alley_Pave”和“Alley_nan”
# 巷⼦类型为“Pave”的⾏会将“Alley_Pave”的值设置为1，“Alley_nan”的值设置为0。
# 缺少巷⼦类型的⾏会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
print(inputs)

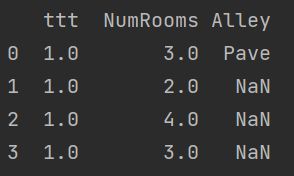
转化成张量格式
现在所有条⽬都是数值类型，它们可以转换为张量格式。

# 插值法
import os
import pandas as pd
import torch
data_file = os.path.join('F:','codeTry','house_tiny.csv')
data = pd.read_csv(data_file)
#对于数值型
inputs,outputs = data.iloc[:,0:3],data.iloc[:,3] #位置索引iloc
inputs = inputs.fillna(inputs.mean()) #⽤同⼀列的均值替换“NaN”项(数值列)
#对于类别值或者离散值
inputs = pd.get_dummies(inputs,dummy_na=True)
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(X)
print(y)

小结：
• pandas软件包是Python中常⽤的数据分析⼯具中，pandas可以与张量兼容。
• ⽤pandas处理缺失的数据时，我们可根据情况选择⽤插值法和删除法。

2.3 线性代数

标量
称仅包含⼀个数值的叫标量scalar。标量由只有⼀个元素的张量表⽰。
变量variable表⽰未知的标量值

# 实例化两个标量
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
print(x+y,x-y,x*y,x/y,x**y)

向量
可以将向量视为标量值组成的列表。我们将这些标量值称为向量的元素element或分量component。
通过⼀维张量处理向量，通过张量的索引来访问任⼀元素。
⼀般来说，张量可以具有任意⻓度，取决于机器的内存限制。
实际中可以用一个向量代表一个样本。
大量文献认为列向量是向量的默认方向
向量只是⼀个数字数组，⼀个向量x由n个实值标量组成，可以表⽰为x ∈ Rn
向量的⻓度通常称为向量的维度dimension。
矩阵
矩阵在代码中表示为具有两个轴的张量
形状为正方形时是方阵square matrix
交换矩阵的行与列，称为矩阵的转置transpose B=AT bij=aji
尽管单个向量的默认方向是列向量，但在表示表格数据集的矩阵中，将每个数据样本作为矩阵中的行向量更为常见。

import torch

# 实例化矩阵：指定两个分量
A = torch.arange(20).reshape(5,4)

# 矩阵转置
print(A.T)

# 对称矩阵 A=AT
B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
print(B == B.T)

张量
张量（本小节中的“张量”指代数对象）为我们提供了描述具有任意数量轴的n维数组的通⽤⽅法。
例如，向量是⼀阶张量，矩阵是⼆阶张量。张量的索引机制与矩阵类似。
开始处理图像时，张量将变得更加重要，图像以n维数组形式出现，其中3个轴对应于⾼度、宽度，以及⼀个通道channel轴，⽤于表⽰颜⾊通道（红⾊、绿⾊和蓝⾊）

X = torch.arange(24).reshape(2,3,4)

张量算法的基本性质

import torch

# 形状相同按元素运算
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
B = A.clone() # 分配新内存
print(A+B)

# 矩阵按元素乘法 Hadamard积
print(A*B)

# 标量 * + 张量
# 将张量乘以或加上⼀个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘
a = 2
X = torch.arange(24).reshape(2,3,4)
print(a+X)
print((a*X).shape)

降维

import torch

# 降维求和 任意形状张量的元素和
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
print(A)
print(A.sum())
# 默认情况下，调⽤求和函数会沿所有的轴降低张量的维度，使它变为⼀个标量

# 可以指定张量沿哪⼀个轴来通过求和降低维度
# 输⼊轴的维数在输出形状中消失
A_sum_axis0 = A.sum(axis=0) #降维行消失,只有列,按列求和
print(A_sum_axis0)
print(A_sum_axis0.shape)

A_sum_axis1 = A.sum(axis=1) #降维列消失,只有行
print(A_sum_axis1)
print(A_sum_axis1.shape)

print(A.sum(axis=[0,1])) #=A.sum()

# 求均值
print(A.mean())
print(A.sum()/A.numel())
# 指定轴降维
print(A.mean(axis=0))
print(A.sum(axis=0)/A.numel())

非降维求和
有时在调⽤函数来计算总和或均值时保持轴数不变会很有⽤。

import torch

A = torch.arange(20,dtype=torch.float32).reshape(5,4)
print(A)

sum_A = A.sum(axis=1, keepdims=True) # 在对每行求和后仍保持两个轴
print(sum_A)

print(A + sum_A) # 广播

print(A.cumsum(axis=0)) # 沿某个轴计算A元素的累积总和
# 此函数不会沿任何轴降低输⼊张量的维度。

点积Dot Product

import torch

# 计算点积法1
x = torch.arange(4,dtype= torch.float32)
y = torch.ones(4, dtype = torch.float32)
print(torch.dot(x, y))

# 法2
print(torch.sum(x * y))

矩阵-向量积matrix-vector product
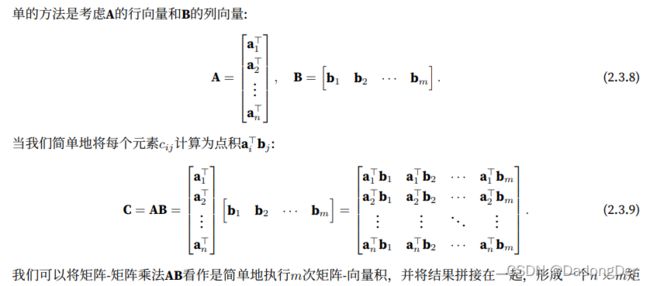
矩阵乘法可以看做是一个从Rn到Rm向量的转化

import torch

# A的列维数（沿轴1的⻓度）必须与x的维数（其⻓度）相同
x = torch.arange(4,dtype= torch.float32)
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
print(torch.mv(A,x))
print(torch.mv(A,x).shape)

矩阵-矩阵乘法/矩阵乘法

import torch
A = torch.arange(20,dtype=torch.float32).reshape(5,4)
B = torch.ones(4,3)
print(torch.mm(A,B))
print(torch.mm(A,B).shape)

区分矩阵乘法和Hadamard积
范数
⼤小size概念不涉及维度，而是分量的⼤小
向量范数的性质：


常见的向量范数：L1 L2 LP



矩阵范数：Frobenius

import torch
u = torch.tensor([3.0, -4.0])
torch.norm(u) # L2
torch.abs(u).sum() # L1
torch.norm(torch.ones((4, 9))) #Frobenius

⼩结
• 标量、向量、矩阵和张量是线性代数中的基本数学对象。
• 向量泛化⾃标量，矩阵泛化⾃向量。
• 标量、向量、矩阵和张量分别具有零、⼀、⼆和任意数量的轴。
• ⼀个张量可以通过sum和mean沿指定的轴降低维度。
• 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。
• 在深度学习中，我们经常使⽤范数，如L1范数、L2范数和Frobenius范数。
• 我们可以对标量、向量、矩阵和张量执⾏各种操作。

2.4 微积分

微分学最重要的应用是优化问题
在深度学习中，训练模型不断更新它们，使模型在看到越来愈多的数据时变得越来越好。通常变得更好这意味着最小化一个损失函数loss fucntion，即一个衡量我们的模型有多糟糕这个问题的分数。最终真正关心的是生成一个模型，能在从未见过的数据上表现良好。但是训练模型只能将模型与实际看到的数据相拟合。因此***将拟合模型的任务分解为两个关键问题：***①优化optimization：用模型拟合观测数据的过程；②泛化generalization：数学原理和实践者的智慧，能够指导我们生成有效性超出用于训练的数据集本身的模型。
导数与微分

import numpy as np
import matplotlib.pyplot as plt # Python中流⾏的绘图库

# 微分思想
def f(x): # f(x) = 3 x ** 2 − 4x
    return 3 * x ** 2- 4 * x

def numerical_lim(f,x,h): # 对h取极限
    return (f(x+h) - f(x)) / h

h = 0.1 # h越小越趋近于导数
for i in range(5):
    print(f'h={h:.5f},numerical limit={numerical_lim(f,1,h):.5f}')
    h *= 0.1

# 图像可视化
x = np.arange(0,3,0.1) # 横轴范围
plt.plot(x,f(x),label="f(x)") # 自变量 因变量
plt.plot(x,2*x-3,label="tangent line(x=1)",linestyle="--")
plt.xlabel('x') # 轴标
plt.ylabel("f(x)")
plt.legend() # 左上角图标
plt.show()

偏导数

梯度
梯度定义：包含n个偏导数的向量

微分多元函数规则：向量、矩阵

链式法则
实际很难应用以上规则微分函数
链式法则能微分复合函数composite

小结
• 微分和积分是微积分的两个分⽀，前者可以应⽤于深度学习中的优化问题。
• 导数可以被解释为函数相对于其变量的瞬时变化率，它也是函数曲线的切线的斜率。
• 梯度是⼀个向量，其分量是多变量函数相对于其所有变量的偏导数。
• 链式法则使我们能够微分复合函数。