matlab 支撑集,基于OMP算法的快速压缩感知图像重构

引用本文

马博珩, 彭艺. 基于OMP算法的快速压缩感知图像重构[J].云南大学学报(自然科学版), 2017,39(2): 207-211.

MA Bo-heng, PENG Yi. Fast compressed sensing image reconstruction based on OMP algorithm[J]. Journal of Yunnan University(Natural Sciences), 2017,39(2): 207-211.

DOI:10.7540/j.ynu.20160247

Permissions

Copyright©2017, 《云南大学学报(自然科学版)》编辑部

《云南大学学报(自然科学版)》编辑部 所有

基于OMP算法的快速压缩感知图像重构

马博珩, 彭艺

昆明理工大学 信息工程与自动化学院,云南 昆明 650500

通讯作者: 彭 艺(1975-),女,云南人,博士,副教授,主要研究方向为无线通信.

作者简介: 马博珩(1992-),男,北京人,研究生,主要研究方向为压缩感知.E-mail:[email protected].

收稿日期: 2016-05-04

基金资助: 云南省科技厅面上项目(KKS0201403016).

摘要

针对正交匹配追踪(OMP)算法在压缩感知理论下的重构效果和所需时间相互矛盾的问题,基于子空间追踪(SP)算法的回溯思想,使用共轭梯度下降算法代替最小二乘法对正交匹配追踪(OMP)算法进行改进.并且对所改进算法的重构精度、重构稳定性进行了仿真实验,结果表明所提算法能保证重构质量良好并且有更好的重构速度和稳定性.

关键词:

压缩感知; OMP算法; 信号重构; 图像重构

中图分类号:TN911.72

文献标志码:A

文章编号:0258-7971(2017)02-0207-05

Fast compressed sensing image reconstruction based on OMP algorithm

MA Bo-heng, PENG Yi

Institute of Information and Automation,Kunming University of Science and Technology,Kunming 650500,China

Abstract

This paper proposed an improved OMP(Orthogonal Matching Pursuit)algorithm that replaced Ordinary Least Square algorithm with Conjugate Gradient Descent algorithm based on the backfitting idea of Subspace Pursuit algorithm,in order to solve the problem of contradiction between reconstruction effort and time required of OMP algorithm under compressive sensing theory.This paper also made simulation experiment on the accuracy and stability of reconstruction of the improved algorithm.The result showed that the improved algorithm made the quality of reconstruction satisfying with better speed and stability of reconstruction.

Keyword:

compressed sensing(CS); Orthogonal Matching Pursuit algorithm (OMP); signal reconstruction; image reconstruction

压缩感知技术(compressed sensing, CS)是一种用于信号采样的新理论[.传统的信息采样是基于Nyqiust采样定理, 认为信号的采样率只有不低于最高频率的2倍, 信号才能被精确地重构.但是压缩感知理论指出, 若一个信号是稀疏信号或是可以在某个变换域上表现为稀疏信号, 那么可以通过一个与变换基并不相关的矩阵将此信号投影到低维空间上.这一在低维空间上的投影, 包含了原信号的全部信息可以精确地重构出原信号.在压缩感知理论下, 信号采样并不是直接测量信号本身, 其关键在于梳理信息在信号中的结构与内容[.

压缩感知理论由Donoho和Candes等在2004年首次提出来, 目前压缩感知理论的主要研究方向[分为信号稀疏性、测量矩阵和重构算法这3大部分.压缩感知中的采样过程相对简单, 但重构非常复杂, 所以对于重构算法的研究是压缩感知中相当重要的一方面[.目前来说, 重构算法中贪婪迭代算法是应用非常广泛的一类, 该类算法通过迭代方式来选出信号的最佳支撑, 之后基于贪婪准则选择局部最优解, 逐步逼近原始信号.最典型的贪婪算法是匹配追踪算法(Matching Pursuit), 以及在其基础上改进的正交匹配追踪算法(Orthogonal Matching Pursuit)[.本文将针对OMP算法重构时间较长的问题, 结合子空间追踪(SP)算法的思想, 引入共轭梯度下降算法代替最小二乘法, 对正交匹配追踪(OMP)算法进行改进以及重构仿真实验.

1 压缩感知理论

在CS理论下, 需要传输的信号并非是原始信号本身的采样值, 而是原始信号在某个稀疏域上的投影.压缩感知本质是一种非线性压缩信号以及重建的方法.设有一维信号x∈ R, 信号长N位, x=[x1, x2, x3, …, xn].RN内任何信号都可用M× N维的正交基向量Ψ =[Ψ1, Ψ2, …, Ψ a]的线性组合表示, 即 i, 其中系数α =[α1, α2, α3, …, α n].如果系数向量α中最多有K个非零的元素存在, 那么可以认为信号x是K-稀疏信号.而依据压缩感知理论所述, 对于所有 ≤ K的信号, 都存在一个常数δ∈ (0, 1), 使得

(1-δ) x22≤ Φx22≤ (1+δ) x22

成立, 其中δ称为等距常数, 为上式成立的最小值.当其成立时, 则认为观测矩阵Φ满足有限等距性质(RIP).此时存在观测方程y=Φ x, y∈ RM为x在观察矩阵Φ M× N上投影为M×1维的观察向量.这时可以利用y中至少M≥ K×log(N/K)个观察值将原信号还原出来.由于其中M≪N, 所以采样的信号并不完全, 称为欠采样, 正对K-稀疏信号, 可以通过重构模型min x0, s.t.y=Φ x进行信号还原, 因为y=Φ x是存在多个解的, 这是一个NP-hard问题[.因此通过间接方式进行求解或是将其转换为l1范数min x1, s.t.y=Φ x求解问题[.

2 正交匹配追踪算法OMP算法

OMP算法是在MP算法的基础上进行改进的, 在沿用了MP算法原子选择标准而来, 来甄选相关性最大的原子.同时通过对已选原子集的正交投影化改进MP算法迭代选择中出现的次优问题

OMP算法步骤

输入 观测矩阵Φ, 观测向量y, 迭代次数为K

输出 还原信号 x˙

Step 1 初始化 设迭代次数t=1, 残差rt=y, 支撑集索引Λ为空集;

Step 2 计算残差rt与观察矩阵的列向量ϕ j, 内积中的最大值所对应的索引, 即

λ t=arg maxj=1, 2,3K,…,n;

Step 3 更新索引集Λ, 使Λ t=Λ t-1∪ {λ1}, 更新原子集Φ t=[Φ t, ϕλt], 将内积最大值所对应观察矩阵列向量ϕ λ t记入原子集;

Step 4 运用最小二乘法计算 x˙使残差最小

x˙=arg min y-Φtx˙2;

Step 5 更新残差rt=y-Φ t x˙, 令迭代次数增加1;

判断 停止条件(迭代次数< k)如果不成立执行Step 2, 若是成立则停止迭代输出 x˙.

OMP算法的基本思想是依据内积选择观察矩阵的列, 使得选择的列与当前残差到达最大相关, 之后在残差中减去相关的部分信号, 再重复上述步骤直到迭代次数到达稀疏度K.

OMP算法利用已选择的原子集合的正交化来保证迭代的局部最优解.但是无法保证局部最优解的和是全局最优解.而SP算法在重构过程中引入了回溯思想, 既是使得选入信号支撑集的元素并非永久性保存, 而是随着迭代的进行, 对于支撑集中已经存在的原子进行再次计算, 剔除其中非最优的原子, 并且依据现在迭代环节加入最优原子, 其目的在于以使局部最优解尽量接近于全局最优[.

通过Matlab仿真分析, 结果如图1(实验采样率为60%), 可见与引入“ 回溯” 的思想的SP算法, OMP 算法得到欠定方程最优解的时间明显更短, 但是重构质量相对较差.

图1

Fig1.图1 SP算法与OMP算法重构效果对比Fig1. Comparison of reconstruction effort of SP and OMP

3 针对OMP算法的改进

OMP算法在计算中需要使用最小二乘法进行测量信号的计算, 但最小二乘法本质上是求解样本观测值与估计值的残差平方和最小的极值问题的一种方法, 在非经典线性问题求解上精度并不高, 使得信号重构过程中残差更新的误差逐渐积累, 降低重构质量

3.1 共轭梯度下降算法

共轭梯度法(conjugate gradient method, CG), 最初是为求解正定系数矩阵线性方程组而提出的[.进而被应用于无约束最优问题.共轭梯度法作为典型的共轭方向法, 其任意搜索方向是互相共轭的

使用共轭梯度法求解Ax=B, 在A是对称正定矩阵时等价于求解二次最优化问题即

min f(x)= 12xTAx+bTx, 其中, x0∈ Rn, A是对称正定矩阵[.

相关定义:

(1) 若矩阵A对称, 且对任意的x0∈ Rn, x≠ 0, 有xTAx≥ 0, 则称A是对称正定矩阵.

(2) 设A∈ RM× n为正定矩阵, 若Rn中非零向量D=[d1, d2, d3, …, dn]满足 dTiAdj=0, ∀ i, j=0, 1, 2, …, m-1, i≠ j, 则称向量组D是A的共轭向量组, 且这m个向量线性无关.此时从任一点x0∈ Rn出发依次延向量组D进行搜索, 则最多仅需要经过n次迭代计算就可得到最优解.

(3) 在共轭梯度法中取初始点x(0), 第1次搜索方向则为d(0)=-∇f(x(0)).之后以每次新的共轭方向d(k+1)可以由k次迭代的负梯度g(x)=-∇f(x(k+1)与以解共轭向量的线性组合确定, 即d(k+1)=-gk+1+β kd(k).

新的搜索方向与上次搜索方向相垂直, 可见共轭是正交的扩展概念, 由于d(k+1)与d(k)关于A共轭, 可解出β k= d(k)TAgk+1d(k)TAdk.求解新的迭代点xk+1=xk+α kdk, 从向方向xk处向d(k)方向取极小值.步长ak= (dk,rk)(Adk,dk), 其中rk=rk-1-α kA dk[15-16, 18].

3.2 针对OMP算法的改进算法

共轭梯度法收敛快, 精度高.其旨在利用一阶导数信息, 解决最速下降法收敛时会产生收束震荡致使运算时间过长的问题, 又减少了牛顿法需要保存矩阵所占用的数据量以及矩阵求逆的运算量[.

将此方法引入OMP算法用以代替最小二乘法求解原始信号的估计值 x˙, 以期取得良好的图像重构效果.

改进的算法

输入 观测矩阵Φ, 观测向量y, 迭代次数为K;

输出 还原信号 x˙

Step 1 初始化 残差rt=y, 支撑集Λ, 候选集μ为空集, 迭代次数t=1;

Step 2 计算残差r与观察矩阵的列向量ϕ j内积除以列向量ϕ j的2范数, 记录其中的最大值最大的K个的索引, 即

λ t=arg maxj=1, 2,…,Nϕj2;

Step 3 更新候选集μ, 将选出的K个值对应的索引记入候选集, 使μ =μ t-1∪ {λ t}; 更新候选观察矩阵 Φλt=[ ϕλt]将内积最大值所对应观察矩阵列向量 ϕλt记入;

Step 4 运用共轭梯度法循化计算估计值 x˙, 初值为0, gn= ΦTλtΦλty, 步长

α n= ΦTλtΦλtrn-122,

计算并更新步长dn以及信号xk+1=xk+α kdk, 直至共轭梯度法迭代次数达到n( x˙的长度).

Step 5 计算估算值 x˙中所能引起残差变化最大的N个, 并将对应索引记入支撑集Λ .

W=arg min y-Φix˙i2, ∀ i=1, 2, …, K, 更新原子集Φ Λ=[ϕ Λ]将内积最大值所对应观察矩阵列向量记录;

Step 6 更新残差rn=rn-1-Φ Λ x˙Λ, 更新候选集μ =Φ Λ, 令迭代次数t+N;

判断 以t≥ K为停止条件, 如果条件不成立, 则返回执行Step 2, 若是条件成立, 则停止迭代并输出 x˙.

4 仿真实验

4.1 验证算法重构成功率

试验中以一维信号

x=sin(2π f1Tsts)+2sin(2π f2Tsts)+3sin(4π f3Tsts)+5sin(2π f4Tsts)

为分析范例.其中

f1=100Hz, f2=250Hz, f3=200Hz, f4=400Hz.采样频率fs=800Hz, 采样间隔ts=1/fs, 采样序列为1∶ 1024, 稀疏度为K=24.

定义重构成功率为η= 成功重构次数总测试次数.

OMP算法中理论上当采样次数M≥ K× log(N/K), 其中K是信号稀疏度, N为信号长度, 信号的重构成功率可以无限接近于1.当N=1024, K=24, M理论上约为40, 因此以高斯随机矩阵作为观察矩阵, 进行信号x的压缩采样使用OMP重构以及改进算法进行重构.验证采样数量M在低于40的情况下, 2种算法的重构成功率.

以重构后相对误差低于10-8为重构成功标准, 在每种采样值下进行1000次重复, 计算采样数量变化过程中的算法成功率.从图2中可以看出, 在使用相同的观察矩阵进行采样, 观测数低于40即低于理论重构采样数量下, 是改进算法成功率高于OMP算法, 随着采样数量增加到接近理论值时, 改进后的OMP算法与OMP算法的成功率基本相同.可见改进算法的可靠性基本与OMP算法相同, 近乎完全重构.

图2

Fig.2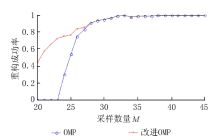图2 改进算法与OMP算法重构稳定性对比Fig.2 Comparison of reconstruction stability of the improved algorithm and OMP

4.2 图像信号仿真

图像信号仿真实验中选用灰度位图(像素256× 256)验证本文算法.此次进行的测试实验程序是在2.40GHz、6GB内存、采用Windows 7系统的计算机上运行, 在MATLAB 2010环境下进行操作.

对原始图像进行小波变换, 对在小波域上的稀疏信号, 使用高斯随机矩阵作为观测矩阵进行采样, 应用改进算法尝试还原原始图像, 并与其他重建算法还原图像进行对比试验说明.

图3

Fig.3图3 改进算法与其他算法重建效果对比Fig.3 Comparison of reconstruction effort of the improved algorithm and other algorithms

表1

Tab.1

表1(Tab.1)

表1 改进算法与其他算法重建时间对比Tab.1 Comparison of reconstruction time of the improved algorithm and other algorithms算法名称重构质量

(PSNR)重构时间/sOMP算法28.533832.1380

SP算法29.857438.1150

SAMP算法29.9574229.7800表1 改进算法与其他算法重建时间对比Tab.1 Comparison of reconstruction time of the improved algorithm and other algorithms

从图3和表1可以看出, 当采样率为 60%时, SAMP算法重构效果最好, 但由于使用步长逼近稀疏值, 在步长的计算与迭代中需要耗费大量时间.SP算法引入回溯思想用来选择最优原子集在提高重构精度的情况下, 算法计算的时间相对OMP算法也有所增加.而改进算法相比OMP算法由于在每次迭代中选出多个原子并且引入共轭梯度法从整体上进行信号估计, 用以代替最小二乘法.在明显减少算法收敛时间的同时取得了相对较好的图像重构效果.

5 结束语

本研究中, 利用基于OMP的改进算法, 实现了图像的重构.理论分析及实践仿真表明, 改进的OMP 算法能够有效缩减迭代收敛速度, 并保证还原精度.但是本文也存在不足之处, 由于共轭梯度算法更新方向并不一定是最优的, 会导致重构精度变化范围小, 一定程度上影响了压缩感知图像的重建质量, 下一步将针对更新方向上的局限性进行算法改进, 以期取得更好重建效果.

The authors have declared that no competing interests exist.

参考文献

[1]

CANDES E.Compressive sampling[C]. Proceedings of the International Congress of Mathematicians. Madrid Spain European Mathematicians Society Publishing House, 2006, 3: 1433-1452.

[本文引用:2]

[2]

BARANIUK R.A lecture compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.

[本文引用:3]

[3]

FANG H, YANG H R.Greedy algorithms and compressed sensing[J]. 2011, 37(12): 1413-1421.

[本文引用:2]

[4]

JUSTIN ROMBERG.Imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 14-20.

[本文引用:1]

[5]

DAVID DONOHO, YAAKOV TSAIG.Fast solution of ell-1-norm minimization problems when the solution may be sparse[R]. Stanford University Department of Statistics Technical Report, 2006.

[本文引用:1]

[6]

MÁRIO A T, FIGUEIREDO, ROBERT D, et al. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. 2007, 1(4): 586-598.

[本文引用:2]

[7]

TROPP J, GILBERT A C.Signal recovery from rand om measurements via orthogonal matching pursuit[J]. 2007, 53(12): 4655-4666.

[本文引用:3]

[8]

OSHER S, MAO Y, DONG B, et al.Fast linearized Bregman iteration for compressive sensing and sparse denoising[J]. 2010, 8(1): 93-111.

[本文引用:1]

[9]

张宗念, 黄仁泰, 闫敬文. 压缩感知信号盲稀疏度重构算法[J]. 电子学报, 2011, 39(1): 18-22.ZHANG Z N, HUANG R T, YAN J W.A blind sparsity reconstruction algorithm for compressed sensing signal[J]. 2011, 39(1): 18-22.

[本文引用:1]

[10]

ZAYYANI H, BABAIE-ZADEH M, JUTTEN C.Bayesian pursuit algorithm for sparse representation[C]. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, China;IEEE, 2009: 1549-1552.

[本文引用:1]

[11]

TROPP J, GILBERT A C.Signal recovery from rand om measurements via orthogonal matching pursuit[J]. 2007, 53(12): 4655-4666.

[本文引用:1]

[12]

SCHNELLE S R, LASLA J N, HEGDE C, et al.Texas HoId'Em algorithms for distributed compressive sensing[C]. 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), 2010: 2886-2889.

[本文引用:2]

[13]

KAREN E, ALESSANDRO F, VLADIMIR K.Compressed sensing image reconstruction via recursive spatially adaptive filtering[C]. IEEE International Conference on Image Processing, 2017: 549-552.

[本文引用:1]

[14]

欧庆波. 压缩感知在无线通信中的应用研究[D]. 南京: 南京邮电大学, 2011.OU Q B.The application of compressed sensing in wireless communication[D]. 2011.

[本文引用:2]

[15]

李志林. 图像压缩感知重建算法研究[D]. 北京: 北京交通大学, 2012.LI Z L.Study on image compressed sensing reconstruction algorithms[D].Beijing: Beijing Jiaotong University, 2012.

[本文引用:3]

[16]

BLUMENSATH T, DAVIES M E.Gradient pursuits[J]. 2008, 56(6): 2370-2382.

[本文引用:1]

[17]

HARMANY Z, THOMPSON D, WILLETT R, et al.Gradient projection for linearly constrained convex optimization in sparse signal recovery[C]. 2010 17th IEEE International Conference on Image Processing, 2010: 3361-3364.

[本文引用:3]

[18]

HESTENES M R, STIEFEL E L.Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Stand ards, 1952, 5(49): 409-436.

[本文引用:]

2

2006

0.0

0.0

... 压缩感知技术(compressed sensing,CS)是一种用于信号采样的新理论[1,2,3] ...

... 在压缩感知理论下,信号采样并不是直接测量信号本身,其关键在于梳理信息在信号中的结构与内容[1,2,4,5] ...

3

2007

0.0

0.0

... 压缩感知技术(compressed sensing,CS)是一种用于信号采样的新理论[1,2,3] ...

... 在压缩感知理论下,信号采样并不是直接测量信号本身,其关键在于梳理信息在信号中的结构与内容[1,2,4,5] ...

... x是存在多个解的,这是一个NP-hard问题[2] ...

2

2011

0.0

0.0

FANG H, YANG H R.Greedy algorithms and compressed sensing[J]. 2011, 37(12): 1413-1421.

Recently a family of iterative greedy algorithms have received extensive application in compressed sensing (CS) due to their fast reconstruction and low reconstruction complexity. In this paper, the basic theory of CS is first introduced and then we put emphasis on the main greedy algorithms for reconstruction, which include MP, OMP, IBOOMP, StOMP, SP, ROMP, CoSaMP and so on and provide their mathematical frameworks, respectively. Next, we classify all the algorithms according to the strategy of element selection and the update of the residual error. Under the condition of restricted isometry constant, further discussion on the performance of reconstruction algorithms such as running time, reconstruction stability and so on is presented. Last, the reconstruction results from simulated experiments further show the performance of all algorithms. And from those results we also acquire the relationship among the performance of the algorithms, the sparsity of signals to be reconstructed and the number of measurements, which lays a good basis for proposing new and better algorithms.

1. School of Science, Shanghai Second Polytechnic University, Shanghai 201209; 2. Department of Mathematics, Hefei Normal University, Hefei 230601

贪婪算法以其重建速度快、重建方法实现简便的特点在压缩感知(Compressed sensing, CS)理论中获得了广泛的应用. 本文首先介绍压缩感知的基本理论;然后,着重介绍现有几种重要的贪 婪重建算法,包括MP, OMP, IBOOMP, StOMP, SP, ROMP和CoSaMP等, 详细给出每种算法的数学框架和本质思想,着重从最优匹配原子的选择策略和残差信号的更新 方式这两个方面对各种算法进行对比分析,以限制等容常数为条件讨论各种算法在实现重建时的性能,包括重建时间、 重建的稳定性等;最后,通过模拟实验进一步验证了 各种算法的重建效果,同时模拟实验结果还进一步得出各种算法的重建效果与待重建信号 本身的稀疏度及测量次数这三者之间的关系,这也为新的更优算法的提出打下理论基础.

... 压缩感知技术(compressed sensing,CS)是一种用于信号采样的新理论[1,2,3] ...

... 而SP算法在重构过程中引入了回溯思想,既是使得选入信号支撑集的元素并非永久性保存,而是随着迭代的进行,对于支撑集中已经存在的原子进行再次计算,剔除其中非最优的原子,并且依据现在迭代环节加入最优原子,其目的在于以使局部最优解尽量接近于全局最优[3] ...

1

2008

0.0

0.0

... 在压缩感知理论下,信号采样并不是直接测量信号本身,其关键在于梳理信息在信号中的结构与内容[1,2,4,5] ...

1

2006

0.0

0.0

... 在压缩感知理论下,信号采样并不是直接测量信号本身,其关键在于梳理信息在信号中的结构与内容[1,2,4,5] ...

2

2007

0.0

0.0

... 压缩感知理论由Donoho和Candes等在2004年首次提出来,目前压缩感知理论的主要研究方向[6]分为信号稀疏性、测量矩阵和重构算法这3大部分 ...

... 其旨在利用一阶导数信息,解决最速下降法收敛时会产生收束震荡致使运算时间过长的问题,又减少了牛顿法需要保存矩阵所占用的数据量以及矩阵求逆的运算量[6,7] ...

3

2007

0.0

0.0

... 压缩感知中的采样过程相对简单,但重构非常复杂,所以对于重构算法的研究是压缩感知中相当重要的一方面[7] ...

... 最典型的贪婪算法是匹配追踪算法(Matching Pursuit),以及在其基础上改进的正交匹配追踪算法(Orthogonal Matching Pursuit)[7,8,9] ...

... 其旨在利用一阶导数信息,解决最速下降法收敛时会产生收束震荡致使运算时间过长的问题,又减少了牛顿法需要保存矩阵所占用的数据量以及矩阵求逆的运算量[6,7] ...

1

2010

0.0

0.0

... 最典型的贪婪算法是匹配追踪算法(Matching Pursuit),以及在其基础上改进的正交匹配追踪算法(Orthogonal Matching Pursuit)[7,8,9] ...

1

2011

0.0

0.0

张宗念, 黄仁泰, 闫敬文. 压缩感知信号盲稀疏度重构算法[J]. 电子学报, 2011, 39(1): 18-22.ZHANG Z N, HUANG R T, YAN J W.A blind sparsity reconstruction algorithm for compressed sensing signal[J]. 2011, 39(1): 18-22.

A new blind sparsity iterative greedy reconstruction algorithm is presented based on studying the signal reconstruction algorithm for compressed sensing without the prior information of signal sparsity.A stage-wised and backtracking method is employed to adaptively adjust the candidate list at each iteration in order to estimate the true supporting set of the approximated signal.The theoretical analysis and experiment simulation prove that the performance of the algorithm outperforms that of the existing state-of-art iterative greedy matching pursuit algorithms,and provides a generalized greedy reconstruction framework.The orthogonal matching pursuit and subspace pursuit can be viewed as its special case,and it also gives the best trade-offs between computational complexity and reconstruction performance.This makes it a promising candidate for many practical applications for compressed sensing signal reconstruction.

1. School of Electronics Engineering,Dongguan University of Technology,Dongguan,Guangdong 523106,China;2. School of Computer Science,Dongguan University of Technology,Dongguan,Guangdong 523106,China;3. Department of Electronics Engineering,Shantou University,Shantou,Guangdong 515063,China

研究压缩感知信号重构算法,提出了一种不需要精确知道信号稀疏度的先验知识,就能重构出目标信号的盲稀疏度迭代贪婪跟踪重构新算法.采用分段的方法来逐段估计、扩充目标信号的真实支撑域,并应用后向追踪思想,自适应地调整候选序列,以便每一次迭代时更加精确地估计真正的支撑域.理论分析与实验证明,算法性能超过了现有的迭代贪婪跟踪重构算法性能;给出了迭代贪婪跟踪信号重构的统一框架,正交匹配跟踪和子空间跟踪算法可以看成它的特例;在计算复杂度和重构算法性能之间做出了最佳折衷;有更强的实用性.

... 最典型的贪婪算法是匹配追踪算法(Matching Pursuit),以及在其基础上改进的正交匹配追踪算法(Orthogonal Matching Pursuit)[7,8,9] ...

1

2009

0.0

0.0

... x求解问题[10,11,12,13],是重构算法研究中的重要方向之一 ...

1

2007

0.0

0.0

... x求解问题[10,11,12,13],是重构算法研究中的重要方向之一 ...

2

2010

0.0

0.0

... x求解问题[10,11,12,13],是重构算法研究中的重要方向之一 ...

... 另一种是贪婪类算法,以MP(匹配追踪算法)、OMP(正交匹配追踪算法)为典型代表,是目前应用非常广泛的一类[12] ...

1

2017

0.0

0.0

... x求解问题[10,11,12,13],是重构算法研究中的重要方向之一 ...

2

2011

0.0

0.0

欧庆波. 压缩感知在无线通信中的应用研究[D]. 南京: 南京邮电大学, 2011.OU Q B.The application of compressed sensing in wireless communication[D]. 2011.

... 同时通过对已选原子集的正交投影化改进MP算法迭代选择中出现的次优问题[14,15,16,17] ...

... 3 针对OMP算法的改进OMP算法在计算中需要使用最小二乘法进行测量信号的计算,但最小二乘法本质上是求解样本观测值与估计值的残差平方和最小的极值问题的一种方法,在非经典线性问题求解上精度并不高,使得信号重构过程中残差更新的误差逐渐积累,降低重构质量[14,15]因此针对此问题,结合子空间追踪(SP)算法的#cod#x0201c ...

3

2012

0.0

0.0

... 同时通过对已选原子集的正交投影化改进MP算法迭代选择中出现的次优问题[14,15,16,17] ...

... 3 针对OMP算法的改进OMP算法在计算中需要使用最小二乘法进行测量信号的计算,但最小二乘法本质上是求解样本观测值与估计值的残差平方和最小的极值问题的一种方法,在非经典线性问题求解上精度并不高,使得信号重构过程中残差更新的误差逐渐积累,降低重构质量[14,15]因此针对此问题,结合子空间追踪(SP)算法的#cod#x0201c ...

... 1 共轭梯度下降算法共轭梯度法(conjugate gradient method,CG),最初是为求解正定系数矩阵线性方程组而提出的[15] ...

1

2008

0.0

0.0

... 同时通过对已选原子集的正交投影化改进MP算法迭代选择中出现的次优问题[14,15,16,17] ...

3

2010

0.0

0.0

... 同时通过对已选原子集的正交投影化改进MP算法迭代选择中出现的次优问题[14,15,16,17] ...

... 共轭梯度法作为典型的共轭方向法,其任意搜索方向是互相共轭的[17,18] ...

... Rn,A是对称正定矩阵[17] ...

1952