差分进化算法——4

1、题目

2、仿真过程

3、代码实现

4、结果

1、例题：用离散差分进化算法求函数的最大值，其中x的取值范围为-100~100之间的整数，y的取值范围-100~100之间的整数。其函数值图形如图所示

2、仿真过程

(1)初始化个体数目为NP=20，变量维数为D=2，最大进化代数G=100,初始变异算子F=0.5,

交叉算子CR=0.1.

(2)产生数值为【-100，100】内整数的初始种群，计算个体目标函数值；进行变异操作，对交叉后的种群内数值进行取整操作，然后进行交叉操作、边界条件处理，产生临时种群，其中边界条件处理采用在边界吸收方式。

（3）计算临时种群个体目标函数，与原种群对应个体进行“一对一”选择操作，产生新种群。

（4）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值，若不满足，则继续进行迭代优化。

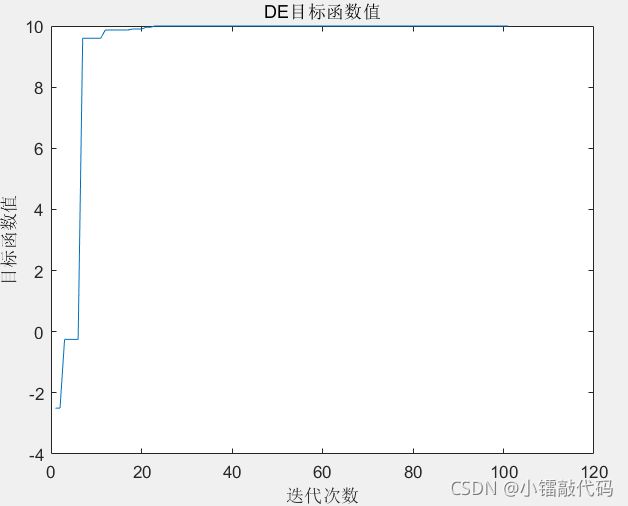
优化结束后，DE目标函数进化曲线如图所示，优化后的结果为

x=-2,y=-3,函数最大值 f(x,y)= 10

3、代码实现

  3.1——图像代码

clear all;
close all;
clc;
x=-100:1:100;
y=-100:1:100;
N=size(x,2);
for i=1:N
    for j=1:N
        z(i,j)=-((x(i)^2+y(j)-1).^2+(x(i)+y(j)^2-7).^2)/200+10;
    end
end
mesh(x,y,z)
xlabel('x')
ylabel('y')

 3.2——DE代码实现

%%%% 差分进化算法求函数极值 %%%%
%% 初始化
clear all;
close all;
clc;
NP=20;    % 种群数量
D=2;     % 变量的维数
G=100;    % 最大进化代数
F0=0.5;   % 初始变异算子
CR=0.1;   % 交叉算子
Xs=100;    % 上限
Xx=-100;   % 下限

%% 赋初值
x = zeros(D,NP);   %初始化种群
v = zeros(D,NP);   %变异种群
u = zeros(D,NP);   %选择种群
x=randi([Xx,Xs],D,NP);  %赋初值

%% 计算目标函数
for m = 1:NP
    Ob(m)=func3(x(:,m));
end
trace(1) = max(Ob);

%% 差分进化循环
for gen=1:G
     %变异操作
     %自适应变异算子
     lamda = exp(1-G/(G+1-gen));   
     F = F0*2^(lamda);
     % r1,r2,r3和m互不相同
     for m =1:NP
         r1 = randi([1,NP],1,1);
         while(r1==m)
             r1 =randi([1,NP],1,1);
         end
         r2 = randi([1,NP],1,1);
         while (r2==m)|(r2==r1)
             r2=randi([1,NP],1,1);
         end
         r3 = randi([1,NP],1,1);
         while (r3==m)|(r3==r2)|(r3==r1)
             r3 =randi([1,NP],1,1);
         end
         v(:,m) = floor(x(:,r1)+F*(x(:,r2)-x(:,r3)));   % floor向下取整
     end
     
     % 交叉操作
     r = randi([1,D],1,1);
     for n = 1:D
         cr = rand(1);
         if(cr<=CR)|(n==r)
             u(n,:)=v(n,:);
         else
             u(n,:)=x(n,:);
         end
     end
     
     %% 边界条件的处理
     % 边界吸收
     for  n=1:D
         for m=1:NP
             if u(n,m)Xs
                 u(n,m)=Xs;
             end
         end
     end
     
     % 选择操作
     for m=1:NP
         Ob1(m)=func3(u(:,m));
     end
     for m=1:NP
         if Ob1(m)>Ob(m)
             x(:,m)=u(:,m);
         end
     end
     for m =1:NP
         Ob(m) = func3(x(:,m));
     end
     trace(gen+1)=max(Ob);
end

[SortOb,Index] = sort(Ob);
x= x(:,Index);
X = x(:,1)    % 最优变量
Y = max(Ob)   % 最优值

%% 画图
figure
plot(trace);
xlabel('迭代次数')
ylabel('目标函数值')
title('DE目标函数值')

 

%% 适应度函数
function y = func3(x)
y=-((x(1)^2+x(2)-1).^2+(x(1)+x(2).^2-7).^2)/200+10;

4、结果展示

   4.1——函数图像展示

  4.2——DE目标函数曲线