机器学习入门:隐马尔科夫模型-8
机器学习入门:隐马尔科夫模型
1、实验描述
-
本实验先简单介绍隐马尔科夫模型,然后提供一份股票交易的数据,通过建立隐马尔科夫模型对股票数据进行分析,并将最终结果用图的方式展示出来。
-
实验时长:45分钟
-
主要步骤:
-
读取数据文件
-
数据预处理
-
模型创建
-
模型的预测
-
模型评估
-
绘制相关的指标
-
2、实验环境
- 虚拟机数量:1
- 系统版本:CentOS 7.5
- scikit-learn版本: 0.19.2
- numpy版本:1.15.1
- matplotlib版本:2.2.3
- python版本:3.5
- IPython版本:6.5.0
- hmmlearn版本:0.2.0
3、相关技能
-
Python编程
-
Scikit-learn编程
-
Matplotlib编程
-
Numpy编程
-
隐马尔科夫模型
4、相关知识点
- 隐马尔科夫模型
- 模型建立
- 模型预测
- 模型评估
- 状态序列
- 观测序列
5、实现效果
6、实验步骤
6.1隐马尔科夫模型:HMM(Hidden Markov Model)是关于时序的概率模型,描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列,再由各个状态生成观测随机序列的过程。隐马尔科夫模型随机生成的状态随机序列,称为状态序列;每个状态生成一个观测,由此产生的观测随机序列,称为观测序列。序列的每个位置可以看做是一个时刻。
6.1.1隐马尔科夫模型三个基本问题:
6.1.1.1概率计算问题: 给定模型和观测序列 ,计算模型λ下观测序列O出现的概率P(O| λ)
6.1.1.2学习问题: 已知观测序列,估计模型的参数,使得在该模型下观测序列P(O| λ)最大
6.1.1.3预测问题:解码问题:已知模型和观测序列,求给定观测序列条件概率P(I|O,λ)最大的状态序列I
6.2.进入Anaconda创建的虚拟环境“ML” ,并准备相应的数据文件。
6.2.1.从zkpk的公共目录下拷贝实验所需的数据文件到zkpk的家目录下
[zkpk@master ~]$ cd
[zkpk@master ~]$ cp /home/zkpk/experiment/SH600000.txt /home/zkpk
6.2.1.1数据集SH600000.txt介绍:
6.2.1.2数据共1511行7列,每一行为一个股票交易相关的指标
6.2.1.3每列分别代表:日期、开盘、最高价、最低价、收盘、成交量、成交额
6.2.2在zkpk的家目录下执行如下命令
[zkpk@master ~]$ cd
[zkpk@master ~]$ source activate ML
(ML) [zkpk@ master ML]$
6.2.3此时已经进入虚拟环境。键入如下命令,进入ipython交互是编程环境
(ML) [zkpk@ master ML]$ ipython
Python 3.5.4 |Anaconda, Inc.| (default, Nov 3 2017, 20:01:27)
Type 'copyright', 'credits' or 'license' for more information
IPython 6.2.1 -- An enhanced Interactive Python. Type '?' for help.
In [1]:
6.3在Ipython交互式编程环境中开始进行实验
6.3.1导入实验所需的包
In [1]: import numpy as np
...: from hmmlearn import hmm
...: import matplotlib.pyplot as plt
...: import matplotlib as mpl
...: from sklearn.metrics.pairwise import pairwise_distances_argmin
...: import warnings
6.3.2读取数据文件
6.3.2.1使用“\t”分割符切词, 跳过前两行,抽取指定的列
In [2]: x = np.loadtxt('SH600000.txt', delimiter='\t', skiprows=2, usecols=(4, 5, 6, 2, 3)) # 列(4, 5, 6, 2, 3)分别对应数据集中的收盘价、成交量、成交额、最高、最低的数据
6.3.3数据预处理
6.3.3.1读取对应的字段
In [6]: close_price = x[:, 0] #收盘价
...: volumn = x[:, 1] #交易量
...: amount = x[:, 2] #交易额
6.3.3.2计算振幅:每天的最高价与最低价的差
In [7]: amplitude_price = x[:, 3] - x[:, 4] # 振幅:每天的最高价与最低价的差
In [8]: diff_price = np.diff(close_price) # 涨跌值:收盘后价格做一个一阶差分;即今日收盘价减去昨日收盘价
6.3.3.3所有元素跳过第一个元素
In [10]:volumn = volumn[1:] # 成交量
...: amount = amount[1:] # 成交额
...: amplitude_price = amplitude_price[1:] # 每日振幅
6.3.3.4将多个特征叠加起来,形成样本。
In[11]: sample = np.column_stack((diff_price, volumn, amount, amplitude_price)) # 观测值;column_stack利用1-D数组组成的序列,生成一个2-D数组,其中每个1-D数组依次作为结果2维数组中的列
6.3.4建立模型:训练数据只有观测序列,则HMM的学习需要使用EM算法,是非监督学习
In [12]: n = 5 #给定五个类别(状态)
...: model = hmm.GaussianHMM(n_components=n, covariance_type='full') # 建立模型
#指定每个类别的系数:方差各不相同。
6.3.5利用样本进行模型训练
In [13]:model.fit(sample) # 训练模型
6.3.6模型预测:
6.3.6.1输出每个类别的相应概率值
6.3.6.2设置浮点输出,以及每个维度的输出个数
In [15]: y = model.predict_proba(sample) # 输出类别的概率值
...: np.set_printoptions(suppress=True, edgeitems=100)
...: print('proba:\n', y)
6.3.7绘制跌涨值,交易量,所有组分,组分概率的图示
In [16]: t=np.arange(len(diff_price))#跌涨值的length作为时间维度的长度
...: plt.figure(figsize=(10,6.7), facecolor='w') #设置图示中画布的整体大小及背影色
...: plt.subplot(421) # 子图的布局,4行两列
...: plt.plot(t, diff_price, 'r-')
...: plt.grid(True)
...: plt.title('amplitude_price') #每日振幅
...: plt.subplot(422)
...: plt.plot(t, volumn, 'g-') # 交易量
...: plt.grid(True)
...: plt.title('volumn')
...: clrs = plt.cm.terrain(np.linspace(0, 0.8, n)) # linspace方法在指定范围内返回均匀间隔的数字;
...: plt.subplot(423)
...: for i, clr in enumerate(clrs):
...: plt.plot(t, y[:, i], '-', lw=0.3, color=clr, alpha=0.7)
...: plt.title('All components') # 所有组分
...: plt.grid(True)
...: for i, clr in enumerate(clrs):
...: axes = plt.subplot(4,2,i+4)
...: plt.plot(t, y[:,i], '-', color=clr)
...: print('Component probability ', y[:,i]) #组分概率
...: plt.grid(True)
...: plt.title("Compoent %d" %(i+1))
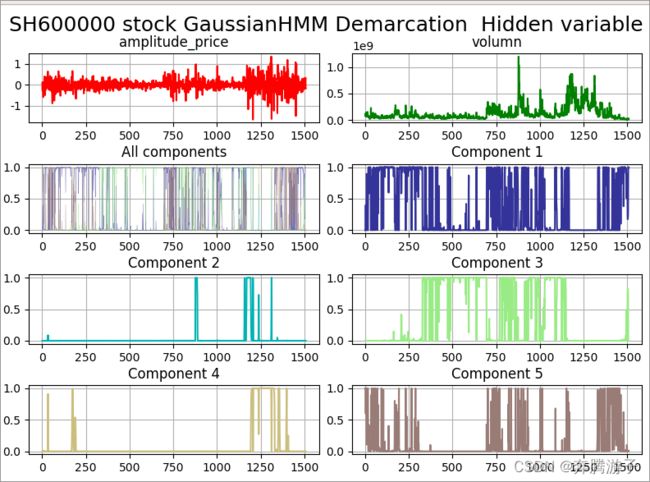
In [18]: plt.suptitle('SH600000 stock GaussianHMM Demarcation Hidden Variable')
In [20]: plt.tight_layout()
In [21]: plt.subplots_adjust(top=0.8)
In [22]: plt.show()
7、参考答案
- 代码清单Hmm_test.py
8、总结
本次实验使用隐马尔科夫模型,对股票数据进行分析,大体流程是数据预处理、建模、训练模型、预测及最终结果可视化。涉及的理论及编码知识量较大,需要大家多多理解相关的理论知识,在此基础上进行相应的编程实现。在编程的过程中,要学会查阅文档的方式解决疑问,如类、方法如何使用、作用是什么、某参数的意思是什么等等问题。