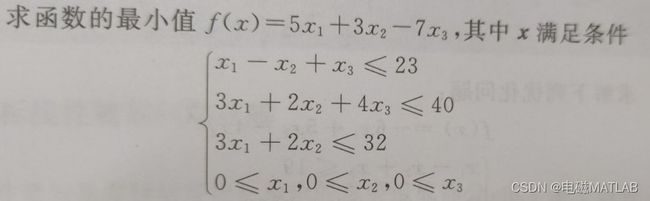基于鸽群优化算法的线性规划求解matlab程序
1 鸽群算法
鸽群作为一种鸟群,拥有着卓越的导航能力和长距离飞行的能力,同时,鸽群内的个体还能通过彼此互相的学习、记忆来进行飞行状态的迭代更新,从而进行十分稳定的群体飞行,鸽群的这种优秀的对于环境的识别能力和导航能力成为了国内外众多学者的研究对象。上世纪初,相关学者对于旅行鸽能够准确的回到巢穴的行为展开了研究,并指出,鸽群能够借助当地的地磁与地标信息来对自身的位置进行定位与更新,从而能够辨别方向找到巢穴所在。

经典鸽群算法(pigeon-inspired optimization,PIO)由段海滨等人于2014年提出,该算法由地磁单元和地标单元两个导航单元构成,通过地磁单元和地标单元两个独立的阶段模拟鸽群进行速度和位置更新的导航机制,鸽群在地磁单元阶段根据当地磁场和太阳的高度来判别自身的位置,并进行速度的更新;在地标单元阶段由当地的地标信息来辨别自身的位置与速度。在这两个阶段分别用到不同的算子模型,在地磁单元阶段存在地图和指南针算子,在地标阶段存在地标算子:
(1)地磁单元阶段
在地磁单元阶段,鸽子根据对于当地磁场等物质进行判断,同时在脑海中规划出飞行路线,并能够根据当地太阳的高度来对自身的方向进行实时调整,这种对地磁信息的依赖性会随着鸽群靠近目标点而逐渐减弱。
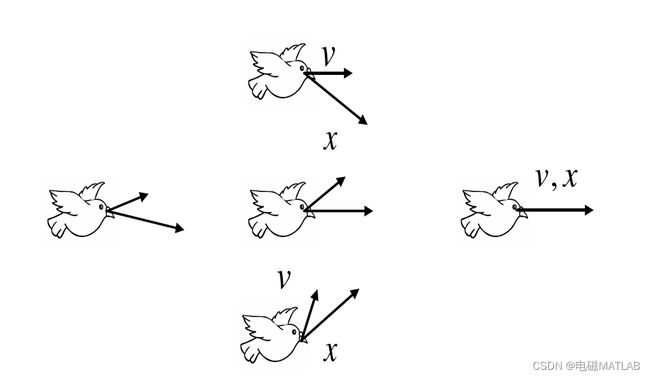
(2)地标单元阶段
鸽子的记忆能力很强,能够对周围的地标信息迅速记忆,当距离目标点比较近时,鸽子会参考当地的地标在脑海中勾勒出地图并根据地标进行位置与速度的调整,直到抵达目标点。如果某只鸽子对当地的地标不熟悉,鸽子也会根据周围对地标熟悉的鸽子的飞行状态对自身飞行进行调整。在每一次迭代的过程中,会根据每只鸽子的适应度的不同进行淘汰,淘汰适应度较差的一半鸽子,计算剩余适应度较优的鸽子的中心位置,并作为种群中的参考方向。
PIO算法也是一种群体算法,对于个体进行随机初始化,空间中的每一个个体都代表着一个可行解,然后通过两个阶段的寻优搜索。在地磁单元阶段寻优的过程中间,PIO算法会对整个群体中的最优解进行保留,然后进行个体速度与位置的迭代更新,对解空间进行充分的搜索,具有快速性与随机性,使得搜索的效率较高,种群的多样性较好。在经过地磁阶段的搜索以后,进入地标单元阶段,鸽群会逐渐向一个位置较优的领导鸽进行靠近,这个阶段过程缓慢,搜索比较仔细,范围比较局部,能够较为精确的对搜索种群的最优值。

3 鸽群算法求解结果
迭代曲线
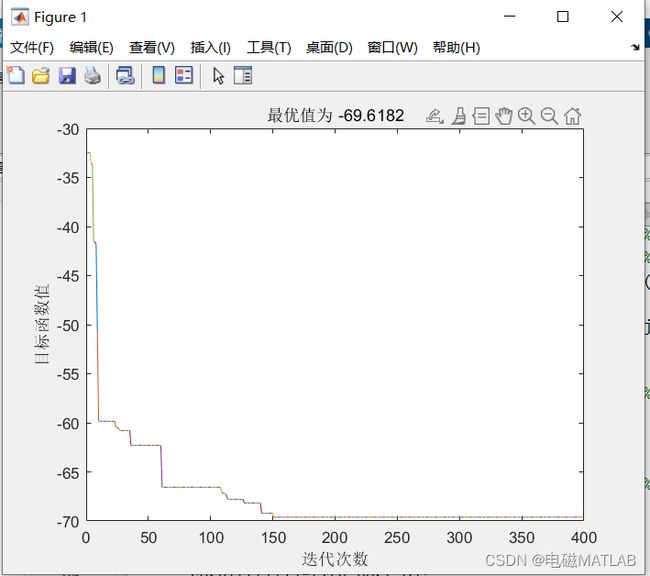
4 matlab程序
1)主函数
clear
clc
close all
format long;
T1=200; %Global search algebra
T2=200; %Local search algebra
pigeonnum=500; %number
D = 30; % dimensionality
R=0.3; %parameters of magnetic field
bound=[0,15]; %hunting zone
tol = 1e-7;
f1=@fitness;
%**************initialization of the individual pigeon************
for i=1:pigeonnum %时间复杂度O(pigeonum*D*2)
for j=1:D
x(i,j)=bound(1)+rand*(bound(2)-bound(1));
v(i,j)=rand;
end
end
%**************calculate the fitness of pigeon***********
for i=1:pigeonnum %时间复杂度O(pigeonum*2)
p(i)=f1(x(i,:),D);
p_best(i,:)=x(i,:);
end
%**************find the optimal pigeons********************
g_best=x(1,:);
for i=2:pigeonnum %时间复杂度O(pigeonum-1)
if f1(g_best,D)>f1(x(i,:),D)
g_best=x(i,:);
end
end
%************ magnetic compass and solar operator********************
for t=1:T1 %时间复杂度O(T1*(pigeonum*(2D+5))+1)
for i=1:pigeonnum %时间复杂度O(pigeonum*(2D+5))
v(i,:)=v(i,:)+rand*(p_best(i,:)-x(i,:));
x(i,:)=x(i,:)*(1-exp(-R*t))+v(i,:); %check whether beyond the searching space
for j=1:D % magnetic field and solar operator
if abs(i-1)<=eps
if x(i,j)bound(2)
x(i,j)=bound(1)+rand*(bound(2)-bound(1));
v(i,j)=rand;
end
else
if x(i,j)bound(2)
x(i,j)=x(i-1,j);
v(i,j)=v(i-1,j);
end
end
end
if f1(x(i,:),D)f1(x(j,:),D)
temp_pigeon=x(i,:);
x(i,:)=x(j,:);
x(j,:)=temp_pigeon;
end
end
end
pigeonnum=ceil(pigeonnum/2); %remove half of the pigeons according to the landmark
addpigeonnum=0;
for i=1:pigeonnum
addpigeonnum=addpigeonnum+x(i,:);
p(i)=f1(x(i,:),D); %calculate fitness and location of the pigeon after sorting
p_best(i,:)=x(i,:);
end
pigeoncenter=ceil(addpigeonnum./pigeonnum);%calculate central position
for i=1:pigeonnum %local searching
for j=1:D %check whether beyond the searching space
x(i,j) = x(i,j) + rand*(pigeoncenter(j)-x(i,j));
while x(i,j)bound(2)
x(i,j) = x(i,j) + rand*(pigeoncenter(j)-x(i,j));
end
end
if f1(x(i,:),D)