实测:nn.CrossEntropyLoss()多维输出 + 权重分配
pytorch版本:1.10.0
part1:多维输出部分
问题描述:
我有长度为14万的频域序列数据若干,要对每条序列进行异常检测。我将每个长序列划分为多个短序列,每个短序列长度为1000,即140000 = 140×1000,Model输出是140个值,即将序列检测问题转换为时间序列分类问题。
因此,我的模型输出(输入给loss函数)为16×140×2,对140个短序列作二分类,loss使用nn.CrossEntropyLoss(),多维输出。
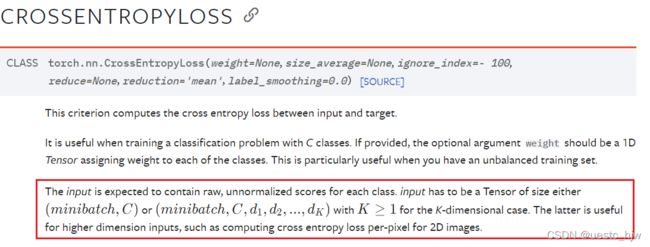
官方文档定义为:
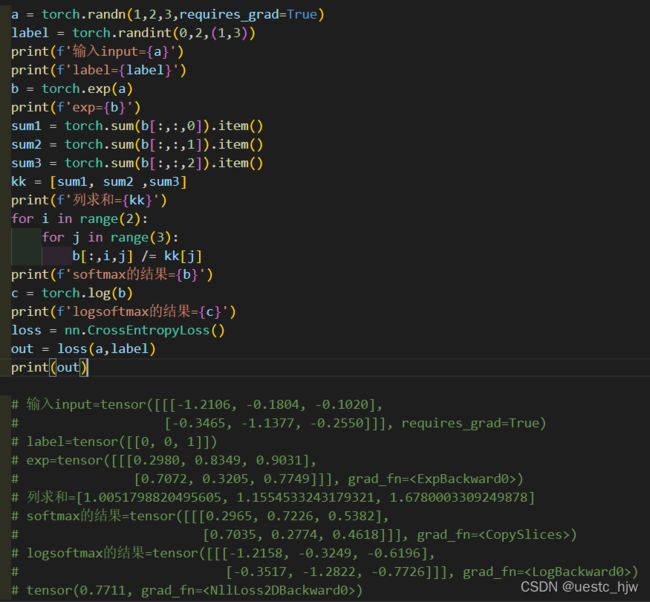
为简单起见,我的测试代码如下所示:
输入input维度:[1,2,3]
标签label维度:[1,3]
输出output维度:1个值,是3维的平均值(在weight默认,reduction默认为'mean'时),即 0.7711 = - [ -1.2158 - 0.3249 - 0.7726] / 3
part2:权重分配部分
主要是用来解决类别不平衡问题。在我的实际问题中,正反类数量为3:137,严重不平衡。
在这里解释一下如何设置权重。
结论是:为数量少的类别设置更大的权重。
原因:对于二分类问题,模型会犯2种错误,即①将正类预测为反类②将反类预测为正类
在我的Dataset中,正类极少,因此学习到的Model会更倾向于预测为反类,因此我要惩罚第①种错误,避免都预测为反类。
2022.3.7 更新:
上面对于权重分配方面,是我一厢情愿了,真实测试发现,pytorch并不是这样理解权重分配的。
nn.CrossEntropyLoss()里面的权重,作用是平衡正反类样本的数量。
因此,可以理解权重是将该样本(也就是该类样本)的数量增加m倍。
Pytorch中nn.CrossEntropyLoss()加权计算方式如下:
注:以下内容请对应nn.CrossEntropyLoss()pytorch的官方文档阅读。
若batch_size>1,那么nn.CrossEntropyLoss()输出结果已经平均掉batch_size = N了
程序验证:
a = torch.tensor([[-0.4514,0.7823,0.5210],[-0.0082,-0.3569,-0.2626]],requires_grad=True)
a = a.unsqueeze(0)
tar = torch.tensor([[0,1,1]])
# a = torch.randn(1,2,3,requires_grad=True)
# tar =torch.randint(0,2,(1,3))
# print(a,'\n',tar)
fn1 = nn.CrossEntropyLoss(reduction='mean')
fn2 = nn.CrossEntropyLoss(reduction='sum')
# 加权后
fn3 = nn.CrossEntropyLoss(weight=torch.tensor([1.,5.]),reduction='mean')
fn4 = nn.CrossEntropyLoss(weight=torch.tensor([1.,5.]),reduction='sum')
loss1 = fn1(a,tar)
loss2 = fn2(a,tar)
print(f'mean_loss = {loss1}, sum_loss = {loss2} , 3*mean_loss = {3*loss1}')
loss3 = fn3(a,tar)
loss4 = fn4(a,tar)
print(f'mean_loss = {loss3}, sum_loss = {loss4} , 11*mean_loss = {11*loss3}')
''' 输出结果是: '''
# mean_loss = 1.1719348430633545, sum_loss = 3.5158045291900635 , 3*mean_loss = 3.5158045291900635
# mean_loss = 1.2566012144088745, sum_loss = 13.822613716125488 , 11*mean_loss = 13.822613716125488发现和自己手算的结果是一致的:
a = torch.tensor([[-0.4514,0.7823,0.5210],[-0.0082,-0.3569,-0.2626]],requires_grad=True)
a = a.unsqueeze(0)
p = exp(-0.4514)/(exp(-0.4514)+exp(-0.0082))
q = exp(0.7823)/(exp(0.7823)+exp(-0.3569))
f = exp(0.5210)/(exp(0.5210)+exp(-0.2626))
sof = torch.tensor([[p,q,f],[1-p,1-q,1-f]])
pp = -log(0.3910)-5*log(0.2425)-5*log(0.3135)
print(pp)
print(pp/11)
# 13.822595156565576
# 1.2565995596877797