python最小二乘法--拟合直线
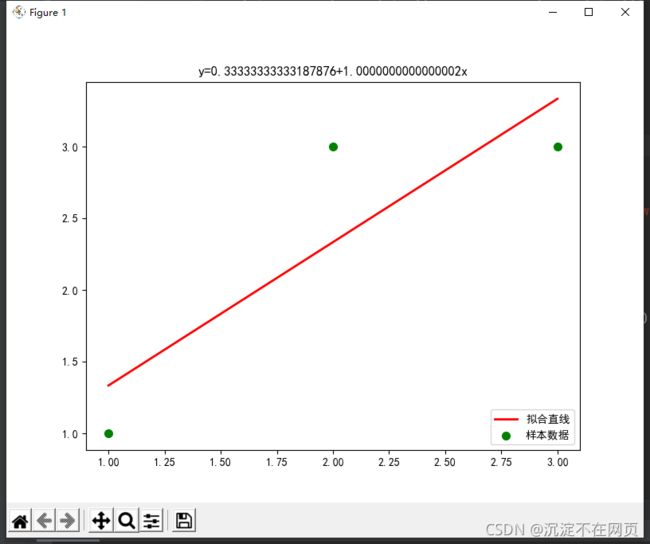
最小二乘法实例------求出利用最小二乘法通过(1,1) (2,3) (3,3)拟合出的直线:
##最小二乘法
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
plt.rcParams['font.sans-serif']=['SimHei']
Xi = np.array([1,2,3])
Yi = np.array([1,3,3])
def func(p, x):
k, b = p
return k * x + b
def error(p, x, y):
return func(p, x) - y
p0 = [1, 1]
Para = leastsq(error, p0, args=(Xi, Yi))
k, b = Para[0]
print("k=", k, "b=", b)
print("cost:" + str(Para[1]))
print("求解的拟合直线为:")
print("y=" + str(round(k, 2)) + "x+" + str(round(b, 2)))
plt.figure(figsize=(8, 6))
plt.scatter(Xi, Yi, color="green", label="样本数据", linewidth=2)
x = np.array([1,2,3])
y = k * x + b
plt.plot(x, y, color="red", label="拟合直线", linewidth=2)
plt.title('y={}+{}x'.format(b,k))
plt.legend(loc='lower right')
plt.show()
最小二乘法原理:
求使得目标函数(损失函数)最小化时的拟合函数模型,即求使得目标函数最小化时的拟合函数的参数。
给定假设拟合函数,给定样本,目标函数即为样本值减去带入假设拟合函数的理论值的平方再求和。
plt.scatter():散点图用法
plt.scatter(x,y,s=None,c=None,marker=None,alpha=None.linewidths=None,edgecolors=None,**kwargs)
x,y:表示绘制散点图的数据点的横纵坐标;s:实数,表示数据点区域大小,可选;c:表示颜色,默认为蓝色,可选;marker:表示标记样式,默认为‘o’;alpha:0-1之间的实数,颜色深度;linewidths:标记点长度。
scipy.optimize.leastsq():最小二乘法
参数很多,一般我们只需要前三个就可以了。func:目标函数;x0:待定参数的初始值;args():函数的其他参数,一般为数据点。
注意: 添加中文时需要加上一句代码否则会乱码。
plt.rcParams['font.sans-serif']=['SimHei'] #添加中文plt.legend(labels,loc):
labels是图例名称(曲线名称),没有设置的话,默认为plt.plot()中label的值,也是图例名称,plt.legend()只是使该图例名称生效。
loc表示图例在坐标轴中的位置,一般选取"best"。