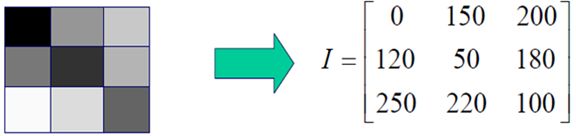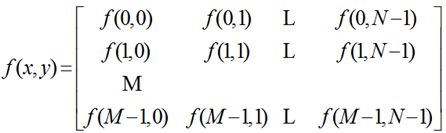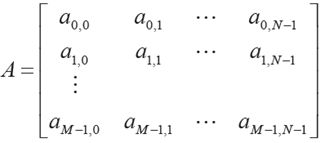1. 取样和量化的基本概念(Concepts)
获取图像的目标是从感知的数据中产生数字图像,但是传感器的输出是连续的电压波形,因此需要把连续的感知数据转换为数字形式。这一过程由图像的取样与量化来完成。 数字化坐标值称为取样;数字化幅度值称为量化。
图像采样
◆ 在取样时,若横向的像素数(列数)为M ,纵向的像素数(行数)为N,则图像总像素数为M*N个像素。
◆ 一般来说,采样间隔越大,所得图像像素数越少,空间分辨率低,质量差,严重时出现马赛克效应;采样间隔越小,所得图像像素数越多,空间分辨率高,图像质量好,但数据量大。
图像的量化
◆ 量化等级越多,所得图像层次越丰富,灰度分辨率高,图像质量好,但数据量大;量化等级越少,图像层次欠丰富,灰度分辨率低,会出现假轮廓现象,图像质量变差,但数据量小.
很明显,数字图像的质量在很大程度上取决于取样和量化中所用的样本数和灰度级。一般,当限定数字图像的大小时, 为了得到质量较好的图像可采用如下原则:
(1) 对缓变的图像, 应该细量化, 粗采样, 以避免假轮廓。
(2) 对细节丰富的图像,应细采样,粗量化, 以避免模糊(混叠)。
2. 数字图像描述
黑白图像
指图像的每个像素只能是黑或者白,没有中间的过渡,故又称为2值图像。2值图像的像素值为0、1。
灰度图像
灰度图像是指每个像素的信息由一个量化的灰度级来描述的图像,没有彩色信息。
彩色图像
彩色图像是指每个像素的信息由RGB三原色构成的图像,其中RBG是由不同的灰度级来描述的。
3. 图像的数字表示
令f(s, t)表示一幅具有两个连续变量s和t的连续图像函数。通过取样和量化, 我们可把该函数转换为数字图像。将该连续图像取样为一个二维阵列f(x,y), 该阵列有M行和N列,其中(x,y)是离散坐标。
在某些讨论中,使用传统的矩阵表示法来表示数字图像及其像素更为方便:
二维矩阵是表示数字图像的重要数学形式。一幅M×N的图像可以表示为矩阵:矩阵中的每个元素称为图像的“像素”。每个像素都有它自己的“位置”和“值”,“值”是这一“位置”像素的颜色或者强度。
假定图像尺寸为M、N,每个像素所具有的离散灰度级数为G;这些量分别取为2的整数幂m,n,k,即M=2m, N=2n,G=2k 则存储这幅图像所需的位数是:;如果图像是正方形,即M=N,当一副图像有灰度级时,实际上通常称该图像为k比特图像。如,一幅图像有256可能的灰度级称为8比特图像。