线性回归（Linear Regression）

1 概述

  线性回归（Linear Regression）是一种通过属性的线性组合来进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。

2 单变量线性回归

  在初中时，我们知道线性函数$y=kx+b$

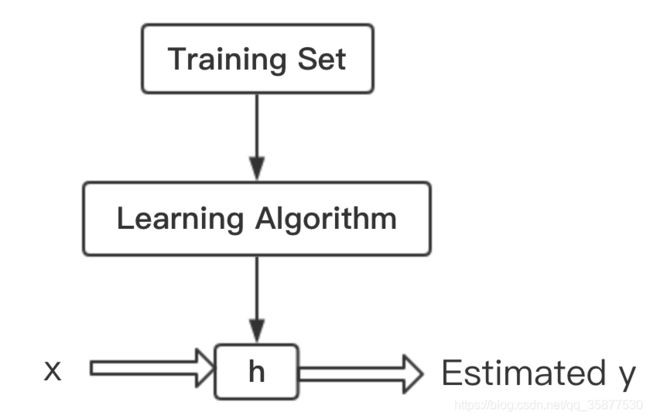
  单变量线性回归模型$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$，${\theta }_0,{\theta }_1$被称为模型参数。如果我们知道${\theta }_0,{\theta }_1$，就能对任意的$x$进行预测了。任何机器学习过程如下图所示：

  代价函数：
$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
  目标就是最小化代价函数：$minJ({\theta }_0,{\theta }_1)$
  下面是代价函数$J({\theta }_0,{\theta }_1)$与${\theta }_0,{\theta }_1$之间的关系


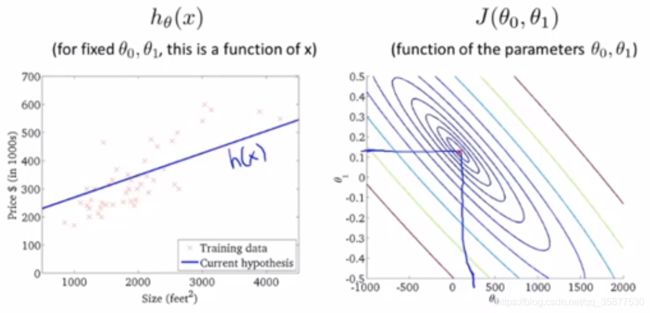
  从图中可以看出，当${\theta }_0,{\theta }_1$处于代价函数的最小值时，得到最优的拟合结果。
  求代价函数$J({\theta }_0,{\theta }_1)$的最小值，可以有两种方法：
1 最小二乘法：
  针对单变量线性回归，具有线性关系，为了获得代价函数$J({\theta }_0,{\theta }_1)$的最小值，可以利用$J({\theta }_0,{\theta }_1)$分别对${\theta }_0,{\theta }_1$求导，令其导数为0，然后再得到${\theta }_0,{\theta }_1$的值，根据导数的性质，此时得到的${\theta }_0,{\theta }_1$就是模型的最优值。
$\{\begin{array}{c}\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\Sigma }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})=\frac{1}{m}{\Sigma }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})=0\\ \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\Sigma }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}=\frac{1}{m}{\Sigma }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})x^{(i)}=0\end{array}$

${\theta }_0=\frac{{\Sigma }_{i=1}^m(x^{(i)}{)}^2{\Sigma }_{i=1}^m{y}^{(i)}-{\Sigma }_{i=1}^m{x}^{(i)}{\Sigma }_{i=1}^m{x}^{(i)}{y}^{(i)}}{m{\Sigma }_{i=1}^m(x^{(i)}{)}^2-({\Sigma }_{i=1}^m{x}^{(i)}{)}^2}$

${\theta }_1=\frac{m{\Sigma }_{i=1}^m{x}^{(i)}{y}^{(i)}-{\Sigma }_{i=1}^m{x}^{(i)}{\Sigma }_{i=1}^m{y}^{(i)}}{m{\Sigma }_{i=1}^m(x^{(i)}{)}^2-({\Sigma }_{i=1}^m{x}^{(i)}{)}^2}$

  这就是最小二乘法的解法，就是求得损失函数的极值点。
2 梯度下降法（Gradient Descent Algorithm）：
  如下图所示，就好比一个人站在山上，想走到山谷的位置，每一步沿着山体梯度的方向往下走，无疑是最快的方向。

${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$(for $j=0,1$)
$\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\Sigma }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$
$\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}{\Sigma }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$

  $\alpha$叫做学习率，当$\alpha$较小时梯度下降的速度会很慢，训练时间更长，当$\alpha$较大时具有较快的学习速度，但是过大时会跳过代价函数的最低点，导致永远无法获得代价函数的最小值。因此，只要我们给定${\theta }_0,{\theta }_1$的初始值，让后进行逐步迭代，计算出每一步的偏导数项，最终就会走到$J({\theta }_0,{\theta }_1)$的低点，此时的${\theta }_0,{\theta }_1$就是模型的最优参数。

3 多元线性回归

  例如，房价可能与很多因素有关，如房屋面积、楼层、地段、房屋类型、房间数量等等。这样预测的模型可表示为$h_{\theta }(x_1,x_2,...,x_n)={\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$，${\theta }_0,{\theta }_1,...,{\theta }_n$被称为模型参数。总的来说多元线性回归跟一元线性回归基本相同。
$h_{\theta }(x_1,x_2,...,x_n)$矩阵形式：$$h_{\theta }(X)={\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n=(x_0,x_1,x_2,...,x_n)({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n{)}^T=X{\Theta }^T$$$$J(\theta )=\frac{1}{2}(h_{\theta }(X)-Y{)}^T(h_{\theta }(X)-Y)=\frac{1}{2}(X\theta -Y{)}^T(X\theta -Y)$$

  其中$x_0=1，$$Y$是样本的输出向量，维度为$m\times 1$， $1/2$在这主要是为了求导后系数为1，方便计算。

3.1 最小二乘法

  根据最小二乘法的原理，我们要对这个损失函数对$\theta$向量求导取0。结果如下式：
$$\frac{\partial }{\partial \theta }J(\theta )=X^T(X\theta -Y)=0$$
  这里面用到了矩阵求导链式法则，和两个个矩阵求导的公式。
  公式1：$\frac{\partial }{\partial X}(X^{T}X)=2X$，$X$为向量
  公式2：${\nabla }_{X}f(AX+B)=A^T{\nabla }_{Y}f，Y=AX+B，f(Y)$为标量
  对上述求导等式整理后可得：
$$X^T(X\theta -Y)=0$$$$\Rightarrow X^{T}X\theta =X^{T}Y$$$$\Rightarrow (X^{T}X{)}^{-1}(X^{T}X\theta )=(X^{T}X{)}^{-1}{X}^{T}Y$$$$\Rightarrow \theta =(X^{T}X{)}^{-1}{X}^{T}Y$$
  这里我们假设$(X^{T}X{)}^{-1}$是存在的，这样我们就一下子求出了模型参数$\theta$了，免去了代数法一个个去求导的麻烦。只要给了数据，我们就可以用$\theta =(X^{T}X{)}^{-1}{X}^{T}Y$算出$\theta$。

3.2 梯度下降

  与一元线性回归类似，初始化所有$\theta$，再求出偏导数逐步迭代，最终得到最小代价函数时$\theta$的值。
$\frac{\partial }{\partial \theta }J(\theta )=X^T(X\theta -Y)$
$\theta :=\theta -\alpha \frac{\partial }{\partial \theta }J(\theta )=\alpha X^T(X\theta -Y)$

4 多项式回归

  假定现在只考虑房价和房屋面积的关系，或许他们之间存在着多项式的关系，例如：
$$f(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_4{x}^4+...$$
  这就是多项式回归基本模型，其中${\theta }_0,{\theta }_1,{\theta }_2,...$均为模型参数。其求解方式与多元线性回归类似，因为我们可以作如下对应关系：$x_1=x,x_2=x^2,x_3=x^3,x_4=x^4,...$这样$f(x)$可表示为：
$$f(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_4{x}_4+...$$
  可以看出，与多元线性回归完全相似，其计算方法依然可以用多元线性回归的方法。

5 总结

  主要介绍了一元线性回归、多元线性回归、多项式回归的算法原理，解释了使用最小二乘法和梯度下降进行回归任务。下面对最小二乘法和梯度下降进行比较：

梯度下降	最小二乘
需要学习率$\alpha$	不需要
需要多次迭代	一次运算即可
当特征数量n较多时也好用	随着特征数量n的增多，运算付出的代价更大，中间需要计算矩阵的逆$(X^{T}X{)}^{-1}$，在n<10000时还可以接受
适用于各种类型的模型	只适用于线性模型

参考内容：https://blog.csdn.net/pxhdky/article/details/82388964