机器学习(聚类二)——K-Means
K-means算法,也称为K-平均或者K-均值,是一种使用广泛的最基础的聚类算法,一般作为掌握聚类算法的第一个算法。
思路
通过名字,大概就猜出这个算法的意思:K表示要分成K个类,而分类的手段是通过均值实现的。
假设输入样本为 T = X 1 , X 2 , . . . , X m T=X_1 ,X_2 ,...,X_m T=X1,X2,...,Xm ;则算法步骤为(使用欧几里得距离公式):
- 选择初始化的k个类别中心 a 1 , a 2 , . . . a k a_1 ,a_2 ,...a_k a1,a2,...ak ;
- 对于每个样本 X i X_i Xi ,将其标记为距离类别中心 a j a_j aj 最近的类别 j
- 更新每个类别的中心点 a j a_j aj 为隶属该类别的所有样本的均值
- 重复上面两步操作,直到达到某个中止条件
中止条件:
- 迭代次数、最小平方误差MSE、簇中心点变化率
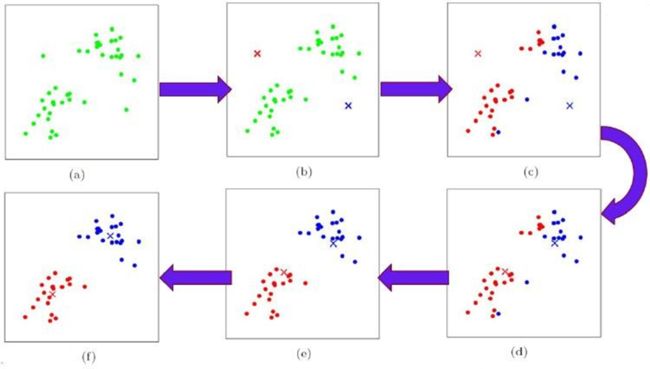
图中,找了两个起始点(图b),也就是初始质点。
计算其他所有点到这两个点的距离,离哪个点近就划分到这个点(图c)。
此时得到了两个簇,计算出每个簇的中心点,更新为新的质点(图d)。
以这两个点为基准再重新划分,得到两个新的簇(图c)。
……
不断迭代,直到满足我们的终止条件。
算法
记K个簇中心分别为 a 1 , a 2 , . . . a k a_1 ,a_2 ,...a_k a1,a2,...ak ;每个簇的样本数量为 N 1 , N 2 , . . . , N K N_1 ,N_2 ,...,N_K N1,N2,...,NK ;使用平方误差作为目标函数(使用欧几里得距离),公式为:
J ( a 1 , a 2 , … , a k ) = 1 2 ∑ j = 1 K ∑ i = 1 N j ( x i − a j ) 2 J(a_1,a_2,…,a_k )=\frac{1}{2} \sum_{j=1}^K\sum_{i=1}^{N_j}(x_i−a_j )^2 J(a1,a2,…,ak)=21j=1∑Ki=1∑Nj(xi−aj)2
上式为平方的形式,是关于未知参数是 a j a_j aj 一个凸函数,因此可通过求导的方式求最值。
要获取最优解,也就是目标函数需要尽可能的小,对 J J J 函数求偏导数,可以得到簇中心点a更新的公式为:
∂ J ∂ a j = ∑ i = 1 N j ( x i − a j ) 令 导 数 为 0 → a j = 1 N ∑ i = 1 N j x i \frac{∂J}{∂a_j}=\sum_{i=1}^{N_j}(x_i−a_j ) \quad \underrightarrow{\,令导数为0\,} \quad a_j= \frac{1}{N} \sum_{i=1}^{N_j}x_i ∂aj∂J=i=1∑Nj(xi−aj)令导数为0aj=N1i=1∑Njxi
这里思考一个问题:如果使用其它距离度量公式,簇中心点更新公式是啥?
思考
1 . K-means算法在迭代的过程中使用所有点的均值作为新的质点(中心点),如果簇中存在异常点,将导致均值偏差比较严重。
比如一个簇中有2、4、6、8、100五个数据,那么新的质点为24,显然这个质点离绝大多数点都比较远;
在当前情况下,使用中位数6可能比使用均值的想法更好,使用中位数的聚类方式叫做 K-Mediods聚类(K中值聚类)
2 . K-means算法是初值敏感的,选择不同的初始值可能导致不同的簇划分规则。
为了避免这种敏感性导致的最终结果异常性,可以采用初始化多套初始节点构造不同的分类规则,然后选择最优的构造规则。
如,我们预想的情况

而实际可能的情况(红点表示初始的质点)
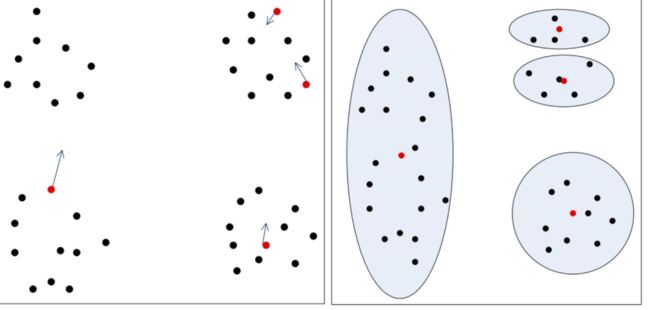
3 . 除此之外,初始值的数量选择不同,会得到不同的结果。
优缺点
1 .缺点:
- K值是用户给定的,在进行数据处理前,K值是未知的,不同的K值得到的结果也不一样;
- 对初始簇中心点是敏感的
- 不适合发现非凸形状的簇或者大小差别较大的簇,如同心圆
- 特殊值(离群值)对模型的影响比较大,可用K中值聚类
2 . 优点:
- 理解容易,聚类效果不错
- 处理大数据集的时候,该算法可以保证较好的伸缩性和高效率
- 当簇近似高斯分布的时候,效果非常不错,即上图这种成团的情况