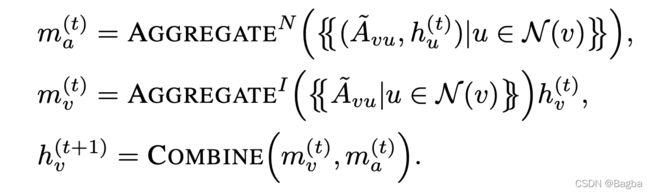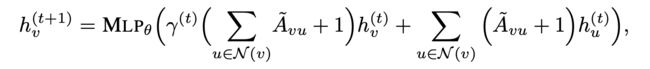ICLR2022 GNN 论文阅读笔记（一）GraphSNN

• 欢迎关注WX公众号，每周发布论文解析：PaperShare,
  点我关注

标题

A NEW PERSPECTIVE ON “HOW GRAPH NEURAL NET- WORKS GO BEYOND WEISFEILER-LEHMAN?”
（括号内的内容是个人见解，难免偏颇，望请指正）

---

主题

1. 理论上刻画了Message-Passing GNN 比WL-test 的表达能力更强。（当然，这是基于判断不同graph结构的测试上的结论，GNN还有另外一个表达能力就是学习节点等特征的能力。）
2. 基于以上理论，提出了GraphSNN，在多个区分图结构的数据集上取得了SOTA。

框架

定义：local isomorphism on neighborhood sub-graphs.

即在neighborhood sub-graphs 上的同构，就叫做邻居子图局部同构。（暂且这么翻译吧。。）

那么什么是neighborhood sub-graphs（邻居子图）呢？见上图：$G_1$中$v$的邻居子图$S_v$就是中间的$\{v_1...v_4\}$，包括$v$自己。

那么什么是overlap子图，比如，假设节点$v_1$的邻居子图为$S_{v1}$，那么，$S_{v1}$和$S_v$重叠的部分，即绿色椭圆部分，定义为$S_{v{v}_1}=S_v\cap S_{v_1}$，即含了$\{v1,v2,v\}$。再加上$S_{v{v}_2},S_{v{v}_3},S_{v{v}_4}$，即为over-subgraphs。

同理，可得出$G_2$的overlab subgraphs。

(Ok，再回到上面的图。上图中，首先分别计算出$G1,G2$中的节点$v,u$的overlap子图，然后用GMP(graph message passing)框架学习出两个节点的embedding：$h_v,h_u$，完事儿。)

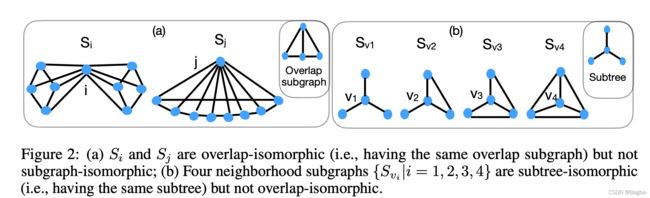
接下来作者定义了对于任意两个邻居子图$S_i,S_j$的三种同构类型：

1. subgraph-isomorphism: $S_i{\simeq }_{subgraph}{S}_j$

邻居子图是同构的；$v_1,v_2\in S_i$是相邻的，有且仅有当$g(v_1),g(v_2)\in S_j$也是相邻的，并且$h_{v_1}=h_{g(v_1)}$, $h_{v_2}=h_{g(v_2)}$

关于同构的定义其实很简单（即，对于任意两个图$G_1,G_2$, 存在一个bijective mapping，$g:G_1\to G_2$, 使得$g(i)=j$, $i\in Vertex(G_1),j\in Vertex(G_2)$，详见：等下补充下同构，WL-test相关知识）。

2. overlap-isomorphism: $S_i{\simeq }_{overlap}{S}_j$

即对于overlap子图中的每一个对overlap子图是subgraph-isomorphism的，即，$S_{iv}{\simeq }_{subgraph}{S}_{ju}$.

3. subtree-isomorphism: $S_i{\simeq }_{subtree}{S}_j$

只要求节点$i,j$到其邻居节点构成的图同构，并且$h_v=h_u$，$v\in \hat{N}(i)$, $u\in \hat{N}(j)$.

见图：

定理

定理一：${\simeq }_{subgraph}$ => ${\simeq }_{overlap}$ => ${\simeq }_{subtree}$,反过来不行，=>代表推出。

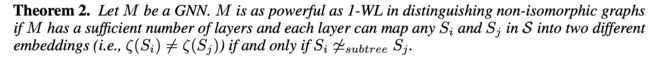
定理二：如果一个GNN 有足够多层，并且可以将$S_i,S_j$映射为不同的embeddings的时候，则GNN和WL-1 相当，有且仅当 $S_i/{\simeq }_{subtree}{S}_j$。

定理三：当一个GNN的agg策略满足下面这三个性质的，且有足够多层，并满足1）substree同构，subgraph不同构，$i$的邻居的multiset不等于$j$邻居的multiset。2）聚合函数$\Phi$是单射的；那么，该GNN就是严格的比1-WL要更具表达能力。(其实这个定义和[1] 中的WL kernel 用于subtree pattern的定义基本很像了。)

注：这里的kernel function:$w$即用来构造邻接矩阵$A$，比如$A_{vu}=w(S_v,S_{vu})$，而$A$就是决定了聚合的策略，即决定了邻居的权重。

模型

那么基于上面的理论，我们只要构造满足定理三的聚合函数$\Phi$的GNN就可以了。

这里$\gamma$是一个可学习的参数。

实验

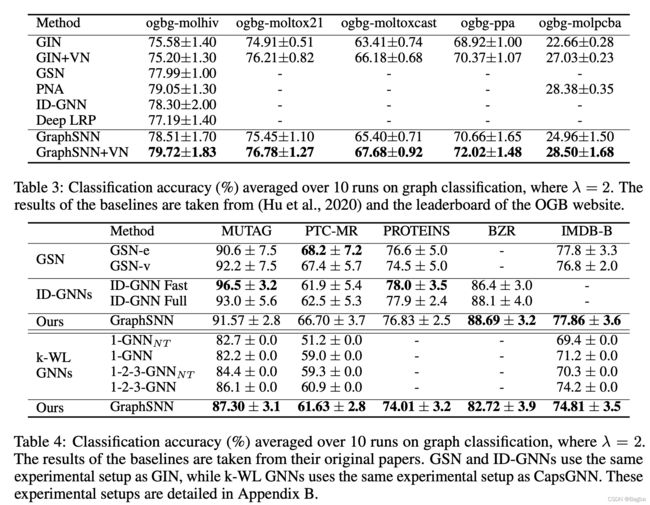
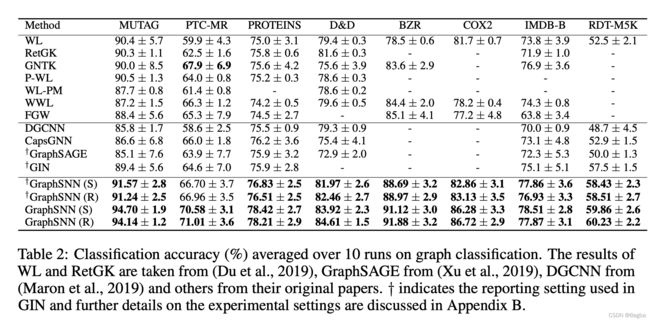
作者做了两类实验，一类是图节点分类，另外一类是图整体分类问题。效果都很好，图分类用到了Standford的OGB，我也在跑这个benchmark。但是没有对比最新SOTA（去年7月的），比如ppa，sota已经80+了，作者是72.

总结

（亮点主要是提出了一个新的视角来分析GNN表达能力。）

分析

（个人认为本文思路很像是[1]中继承而来，但是扩展了三种isomorphism，并且计算$w$的方式也比较有新意，可以从如何构造kernel function上面去挖掘新的想法。但是如果对于是没有 ground truth topology的任务，估计效果就不会很好，比如一些link prediction的任务。）

references

[1] Shervashidze, Nino, et al. “Weisfeiler-lehman graph kernels.” Journal of Machine Learning Research 12.9 (2011).