【R语言】白葡萄酒的EDA分析

1.项目相关信息

1.1 评估标准

1.2 项目模板

1.3 数据集列表

1.4 项目示例

大西洋飓风气象学
美国音乐家地理学
克里斯·萨登的《钻石探险》

1.5 数据选择

1.5.1 选择

白葡萄酒质量数据

1.5.2 详细数据说明

1.5.3 有关项目提交的常见问题

· 数据处理或转换（创建分类变量）应包含在 RMD 文件和最终拼合的 HTML 输出中。
· 未包含反思部分。
· 反思部分不是 RMD 文件中的最后一个部分。
· 未包含最终图形部分。
· 最终图形部分未处于 RMD 文件的结尾（在反思部分之前）。
· 最终图形部分未包含三个图形。
· 最终图形部分中的一个或多个图形未揭示出数据集的结果或模式。
· 最终图形未经修饰，并且缺失标题或单位。
· 为最终图形部分中的数据选择了不合适的图形。

2.环境准备

2.1 导入相关包

2.2 加载数据集

2 数据整理

2.1 数据评估

2.1.1 质量类问题

无

2.1.2 结构性问题

无

2.1 数据清洗

2.1.1 质量类问题整理

无

2.1.2 结构性问题整理

无

3.数据探索

3.1 数据概要认识

3.1.1 数据集介绍

##  [1] "rows=4898"
##  [1] "X"                    "fixed.acidity"        "volatile.acidity"    
##  [4] "citric.acid"          "residual.sugar"       "chlorides"           
##  [7] "free.sulfur.dioxide"  "total.sulfur.dioxide" "density"             
## [10] "pH"                   "sulphates"            "alcohol"             
## [13] "quality"
## [1] 6 5 7 8 4 3 9

数据集包含4898种⽩葡萄酒，及11个量化每种酒化学成分的变量。
⾄少3名葡萄酒专家对每种酒的质量进⾏了评分，分数在 0（⾮常差）和 10（⾮常好）之间。

nrow(wineQualityWhites)  
names(wineQualityWhites)  
unique(wineQualityWhites$quality)

3.1.2 数据字段概要描述

· fixed.acidity(g/l)：非挥发性酸度, 该变量指的是葡萄酒中的固定或者非挥发性酸度
· volatile.acidity(g/l)：挥发性酸度，葡萄酒中的醋酸含量过高，会导致醋的味道不愉快
· citric.acid(g/l)：柠檬酸，柠檬酸含量小，能给葡萄酒增添新鲜感和风味
· residual.sugar(g/l)：剩余糖分，发酵结束后剩下的糖分，很少发现低于1克/升的葡萄酒，超过45克/升的葡萄酒被认为是甜的
· chlorides(g/l)：酒中的盐量
· free.sulfur.dioxide(mg/l)：游离二氧化硫, 酒中带硫元素的离子，它可以防止微生物的生长和葡萄酒的氧化
· total.sulfur.dioxide(mg/l): 总二氧化硫，低浓度时检测不到，当浓度超过50 ppm时用鼻子可以闻到
· density(g/ml)：密度，大致接近于水，具体取决于酒精和糖的含量
· pH：用于描述酒的酸碱度
· sulphates(g/l)：硫酸盐，葡萄酒的添加剂，用于控制二氧化硫比例
· alcohol(% by volume)：酒中的酒精浓度
· quality：酒的质量，从0到10分不等

3.1.3 数据字段类型

## 'data.frame':    4898 obs. of  13 variables:
##  $ X                   : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ fixed.acidity       : num  7 6.3 8.1 7.2 7.2 8.1 6.2 7 6.3 8.1 ...
##  $ volatile.acidity    : num  0.27 0.3 0.28 0.23 0.23 0.28 0.32 0.27 0.3 0.22 ...
##  $ citric.acid         : num  0.36 0.34 0.4 0.32 0.32 0.4 0.16 0.36 0.34 0.43 ...
##  $ residual.sugar      : num  20.7 1.6 6.9 8.5 8.5 6.9 7 20.7 1.6 1.5 ...
##  $ chlorides           : num  0.045 0.049 0.05 0.058 0.058 0.05 0.045 0.045 0.049 0.044 ...
##  $ free.sulfur.dioxide : num  45 14 30 47 47 30 30 45 14 28 ...
##  $ total.sulfur.dioxide: num  170 132 97 186 186 97 136 170 132 129 ...
##  $ density             : num  1.001 0.994 0.995 0.996 0.996 ...
##  $ pH                  : num  3 3.3 3.26 3.19 3.19 3.26 3.18 3 3.3 3.22 ...
##  $ sulphates           : num  0.45 0.49 0.44 0.4 0.4 0.44 0.47 0.45 0.49 0.45 ...
##  $ alcohol             : num  8.8 9.5 10.1 9.9 9.9 10.1 9.6 8.8 9.5 11 ...
##  $ quality             : int  6 6 6 6 6 6 6 6 6 6 ...

总计13个(包括index)字段:
11个num类型字段: fixed.acidity, volatile.acidity, citric.acid, residual.sugar, chlorides, free.sulfur.dioxide, total.sulfur.dioxide, density, pH, sulphates, alcohol
2个int类型字段: index, quality

str(wineQualityWhites)

3.1.4 数据整理

## [1] 6 5 7 8 4 3 9

quality评分是一个在3~9之间取值离散变量，应该转换为factor类型。
另外，’X’变量是索引，在分析中没有任何意义，提前删除。

unique(wineQualityWhites$quality)
#将原有评分复制为quality_score
wineQualityWhites$quality_score = wineQualityWhites$quality
#将quality转换为factor类型
wineQualityWhites$quality = factor(wineQualityWhites$quality)
#去除在分析中不用的索引字段
wineQualityWhites = subset(wineQualityWhites, select = -c(X))

3.2 单变量分析

3.2.1 fixed.acidity：非挥发性酸度

3.2.1.1 histogram分布

ggplot(data = wineQualityWhites, aes(x=fixed.acidity))+  
       geom_histogram(binwidth = 0.2)+  
       scale_x_continuous(limits = c(0, 15), breaks = seq(0, 15, 1))

变量fixed.acidity呈正态分布，集中分布在[4, 10]这个取值区间内

3.2.1.2 箱型图

p1 = ggplot(data=wineQualityWhites, aes(x="", y=fixed.acidity))+
     geom_boxplot()
p2 = ggplot(data=wineQualityWhites, aes(x="", y=fixed.acidity))+
     geom_boxplot()+
     coord_cartesian(ylim = c(6, 8))
grid.arrange(p1, p2, ncol=2)

从箱型图中，可以看出变量fixed.acidity超过90%的值分布在[6.0, 7.5]区间内

3.2.2 volatile.acidity：挥发性酸度

3.2.2.1 histogram分布

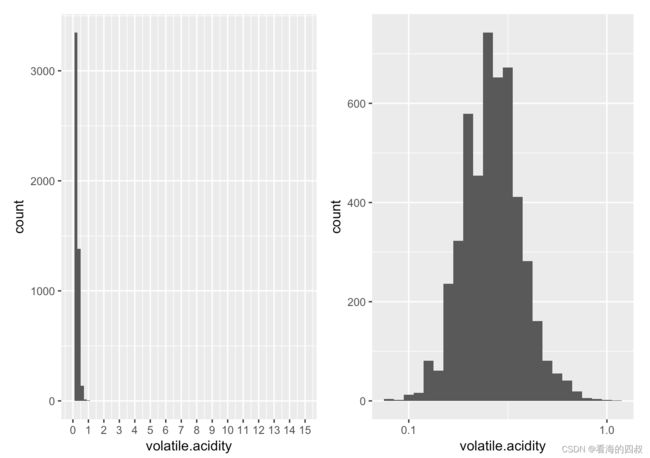
p1 = ggplot(data=wineQualityWhites, aes(x=volatile.acidity))+
     geom_histogram(binwidth = 0.2)+
     scale_x_continuous(limits = c(0, 15), breaks = seq(0, 15, 1))
p2 = ggplot(data=wineQualityWhites, aes(x=volatile.acidity))+
     geom_histogram(binwidth = 0.05)+
     scale_x_log10()
grid.arrange(p1, p2, ncol=2)

变量volatile.acidity呈长尾分布，通过log10转换后呈正太分布，主要集中分布在[0.1, 1]这个取值区间内

3.2.2.2 箱型图

p1 = ggplot(data=wineQualityWhites, aes(x="", y=volatile.acidity))+
  	 geom_boxplot()
p2 = ggplot(data=wineQualityWhites, aes(x="", y=volatile.acidity))+
 	 geom_boxplot()+
  	 coord_cartesian(ylim = c(0.2, 0.35))
grid.arrange(p1, p2, ncol=2)

从箱型图中，可以看出变量volatile.acidity超过90%的值分布在[0.2, 0.35]区间内

3.2.3 citric.acid：柠檬酸

3.2.3.1 histogram分布

ggplot(data=wineQualityWhites, aes(x=citric.acid))+
 	   geom_histogram(binwidth = 0.1)

可见大部分白葡萄酒的柠檬酸含量偏低，主要集中在[0,1.0]这个区间内。柠檬酸含量超过1.0的白葡萄酒极少

3.2.3.2 箱型图

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.0000  0.2700  0.3200  0.3342  0.3900  1.6600

summary(wineQualityWhites$citric.acid)
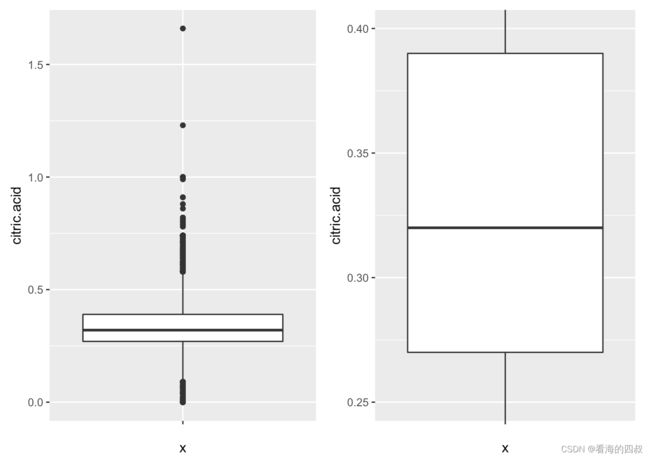
p1 = ggplot(data=wineQualityWhites, aes(x="", y=citric.acid))+
 			geom_boxplot()
p2 = ggplot(data=wineQualityWhites, aes(x="", y=citric.acid))+
  			geom_boxplot()+
  			coord_cartesian(ylim = c(0.25, 0.4))
grid.arrange(p1, p2, ncol=2)

变量citric.acid均值为0.3342，从箱型图可以看出，超过90%的值分布在[0.25, 0.4]区间内

3.2.4 residual.sugar：剩余糖分

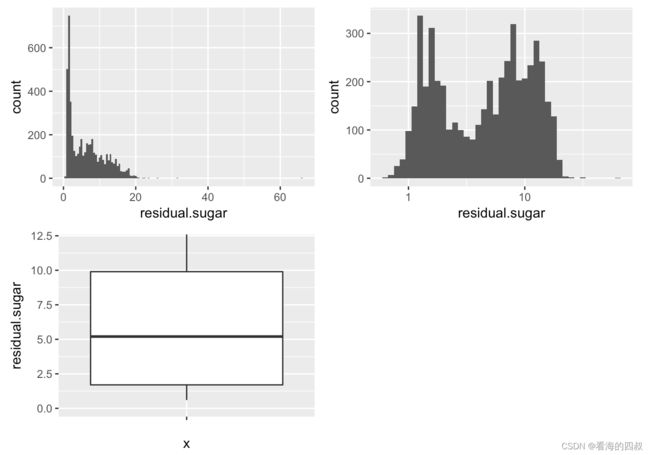
summary(wineQualityWhites$residual.sugar)
p1 = ggplot(data=wineQualityWhites, aes(x=residual.sugar))+
		    geom_histogram(binwidth = 0.5)
p2 = ggplot(data=wineQualityWhites, aes(x=residual.sugar))+
  			geom_histogram(binwidth = 0.05)+
  			scale_x_log10()
p3 = ggplot(data=wineQualityWhites, aes(x="", y=residual.sugar))+
  			geom_boxplot()+
  			coord_cartesian(ylim=c(0, 12))
grid.arrange(p1, p2, p3, ncol=2)

可见大部分白葡萄酒的剩余糖分偏低，超过90%集中在[0,12]这个区间，剩余糖分含量超过20的白葡萄酒极少。median值5.200小于mean值6.391也反映了这个事实。
另外通过log10转换后，residual.sugar分布呈双正态分布。也许是不同的人群对于两种级别甜度的白葡萄酒有偏好，因此葡萄酒生产商会偏向于生产这两种剩余糖分的白葡萄酒。

3.2.5 chlorides：含盐量

p1 = ggplot(data=wineQualityWhites, aes(x=chlorides))+
 			geom_histogram(binwidth = 0.005)+
  			scale_x_continuous(breaks = seq(0, 0.35, 0.02))
p2 = ggplot(data=wineQualityWhites, aes(x="", y=chlorides))+
  			geom_boxplot()+
  			coord_cartesian(ylim=c(0.03, 0.06))
grid.arrange(p1, p2, ncol=2)

大部分白葡萄酒的含盐量很低，绝对部分集中在[0.03,0.06]这个区间。酒基本不会有咸味，这与我们日常生活体验是相符的。

chlorides的分布似乎呈长尾分布，通过log10转换得到的分布更贴近正态分布。这可能是因为盐分含量本身低，而人们对盐度的感知基本要靠“数量级”层次的变化才能有明确的感知。因此在葡萄酒制造时，盐分相关的物质添加时也是按照这一规律来控制的。

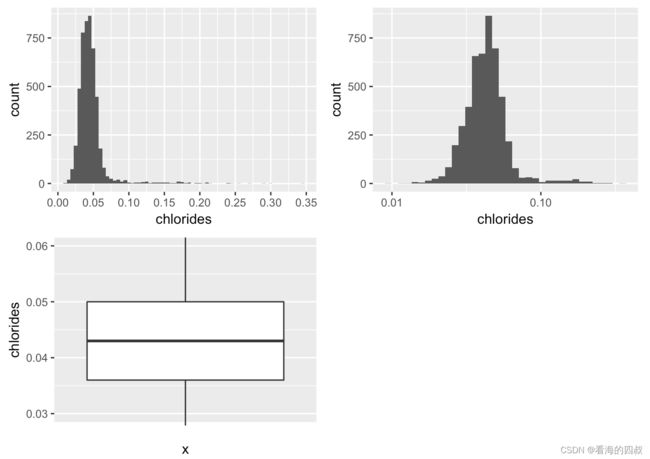
3.2.6 free.sulfur.dioxide：游离二氧化硫

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    2.00   23.00   34.00   35.31   46.00  289.00

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[-46.000000, [-11.500000, 80.500000], 115.000000]"

q = summary(wineQualityWhites$free.sulfur.dioxide)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = free.sulfur.dioxide))+
  			geom_histogram(binwidth = 10)+
  			scale_x_continuous(breaks = seq(0, 300, 20))
p2 = ggplot(data = wineQualityWhites, aes(x = "", y = free.sulfur.dioxide))+
 		    geom_boxplot()+
  			geom_hline(yintercept = 115.000000, col = "#FF6600")+
  			geom_hline(yintercept = 80.500000, col = "#6699FF")+
  			geom_hline(yintercept = -11.500000, col = "#6699FF")+
 			geom_hline(yintercept = -46.000000, col = "#FF6600")
grid.arrange(p1, p2, ncol = 2)

白葡萄酒的free.sulfur.dioxide超过95%集中在[0,80.500000]的区间内，基本符合正态分布。
wineQualityWhites数据的free.sulfur.dioxide存在极端异常值。这些异常值在后续模型和分析中需要处理。

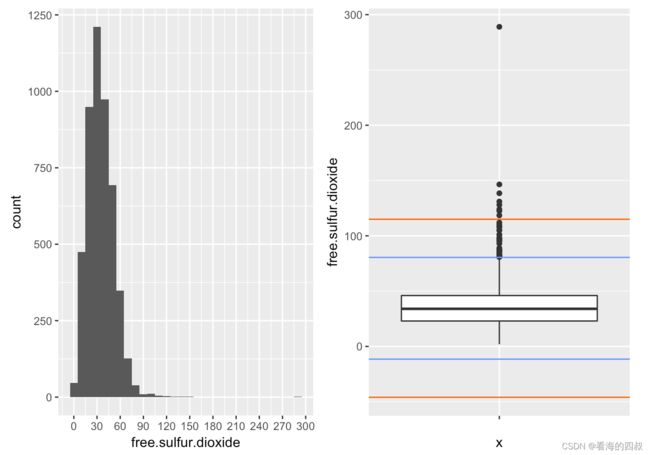
3.2.7 total.sulfur.dioxide：总二氧化硫

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##     9.0   108.0   134.0   138.4   167.0   440.0

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[-69.000000, [19.500000, 255.500000], 344.000000]"

q = summary(wineQualityWhites$total.sulfur.dioxide)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = total.sulfur.dioxide))+
  			geom_histogram(binwidth = 10)+
  			scale_x_continuous(breaks = seq(0, 450, 25))
p2 = ggplot(data = wineQualityWhites, aes(x = "", y = total.sulfur.dioxide))+
 			geom_boxplot()+
  			geom_hline(yintercept = 344.000000, col = "#FF6600")+
  			geom_hline(yintercept = 255.500000, col = "#6699FF")+
  			geom_hline(yintercept = 19.500000, col = "#6699FF")+
  			geom_hline(yintercept = -69.000000, col = "#FF6600")
grid.arrange(p1, p2, ncol = 2)

白葡萄酒的total.sulfur.dioxide超过95%集中在[19.5,255.500000]的区间内，基本呈正态分布。
wineQualityWhites数据的total.sulfur.dioxide存在少量极大异常值，超出了Q3+3IQR范围。这些异常值在后续模型和分析中需要处理。

3.2.8 density：密度

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.9871  0.9917  0.9937  0.9940  0.9961  1.0390

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[0.978590, [0.985156, 1.002666], 1.009232]"

q = summary(wineQualityWhites$density)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = density))+
  			geom_histogram(binwidth = 0.001)+
  			scale_x_continuous(breaks = seq(0, 1.04, 0.005))
p2 = ggplot(data = wineQualityWhites, aes(x = "", y = density))+
 			geom_boxplot()+
  			coord_cartesian(ylim = c(0.985, 1.005))
grid.arrange(p1, p2, ncol = 2)

大部分白葡萄酒的密度略低于水密度1，酒中包含酒精和一些矿物质、维生素等成分。其中酒精密度低于水，矿物质和维生素成分高于水，但可能由于酒精含量高于矿物质+维生素成分，所以拉低了葡萄酒密度。
另外通过boxplot可知，wineQualityWhites数据的density存在极端异常值。这些异常值在后续模型和分析中需要处理。

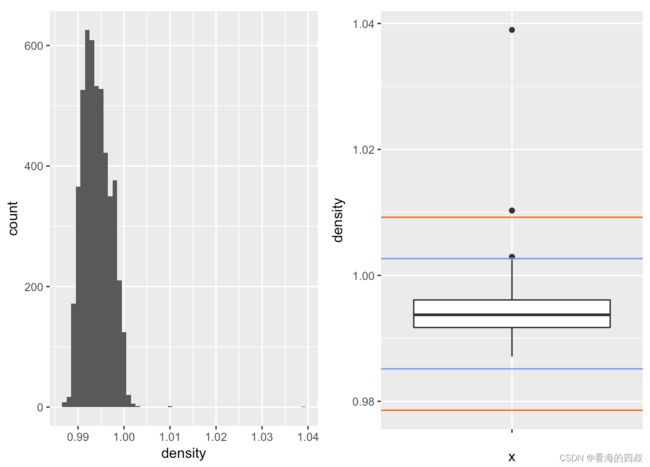
3.2.9 pH：酸碱度

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   2.720   3.090   3.180   3.188   3.280   3.820

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[2.520000, [2.805000, 3.565000], 3.850000]"

q = summary(wineQualityWhites$pH)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = pH))+
  			geom_histogram(binwidth = 0.02)+
  			scale_x_continuous(breaks = seq(2.7, 3.9, 0.1))
p2 = ggplot(data=wineQualityWhites, aes(x="", y=pH))+
  			geom_boxplot()+
  			geom_hline(yintercept = 3.850000, col = "#FF6600")+
  			geom_hline(yintercept = 3.565000, col = "#6699FF")+
  			geom_hline(yintercept = 2.805000, col = "#6699FF")+
  			geom_hline(yintercept = 2.520000, col = "#FF6600")
grid.arrange(p1, p2, ncol = 2)

根据数据的结构可知葡萄酒中含有酸性成分，因此它们的pH均低于7。并且葡萄酒基本呈酸味，因此可以猜测葡萄酒呈酸性，这也与“酸性物质pH低于7”的常识相符。
该变量包含了少数1.5倍IQR的异常值，但没有3倍IQR异常值。

3.2.10 sulphates：硫酸盐

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.2200  0.4100  0.4700  0.4898  0.5500  1.0800

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[-0.010000, [0.200000, 0.760000], 0.970000]"

q = summary(wineQualityWhites$sulphates)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = sulphates))+
  			geom_histogram(binwidth = 0.02)+
  			scale_x_continuous(breaks = seq(0.2, 1.1, 0.1))
p2 = ggplot(data = wineQualityWhites, aes(x = "", y = sulphates))+
  			geom_boxplot()+
  			geom_hline(yintercept = 0.97, col = "#FF6600")+
  			geom_hline(yintercept = 0.76, col = "#6699FF")+
  			geom_hline(yintercept = 0.2, col = "#6699FF")+
  			geom_hline(yintercept = -0.01, col = "#FF6600")
grid.arrange(p1, p2, ncol = 2)

白葡萄酒的sulphates超过95%集中在[0.20,0.76]的区间内，基本呈正态分布。
wineQualityWhites数据的sulphates存在较多超出Q3+1.5IQR的异常值，及少量的超出Q3+3IQR范围的极大异常值。这些异常值在后续模型和分析中需要处理。

3.2.11 alcohol：酒精浓度

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    8.00    9.50   10.40   10.51   11.40   14.20

## [1] "[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[3.800000, [6.650000, 14.250000], 17.100000]"

q = summary(wineQualityWhites$alcohol)
print(q)
sprintf("[Q1-3IQR, [Q1-1.5IQR, Q3+1.5IQR], Q3+3IQR]=[%f, [%f, %f], %f]",
        q['1st Qu.']-3*(q['3rd Qu.']-q['1st Qu.']), 
        q['1st Qu.']-1.5*(q['3rd Qu.']-q['1st Qu.']), 
        q['3rd Qu.']+1.5*(q['3rd Qu.']-q['1st Qu.']),
        q['3rd Qu.']+3*(q['3rd Qu.']-q['1st Qu.']))
p1 = ggplot(data = wineQualityWhites, aes(x = alcohol))+
  			geom_histogram(binwidth = 0.1)+
  			scale_x_continuous(breaks = seq(0, 15, 0.5))
p2 = ggplot(data = wineQualityWhites, aes(x = "", y = alcohol))+
  			geom_boxplot()+
  			geom_hline(yintercept = 17.100000, col = "#FF6600")+
  			geom_hline(yintercept = 14.250000, col = "#6699FF")+
  			geom_hline(yintercept = 6.650000, col = "#6699FF")+
  			geom_hline(yintercept = 3.800000, col = "#FF6600")
grid.arrange(p1, p2, ncol = 2)

白葡萄酒一般酒精浓度较低，从图中可以看出超过14°以上的白葡萄酒极为稀少，绝大部分白葡萄酒在8°~13°之间。这与葡萄酒一般没有烈酒的常识相符。
该变量基本没有异常值。

3.2.12 quality：质量评分

ggplot(data=wineQualityWhites, aes(x=quality))+
  	   geom_bar()

白葡萄酒quality评分一般是0~10分之间。但wineQualityWhites数据说明分数在[0, 3]和[9, 10]的白葡萄酒极为稀少。大多数白葡萄酒评分集中在[5, 7]内。酒评分基本符合正态分布。

3.2.13 反思

反思问题1

对于boxplot中的一些异常值，该如何处理。 是需要等到模型生成的时候进行删除？还是说少量的异常值可以忽略不计？

3.3 分析两个变量

3.3.1 酸度与pH值

3.3.1.1 pH与各种酸的关系

## [1] "relevance between fixed.acidity and pH is : -0.425858"
## [1] "relevance between volatile.acidity and pH is : -0.031915"
## [1] "relevance between citric.acid and pH is : -0.163748"

p1 = ggplot(data = wineQualityWhites, aes(x = fixed.acidity, y = pH))+
  			geom_point()+
  			geom_smooth(method = 'lm')
p2 = ggplot(data = wineQualityWhites, aes(x = volatile.acidity, y = pH))+
  			geom_point()+
  			geom_smooth(method = 'lm')
p3 = ggplot(data = wineQualityWhites, aes(x = citric.acid, y = pH))+
  			geom_point()+
  			geom_smooth(method = 'lm')
grid.arrange(p1, p2, p3, ncol = 1)

fixed.acidity.pH.rel = with(wineQualityWhites, cor.test(fixed.acidity, pH), method = c("pearson"))
volatile.acidity.pH.rel = with(wineQualityWhites, cor.test(volatile.acidity, pH), method = c("pearson"))
citric.acid.pH.rel = with(wineQualityWhites, cor.test(citric.acid, pH), method = c("pearson"))
sprintf("relevance between fixed.acidity and pH is : %f",fixed.acidity.pH.rel['estimate'])
sprintf("relevance between volatile.acidity and pH is : %f", volatile.acidity.pH.rel['estimate'])
sprintf("relevance between citric.acid and pH is : %f", citric.acid.pH.rel['estimate'])

从图中可以看出来pH值与volatile.acidity没有太大相关性。
可能因为是挥发性酸，因此水溶性不好，不容易生成H离子，因此对酸度影响不大。
而pH与fixed.acidity, citric.acid呈负相关性。即fixed.acidity,citric.acid含量高的白葡萄酒，其pH也高。
酸性物质含量高pH值越低，这与化学原理相符

通过相关性测试值
relevance between fixed.acidity and pH is : -0.425858
relevance between volatile.acidity and pH is : -0.031915
relevance between citric.acid and pH is : -0.163748
也可以得出相应结论。
并且fixed.acidity与pH相关性值为-0.42585，对于pH影响最大。

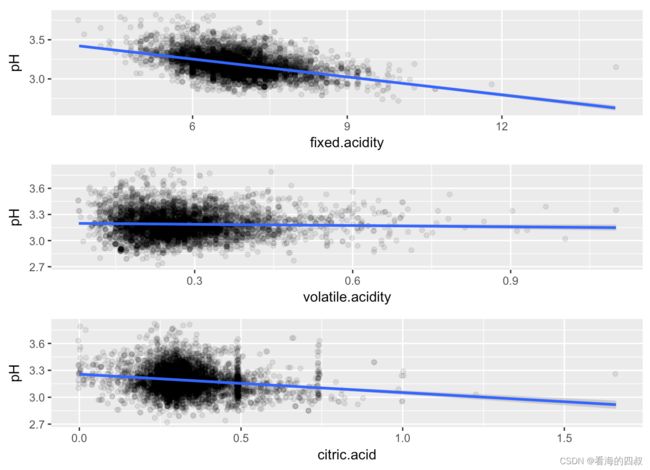
3.3.2 酸度与成分

3.3.2.2 citric.acid与fixed.acidity,volatile.acidity之间关系

## [1] "relevance between citric.acid and volatile.acidity is : -0.149472"
## [1] "relevance between citric.acid and fixed.acidity is : 0.289181"

稳定性酸与挥发性酸有没有可能是柠檬酸的不同成分而产生的？
这里通过柠檬酸与稳定性酸、挥发性酸的相关性来得出结论。

citric_and_volatile.acidity.rel = with(wineQualityWhites, 
                                     cor.test(citric.acid, volatile.acidity))
citric_and_fixed.acidity.rel = with(wineQualityWhites, 
                                  cor.test(citric.acid, fixed.acidity))
sprintf("relevance between citric.acid and volatile.acidity is : %f",
        citric_and_volatile.acidity.rel['estimate'])
sprintf("relevance between citric.acid and fixed.acidity is : %f",
        citric_and_fixed.acidity.rel['estimate'])

p1 = ggplot(data = wineQualityWhites, aes(x = citric.acid, y = volatile.acidity))+
  			geom_point()
p2 = ggplot(data = wineQualityWhites, aes(x = citric.acid, y = fixed.acidity))+
  			geom_point()
grid.arrange(p1, p2, ncol = 1)

从图和相关性测试值 relevance between citric.acid and volatile.acidity is : -0.149472
relevance between citric.acid and fixed.acidity is : 0.289181
可以看出citric.acid与volatile.acidity呈微弱的负相关性，与fixed.acidity呈正的弱相关性。
挥发性酸应该不是柠檬酸的成分。而柠檬酸应该是稳定性酸的一部分。

3.3.2.3 sulphates,free.sulfur.dioxide,total.sulfur.dioxide三者的关系

猜想1：由于sulphates是用于控制二氧化硫的，那么sulphates与total.sulfur.dioxide应该呈负相关性
猜想2：sulphates这一化学成分应该是free.sulfur.dioxide主要构成部分

## [1] "relevance between sulphates and total.sulfur.dioxide is : 0.134562"
## [1] "relevance between sulphates and free.sulfur.dioxide is : 0.059217"

total.sulfur_and_sulphates.rel = with(wineQualityWhites, 
                                    cor.test(sulphates, total.sulfur.dioxide))
free.sulfur_and_sulphates.rel = with(wineQualityWhites, 
                                   cor.test(sulphates, free.sulfur.dioxide))
sprintf("relevance between sulphates and total.sulfur.dioxide is : %f",
        total.sulfur_and_sulphates.rel['estimate'])
sprintf("relevance between sulphates and free.sulfur.dioxide is : %f",
        free.sulfur_and_sulphates.rel['estimate'])

p1 = ggplot(data = wineQualityWhites, aes(x = total.sulfur.dioxide, y = sulphates)) + geom_point()
p2 = ggplot(data = wineQualityWhites, aes(x = free.sulfur.dioxide, y = sulphates)) + geom_point()
grid.arrange(p1, p2, ncol = 1)

从图和相关性测试值 relevance between sulphates and total.sulfur.dioxide is : 0.134562
relevance between sulphates and free.sulfur.dioxide is : 0.059217
可以看出sulphates与total.sulfur.dioxide, free.sulfur.dioxide的相关性都很弱。
即sulphates硫酸盐添加剂对葡萄酒中的二氧化硫含量影响不大，对free.sulfur.dioxide游离硫离子的影响更是微乎其微。

3.3.3 白葡萄酒密度density

3.3.3.1 density与alcohol,sulphates,citric.acid,total.sulfur.dioxide的关系

疑问1：density会受到酒精含量、硫酸盐、二氧化硫、柠檬酸等成分的影响，但主要影响成分是哪些？
疑问2：是否因为酒精含量明显高于其它化学成分，才导致了density低于1

## [1] "relevance between density and alcohol is : -0.780138"
## [1] "relevance between density and sulphates is : 0.074493"
## [1] "relevance between density and citric.acid is : 0.149503"
## [1] "relevance between density and total.sulfur.dioxide is : 0.529881"
## [1] "relevance between density and residual.sugar is : 0.838966"

# 由于alcohol的密度是0.789/ml,并且wineQualityWhites中给出的单位是% by volume
# 因此对alcohol变量作了789*alcohol/100的转换，转成了g/l单位
p1 = ggplot(data = wineQualityWhites, aes(x = 789*alcohol/100, y = density))+
  			geom_point(alpha = 1/5, position = position_jitter(h = 0))+ xlab("alcohol(g/l)")
p2 = ggplot(data = wineQualityWhites, aes(x = sulphates, y = density))+
  			geom_point(alpha = 1/5, position = position_jitter(h = 0))+
  xlab("sulphates(g/l)")
p3 = ggplot(data = wineQualityWhites, aes(x = citric.acid, y = density))+
  			geom_point(alpha = 1/10, position = position_jitter(h = 0))+
  xlab("citric.acid(g/l)")
#wineQualityWhites中给出的单位是mg/dm^3，因此需要除以1000转换成单位(g/dm^3)
p4 = ggplot(data = wineQualityWhites, aes(x = total.sulfur.dioxide/1000, y = density))+ geom_point(alpha = 1/10, position = position_jitter(h = 0))+
  xlab("total.sulfur.dioxide(g/l)")
p5 = ggplot(data = wineQualityWhites, aes(x = residual.sugar, y = density))+
  geom_point(alpha = 1/10, position = position_jitter(h = 0))+
  xlab("residual.sugar(g/l)")
grid.arrange(p1, p2, p3, p4, p5, ncol = 2)

density.alcohol.rel = with(wineQualityWhites, cor.test(density, alcohol))
density.residual.sugar.rel = with(wineQualityWhites, cor.test(density, residual.sugar))
density.sulphates.rel = with(wineQualityWhites, cor.test(density, sulphates))
density.citric.acid.rel = with(wineQualityWhites, cor.test(density, citric.acid))
density.total.sulfur.dioxide.rel = with(wineQualityWhites, cor.test(density, total.sulfur.dioxide))
sprintf("relevance between density and alcohol is : %f", 
        density.alcohol.rel['estimate'])
sprintf("relevance between density and sulphates is : %f", 
        density.sulphates.rel['estimate'])
sprintf("relevance between density and citric.acid is : %f", 
        density.citric.acid.rel['estimate'])
sprintf("relevance between density and total.sulfur.dioxide is : %f",
        density.total.sulfur.dioxide.rel['estimate'])
sprintf("relevance between density and residual.sugar is : %f",
        density.residual.sugar.rel['estimate'])

把alcohol,sulphates,citric.acid,total.sulfur.dioxide,residual.sugar五种化学成分都转化成g/l单位，再绘制它们与density的scatter图。
其中alcohol, residual.sugar, 与density有较高相关性，total.sulfur.dioxide与密度有一定相关性，sulphates, citric.acid与density相关性几乎可以忽略。 从中容易看出含量高的成分对density影响大。

另外alcohol与密度呈负相关性，residual.sugar, total.sulfur.dioxide与density呈正相关性。 这个现象是因为alcohol密度低于水，因此含量越高，酒密度越低。
而residual.sugar, total.sulfur.dioxide密度高于水，因此含量越高酒密度越高。

3.3.4 质量评分

## [1] "relevance between quality and volatile.acidity is : -0.194723"
## [1] "relevance between quality and total.sulfur.dioxide is : -0.174737"
## [1] "relevance between quality and alcohol is : 0.435575"
## [1] "relevance between quality and citric.acid is : -0.009209"
## [1] "relevance between quality and chlorides is : -0.209934"
## [1] "relevance between quality and residual.sugar is : -0.097577"

人对酒的感知一般通过气味，口感这两个维度来感知。 而影响气味的主要包括volatile.acidity，alcohol，total.sulfur.dioxide，citric.acid这四个成分。影响口感则主要是citric.acid, chlorides，residual.sugar和alcohol。
疑问：酒的质量评分quality是否与volatile.acidity, total.sulfur.dioxide，citric.acid, chlorides, residual.sugar, alcohol存在什么关系呢？

p1 = ggplot(data = wineQualityWhites, aes(x = quality, y = volatile.acidity))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+ geom_smooth(method = 'lm', aes(group = 1))
p2 = ggplot(data = wineQualityWhites, aes(x = quality, y = total.sulfur.dioxide))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
  			geom_smooth(method = 'lm', aes(group = 1))
p3 = ggplot(data = wineQualityWhites, aes(x = quality, y = alcohol))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
  			geom_smooth(method = 'lm', aes(group = 1))
p4 = ggplot(data = wineQualityWhites, aes(x = quality, y = citric.acid))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
 	 		geom_smooth(method = 'lm', aes(group = 1))
p5 = ggplot(data = wineQualityWhites, aes(x = quality, y = chlorides))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
  			geom_smooth(method = 'lm', aes(group = 1))
p6 = ggplot(data = wineQualityWhites, aes(x = quality, y = residual.sugar))+
  			geom_jitter(alpha = 0.3) +
  			geom_boxplot(alpha = 0.3, color = 'blue')+
  			stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
  			geom_smooth(method = 'lm', aes(group = 1))
grid.arrange(p1, p2, p3, p4, p5, p6, ncol = 2)

quality.volatile.acidity.rel = with(wineQualityWhites, cor.test(quality_score, volatile.acidity))
quality.total.sulfur.dioxide.rel = with(wineQualityWhites, cor.test(quality_score, total.sulfur.dioxide))
quality.alcohol.rel = with(wineQualityWhites, cor.test(quality_score, alcohol))
quality.citric.acid.rel = with(wineQualityWhites, cor.test(quality_score, citric.acid))
quality.chlorides.rel = with(wineQualityWhites, cor.test(quality_score, chlorides))
quality.sugar.rel = with(wineQualityWhites, cor.test(quality_score, residual.sugar))

sprintf("relevance between quality and volatile.acidity is : %f",
        quality.volatile.acidity.rel['estimate'])
sprintf("relevance between quality and total.sulfur.dioxide is : %f", 
        quality.total.sulfur.dioxide.rel['estimate'])
sprintf("relevance between quality and alcohol is : %f", 
        quality.alcohol.rel['estimate'])
sprintf("relevance between quality and citric.acid is : %f", 
        quality.citric.acid.rel['estimate'])
sprintf("relevance between quality and chlorides is : %f", 
        quality.chlorides.rel['estimate'])
sprintf("relevance between quality and residual.sugar is : %f", 
        quality.sugar.rel['estimate'])

从图中可以看出quality与volatile.acidity,citric.acid,chlorides相关性微弱，只有与alcohol有一定相关性。 并且当quality在5分及以上时，这个特征体现的特别明显，即alcohol浓度越高quality分数也越高，呈明显的正相关性。

相关性测试，也能说明这一点。

relevance between quality and volatile.acidity is : -0.194723
relevance between quality and total.sulfur.dioxide is : -0.174737
relevance between quality and alcohol is : 0.435575
relevance between quality and citric.acid is : -0.009209
relevance between quality and chlorides is : -0.209934
relevance between quality and residual.sugar is : -0.097577

3.3.5 散点矩阵图分析

3.3.5.1 散点矩阵图观察

最后通过散点矩阵图看下还是否存在其它较强的变量间相关性。

theme_set(theme_minimal(20))
ggpairs(wineQualityWhites[sample.int(nrow(wineQualityWhites), 1000), ], 
        axisLabels = 'internal')+
        theme_gray()

ggcorr(wineQualityWhites, method = c("all.obs", 'spearman'),
       nbreaks = 4, palette = 'PuOr', label = TRUE,
       name = "spearman corr coeff.(rho)",
       hjust = 0.8, angle = -70, size = 3)+
  	   ggtitle("Pearson Correlation coefficient Matrix")+
	   theme_gray()

从图中可以看出之前分析的结论在图中均有较好的体现，散点矩阵图图左下角的散点图与两个变量关系分析中的分析是一致的。
除了之前分析的一些变量关系之外，从散点矩阵图的左下角散点图中能够发现free.sulfur.dioxide和total.sulfur.dioxide也存在一定的线性关系，这是之前的分析中没有发现的。
这也是散点矩阵图的意义，即帮助我们发现一些之前可能没有意识到的一些变量关系。

这一发现以及之前分析的几个变量的关系，通过散点矩阵图右上角的相关性数值也能够有体现出来。
提取变量相关性值大于0.5的双变量列举如下：

relevance between total.sulfur.dioxide and free.sulfur.dioxide is : 0.607
relevance between total.sulfur.dioxide and density is : 0.524
relevance between density and residual.sugar is : 0.825
relevance between density and alcohol is : -0.794

图Pearson Correlation coefficient Matrix更清晰地描述了各个变量之间的相关性，与散点矩阵图中的相关性数值四舍五入之后一致。

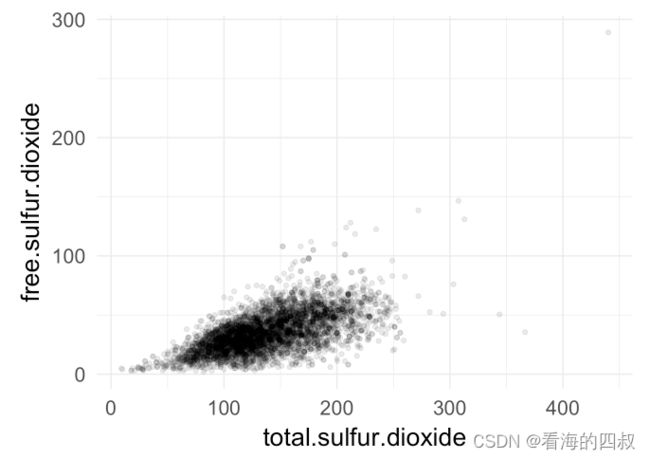
3.3.5.1 free.sulfur.dioxide与total.sulfur.dioxide的关系

最后看下free.sulfur.dioxide与total.sulfur.dioxide的关系。

## [1] "relevance between free.sulfur.dioxide and total.sulfur.dioxide is : 0.615501"

free.total.sulfur.rel = with(wineQualityWhites, cor.test(free.sulfur.dioxide, total.sulfur.dioxide))
sprintf("relevance between free.sulfur.dioxide and total.sulfur.dioxide is : %f",
        free.total.sulfur.rel['estimate'])

ggplot(data = wineQualityWhites, 
       aes(x = total.sulfur.dioxide, y = free.sulfur.dioxide))+
       geom_point()

首先
relevance between free.sulfur.dioxide and total.sulfur.dioxide is : 0.615501
可以知道free.sulfur.dioxide与total.sulfur.dioxide存在较强的相关性。
scatter图也较好地体现了这一相关性。
二氧化硫总含量越高，点解化到葡萄酒中的游离态的二氧化硫也越高，这是符合化学规律的。

3.3.6 反思

问题1：从两个变量的分析来看，没有找到与quality有特别明显关系的变量。
可能quality的影响因素角度，需要通过更多变量的组合关系来进行分析。
接下来会希望尝试多个变量组合来进行quality的分析和预测。

3.4 分析多个变量

在3.3两个变量分析的过程中，没有发现对质量评分quality起决定性因素的变量。
但从3.3.5中可知
relevance between total.sulfur.dioxide and free.sulfur.dioxide is : 0.607
relevance between total.sulfur.dioxide and density is : 0.524
relevance between density and residual.sugar is : 0.825
relevance between density and alcohol is : -0.794
接下来尝试通过组合更多的变量来探索与quality评分的关系。

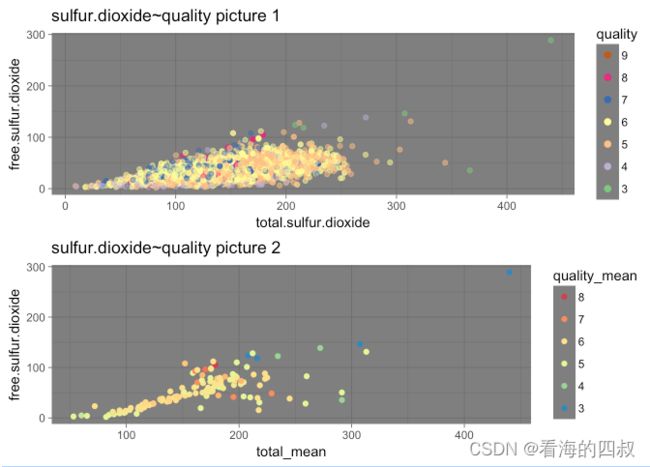
3.4.1 total.sulfur.dioxide+free.sulfur.dioxide对quality评分的影响

p1 = ggplot(data = wineQualityWhites, 
            aes(x = total.sulfur.dioxide, y = free.sulfur.dioxide,color = quality))+
  			geom_point( alpha = 0.3, size = 1, position = 'jitter')+
 			scale_color_brewer(type='Qual', palette='Accent',
    		guide = guide_legend(title = 'quality', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("sulfur.dioxide&quality picture 1")

sulfur.dioxide = wineQualityWhites %>% group_by(free.sulfur.dioxide) %>%
  				 summarise(total_mean = median(total.sulfur.dioxide),
            	 total_median = median(total.sulfur.dioxide),
            	 quality_mean = mean(quality_score)) %>% arrange(free.sulfur.dioxide)
p2 = ggplot(data = sulfur.dioxide, aes(x = total_mean, y = free.sulfur.dioxide, color = quality_mean))+
  			geom_point( alpha = 0.7, size = 2, position = 'jitter')+
  			scale_colour_distiller(type='div', palette='Spectral',
    		guide = guide_legend(title = 'quality_mean', reverse = T))+ 		
    		ggtitle("sulfur.dioxide&quality picture 2")
grid.arrange(p1, p2, ncol = 1)

从图sulfur.dioxide&quality pictures 1中可以高quality评分大体集中在total,free sulfur.dioxide不太高也不太低的中间区段。但这个区段内的quality评分分界不是太明显。
对free.sulfur.dioxide进行分组，计算quality和total.sulfur.dioxide的平均值。并描绘对应散点图，能够有更清晰的验证。

3.4.2 total.sulfur.dioxide+density对quality评分的影响

p1 = ggplot(data = wineQualityWhites, 
            aes(x = total.sulfur.dioxide, y = density,color = quality))+
  			geom_point(alpha = 0.1, size = 1, position = 'jitter')+
  			scale_color_brewer(type = 'Qual', palette = 'Accent',
    		guide = guide_legend(title = 'quality', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("picture 1")

density_sulfur.dioxide = wineQualityWhites %>% group_by(density) %>%
  						 summarise(total_mean = median(total.sulfur.dioxide),
            			 total_median = median(total.sulfur.dioxide),
            			 quality_mean = mean(quality_score)) %>% arrange(density)
p2 = ggplot(data = density_sulfur.dioxide, 
            aes(x = total_mean, y = density, color = quality_mean))+
  			geom_point( alpha = 0.5, size = 2, position = 'jitter')+
  			scale_colour_distiller(type = 'div', palette = 'Spectral',
    		guide = guide_legend(title = 'quality_mean', reverse = T))+
		    ggtitle("picture 2")
grid.arrange(p1, p2, ncol = 1)

从图picture 1中可以看出高quality评分[>=7]的散点集中在高density和低density两端，而低quality评分[<=6]的散点集中在density中段位置。
对density进行分组，计算quality和total.sulfur.dioxide的平均值。并描绘对应散点图picture 2，能够验证这一猜测。

3.4.3 density+residual.sugar对quality评分的影响

p1 = ggplot(data = wineQualityWhites, 
          	aes(x = residual.sugar,y = density,color = quality))+
  			coord_cartesian(xlim = c(0, 30))+
  			geom_point( alpha = 0.3, size = 1, position = 'jitter')+
  			scale_color_brewer(type='Qual', palette='Accent',
    		guide = guide_legend(title = 'quality', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("residual.sugar+density~quality picture 1")+
			theme_dark()

wineQualityWhites$quality_level = with(wineQualityWhites, 
                                     ifelse(quality_score>6, 'high', 'low'))
wineQualityWhites$quality_level = factor(wineQualityWhites$quality_level)
p2 = ggplot(data = wineQualityWhites, 
       		aes(x = residual.sugar, y = density,color = quality_level))+
  			geom_point( alpha = 0.3, size = 1, position = 'jitter')+
  			scale_color_brewer(type='Qual', palette='Paired',
    		guide = guide_legend(title = 'quality_level', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("residual.sugar+density~quality picture 2")+
  			theme_dark()+
  			coord_cartesian(xlim = c(0, 30))

p3 = ggplot(data = wineQualityWhites, aes(x = alcohol, y = density,color = quality))+
  			geom_point( alpha = 0.3, size = 1, position = 'jitter')+
 			scale_color_brewer(type='Qual', palette='Accent',
    		guide = guide_legend(title = 'quality', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("alcohol+density~quality picture")+
  			theme_dark()
grid.arrange(p1, p2, p3, ncol = 2)

从图residual.sugar+density~quality picture 1中可以看出高quality评分[>=7]的低quality评分[<=6]有较为明显的区分。
高quality评分[>=7]的散点集中在低desnity低residual.sugar和高density高residual.sugar区域。而低quality评分[<=6]则正好相反。
将高quality评分[>=7]和低quality评分[<=6]分成两种不同的颜色标识，得到图residual.sugar+density~quality picture 2。
可以清晰的看到高quality评分[>=7]和低quality评分[<=6]的白葡萄酒density与residual.sugar呈线性相关。并且高quality评分[>=7]的斜率明显高于低quality评分[<=6]的白葡萄酒。
这可能是因为高quality评分[>=7]的葡萄酒的acohol浓度较为集中，低quality评分[<=6]的alcohol浓度较为分散，见图alcohol+density~quality picture。而density的主要影响因素就是alcohol和residual.sugar。
因此高quality评分[>=7]白葡萄酒的residual.sugar含量对于density影响更明显，故具有更高的斜率，即residual.sugar含量增加一个单位，density提升的密度量也要更高一些。

3.4.4 density+alcohol对quality评分的影响

p1 = ggplot(data = wineQualityWhites, aes(x = alcohol, y = density,color = quality))+
  			geom_point(alpha = 0.6, size = 1, position = position_jitter(h = 0))+
  			scale_color_brewer(type = 'Qual', palette = 'Accent')+
  			ggtitle("alcohol+density~quality picture 1")+
  			theme_dark()

wineQualityWhites$quality_level = with(wineQualityWhites, 
                                     ifelse(quality_score>6, 'high', 'low'))
wineQualityWhites$quality_level = factor(wineQualityWhites$quality_level)
p2 = ggplot(data = wineQualityWhites, 
          	aes(x = alcohol, y = density,color = quality_level))+
  			geom_point(alpha = 0.5, size = 1, position = 'jitter')+
  			scale_color_brewer(type='Qual', palette='Accent',
    		guide = guide_legend(title = 'quality_level', reverse = T,
    		override.aes = list(alpha = 1, size = 2)))+
  			ggtitle("alcohol+density~quality picture 2")+
  			theme_dark()
grid.arrange(p1, p2, ncol = 1)

ggplot(data = wineQualityWhites, aes(x = alcohol, y = density,color = quality))+
   	   geom_point( alpha = 0.6, size = 1, position = 'jitter')+
  	   scale_color_brewer(type='Qual', palette='Accent',
       guide = guide_legend(title = 'quality', reverse = T,
       override.aes = list(alpha = 1, size = 2)))+
  	   facet_wrap(~quality)+
  	   ggtitle("alcohol+density~quality picture 3")+
  	   theme_grey()

从图alcohol+density~quality picture 1中可以看出高quality评分[>=7]的白葡萄酒大体分布在相对的低density高alcohol的区域以及少量的de高nsity低alcohol，而低quality评分[<=6]的散点集中在相对的高desnity低alcoho的区域。
将高quality评分[>=7]和低quality评分[<=6]分成两种不同的颜色标识，得到图alcohol+density~quality picture 2，有更明显的呈现。
这可能是因为density本身与alcohol呈负相关，而高quality评分[>=7]在alcohol的分布就更偏向于高浓度的alcohol，因此会出现这样的情况。
同时，从图alcohol+density~quality picture 3可以看出，alcohol与density不论在哪种quality评分下，都具有负向相关性，即酒精浓度越高，密度越低。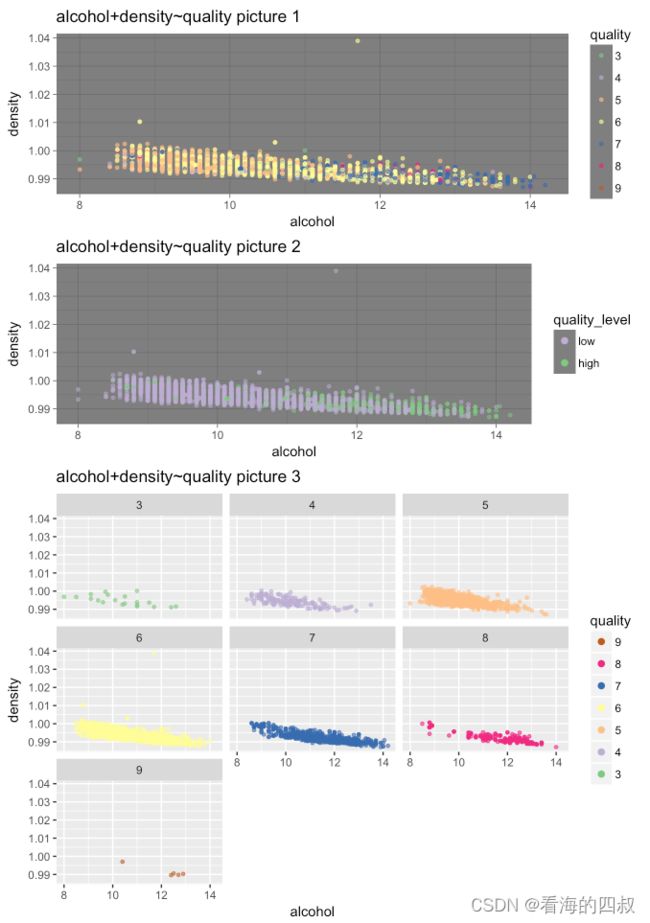

3.4.5 quality评分预测模型

从双变量和多变量都没有找到quality评分的决定性因素，仍然希望尝试通过机器学习算法对quality进行预测。
通过查看paperUsing Data Mining for Wine Quality Assessment可以知道，通过svm模型能够取得较好的quality预测效果。
因此接下来是对svm模型训练和预测检验。

## Call:
## svm(formula = quality_level ~ . - quality - quality_score, data = train[, 
##     -1])
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  1 
##       gamma:  0.1 
## 
## Number of Support Vectors:  3361
## 
##  ( 765 1016 1580 )
## 
## Number of Classes:  3 
## 
## Levels: 
##  bad good normal

##                 Length Class  Mode     
## call                3  -none- call     
## type                1  -none- character
## predicted        3918  factor numeric  
## err.rate         2000  -none- numeric  
## confusion          12  -none- numeric  
## votes           11754  matrix numeric  
## oob.times        3918  -none- numeric  
## classes             3  -none- character
## importance         10  -none- numeric  
## importanceSD        0  -none- NULL     
## localImportance     0  -none- NULL     
## proximity           0  -none- NULL     
## ntree               1  -none- numeric  
## mtry                1  -none- numeric  
## forest             14  -none- list     
## y                3918  factor numeric  
## test                0  -none- NULL     
## inbag               0  -none- NULL     
## terms               3  terms  call

## # weights:  703
## initial  value 4734.393371 
## iter  10 value 4076.043102
## iter  20 value 4032.743039
## iter  30 value 3975.438697
## iter  40 value 3861.607333
## iter  50 value 3819.895916
## iter  60 value 3691.288394
## iter  70 value 3629.001959
## iter  80 value 3552.538244
## iter  90 value 3444.420014
## iter 100 value 3411.465065
## final  value 3411.465065 
## stopped after 100 iterations

## a 10-50-3 network with 703 weights
## options were - softmax modelling  decay=0.001
##   b->h1  i1->h1  i2->h1  i3->h1  i4->h1  i5->h1  i6->h1  i7->h1  i8->h1 
##    0.68    1.18    0.15    1.92    0.78   -1.02    0.38    0.70    1.59 
##  i9->h1 i10->h1 
##   -0.30   -2.88 
##   b->h2  i1->h2  i2->h2  i3->h2  i4->h2  i5->h2  i6->h2  i7->h2  i8->h2 
##    0.05    0.91    0.01   -0.48   -0.65    0.15   -0.39    0.30    1.37 
##  i9->h2 i10->h2 
##    0.34    1.40 
##   b->h3  i1->h3  i2->h3  i3->h3  i4->h3  i5->h3  i6->h3  i7->h3  i8->h3 
##   -0.34    0.17    0.58    0.38   -0.09    1.17    0.69   -0.29   -0.34 
##  i9->h3 i10->h3 
##    0.50   -0.92 
##   b->h4  i1->h4  i2->h4  i3->h4  i4->h4  i5->h4  i6->h4  i7->h4  i8->h4 
##   -0.42   -0.58   -0.09   -0.21   -0.05   -0.31    0.52   -0.40   -0.81 
##  i9->h4 i10->h4 
##    0.17   -0.54 
##   b->h5  i1->h5  i2->h5  i3->h5  i4->h5  i5->h5  i6->h5  i7->h5  i8->h5 
##    0.26    0.13   -0.34   -0.19    0.43    1.08    1.13   -0.32    0.15 
##  i9->h5 i10->h5 
##    0.29    1.59 
##   b->h6  i1->h6  i2->h6  i3->h6  i4->h6  i5->h6  i6->h6  i7->h6  i8->h6 
##    0.27    0.25   -0.44   -0.64   -0.65    1.26    0.36   -0.03   -0.11 
##  i9->h6 i10->h6 
##    0.15   -1.29 
##   b->h7  i1->h7  i2->h7  i3->h7  i4->h7  i5->h7  i6->h7  i7->h7  i8->h7 
##   -0.32   -0.44   -0.67   -0.66    0.43   -0.17    0.50    0.63    0.38 
##  i9->h7 i10->h7 
##    0.27   -0.01 
##   b->h8  i1->h8  i2->h8  i3->h8  i4->h8  i5->h8  i6->h8  i7->h8  i8->h8 
##   -0.29   -0.03   -0.34   -0.82    0.26    0.47    0.45   -0.24    0.11 
##  i9->h8 i10->h8 
##   -0.44    0.25 
##   b->h9  i1->h9  i2->h9  i3->h9  i4->h9  i5->h9  i6->h9  i7->h9  i8->h9 
##    3.43    7.77    0.32   -0.09    1.31    0.03   -0.01    4.24    0.20 
##  i9->h9 i10->h9 
##   -2.40   -0.86 
##   b->h10  i1->h10  i2->h10  i3->h10  i4->h10  i5->h10  i6->h10  i7->h10 
##     0.05    -0.23     0.63    -0.55    -0.38    -1.19    -4.02    -0.09 
##  i8->h10  i9->h10 i10->h10 
##    -1.28     0.30    -4.04 
##   b->h11  i1->h11  i2->h11  i3->h11  i4->h11  i5->h11  i6->h11  i7->h11 
##     0.42    -0.09    -0.34    -0.54    -0.20     3.52    -1.98    -0.82 
##  i8->h11  i9->h11 i10->h11 
##    -1.10    -0.06    -1.58 
##   b->h12  i1->h12  i2->h12  i3->h12  i4->h12  i5->h12  i6->h12  i7->h12 
##     0.50     0.11     0.60     1.95    -0.17     1.11    -0.16    -0.01 
##  i8->h12  i9->h12 i10->h12 
##    -0.34     0.06    -2.99 
##   b->h13  i1->h13  i2->h13  i3->h13  i4->h13  i5->h13  i6->h13  i7->h13 
##     0.65     0.43    -0.58     0.52    -0.37     0.10     1.27     0.60 
##  i8->h13  i9->h13 i10->h13 
##    -0.48    -0.33    -0.02 
##   b->h14  i1->h14  i2->h14  i3->h14  i4->h14  i5->h14  i6->h14  i7->h14 
##     0.44    -0.02     0.32    -0.30     0.48    -0.55    -0.18    -0.16 
##  i8->h14  i9->h14 i10->h14 
##    -0.32    -0.37    -0.36 
##   b->h15  i1->h15  i2->h15  i3->h15  i4->h15  i5->h15  i6->h15  i7->h15 
##    -0.33    -0.34    -0.47    -0.82    -0.25    -0.16     0.03     0.59 
##  i8->h15  i9->h15 i10->h15 
##    -0.22    -0.22     0.32 
##   b->h16  i1->h16  i2->h16  i3->h16  i4->h16  i5->h16  i6->h16  i7->h16 
##     0.54    -0.66    -0.21     0.80    -0.03    -0.05     1.59    -0.58 
##  i8->h16  i9->h16 i10->h16 
##    -0.20     0.38     0.24 
##   b->h17  i1->h17  i2->h17  i3->h17  i4->h17  i5->h17  i6->h17  i7->h17 
##     0.00    -0.57    -0.55    -0.66    -0.09     0.04    -0.10    -0.64 
##  i8->h17  i9->h17 i10->h17 
##     0.43    -0.35    -0.67 
##   b->h18  i1->h18  i2->h18  i3->h18  i4->h18  i5->h18  i6->h18  i7->h18 
##     0.47    -0.20     0.27    -0.59    -0.22    -0.57    -0.69    -0.34 
##  i8->h18  i9->h18 i10->h18 
##    -0.20     0.64     0.53 
##   b->h19  i1->h19  i2->h19  i3->h19  i4->h19  i5->h19  i6->h19  i7->h19 
##     0.46     0.52    -0.08    -0.06    -0.62     0.67     0.27    -0.16 
##  i8->h19  i9->h19 i10->h19 
##     0.64    -0.64    -0.22 
##   b->h20  i1->h20  i2->h20  i3->h20  i4->h20  i5->h20  i6->h20  i7->h20 
##     2.58     2.82     0.58    -0.13    -0.14    -0.19    -0.05     2.99 
##  i8->h20  i9->h20 i10->h20 
##     2.92     0.22    -0.97 
##   b->h21  i1->h21  i2->h21  i3->h21  i4->h21  i5->h21  i6->h21  i7->h21 
##    -0.16    -0.34     0.20     1.06    -0.25     0.15    -0.35    -0.29 
##  i8->h21  i9->h21 i10->h21 
##     0.29    -0.29     3.92 
##   b->h22  i1->h22  i2->h22  i3->h22  i4->h22  i5->h22  i6->h22  i7->h22 
##     0.06     0.32    -0.37    -0.59    -0.14    -0.04    -0.74     0.30 
##  i8->h22  i9->h22 i10->h22 
##     0.09     0.43     0.53 
##   b->h23  i1->h23  i2->h23  i3->h23  i4->h23  i5->h23  i6->h23  i7->h23 
##    -0.46     0.60    -0.02     0.38    -0.01     0.13     0.15     0.22 
##  i8->h23  i9->h23 i10->h23 
##    -0.38    -0.67     0.44 
##   b->h24  i1->h24  i2->h24  i3->h24  i4->h24  i5->h24  i6->h24  i7->h24 
##    -0.04     0.27    -0.56     0.14     0.32    -0.11     0.28    -0.28 
##  i8->h24  i9->h24 i10->h24 
##    -0.07    -0.36     0.42 
##   b->h25  i1->h25  i2->h25  i3->h25  i4->h25  i5->h25  i6->h25  i7->h25 
##     0.51    -0.42    -0.36     0.15     0.37    -0.34    -0.94     0.57 
##  i8->h25  i9->h25 i10->h25 
##    -0.48     0.22     0.72 
##   b->h26  i1->h26  i2->h26  i3->h26  i4->h26  i5->h26  i6->h26  i7->h26 
##     0.18     0.19     0.23    -0.67     0.22     0.00    -0.37    -0.65 
##  i8->h26  i9->h26 i10->h26 
##    -0.22    -0.66     0.32 
##   b->h27  i1->h27  i2->h27  i3->h27  i4->h27  i5->h27  i6->h27  i7->h27 
##    -0.32     0.41    -0.35     0.53     0.56    -0.61    -0.39     0.41 
##  i8->h27  i9->h27 i10->h27 
##    -0.32     0.22    -0.32 
##   b->h28  i1->h28  i2->h28  i3->h28  i4->h28  i5->h28  i6->h28  i7->h28 
##    -0.59    -0.45     0.01     0.46     0.11     0.06    -0.39    -0.31 
##  i8->h28  i9->h28 i10->h28 
##    -0.27     0.11    -0.17 
##   b->h29  i1->h29  i2->h29  i3->h29  i4->h29  i5->h29  i6->h29  i7->h29 
##    -0.48    -0.41    -0.37    -0.07     0.29    -0.20    -0.16    -0.42 
##  i8->h29  i9->h29 i10->h29 
##    -0.31    -0.56    -0.38 
##   b->h30  i1->h30  i2->h30  i3->h30  i4->h30  i5->h30  i6->h30  i7->h30 
##    -0.27     0.64     0.47     0.67     0.30    -0.51     0.05     0.67 
##  i8->h30  i9->h30 i10->h30 
##    -0.70     0.52     0.14 
##   b->h31  i1->h31  i2->h31  i3->h31  i4->h31  i5->h31  i6->h31  i7->h31 
##     0.01     0.21    -0.44     0.84    -0.12    -1.34    -2.86    -0.09 
##  i8->h31  i9->h31 i10->h31 
##    -0.79    -0.33    -5.24 
##   b->h32  i1->h32  i2->h32  i3->h32  i4->h32  i5->h32  i6->h32  i7->h32 
##     0.26    -0.55     0.40    -1.24    -0.66     0.51    -1.06    -0.02 
##  i8->h32  i9->h32 i10->h32 
##    -0.26     0.57    -1.31 
##   b->h33  i1->h33  i2->h33  i3->h33  i4->h33  i5->h33  i6->h33  i7->h33 
##    -0.63    -0.11     0.52     0.10     0.50    -0.04     0.25    -0.11 
##  i8->h33  i9->h33 i10->h33 
##    -0.64     0.64     0.63 
##   b->h34  i1->h34  i2->h34  i3->h34  i4->h34  i5->h34  i6->h34  i7->h34 
##     0.16    -0.52     0.30    -0.53     0.36     0.31    -0.02    -0.38 
##  i8->h34  i9->h34 i10->h34 
##    -0.38     0.15     0.12 
##   b->h35  i1->h35  i2->h35  i3->h35  i4->h35  i5->h35  i6->h35  i7->h35 
##     0.10     0.02     0.63     0.59    -0.41     0.29    -0.68     0.25 
##  i8->h35  i9->h35 i10->h35 
##     0.51     0.24     0.08 
##   b->h36  i1->h36  i2->h36  i3->h36  i4->h36  i5->h36  i6->h36  i7->h36 
##     0.64     0.14     0.07    -0.33    -0.35    -0.54    -0.06    -0.41 
##  i8->h36  i9->h36 i10->h36 
##    -0.65     0.00    -0.44 
##   b->h37  i1->h37  i2->h37  i3->h37  i4->h37  i5->h37  i6->h37  i7->h37 
##    -0.46     0.64    -0.60    -0.11     0.35    -0.67    -0.20     0.27 
##  i8->h37  i9->h37 i10->h37 
##    -0.20    -0.09    -0.27 
##   b->h38  i1->h38  i2->h38  i3->h38  i4->h38  i5->h38  i6->h38  i7->h38 
##     0.31     0.31    -0.63     0.46     0.15    -0.63    -0.60     0.11 
##  i8->h38  i9->h38 i10->h38 
##     0.04    -0.03    -0.14 
##   b->h39  i1->h39  i2->h39  i3->h39  i4->h39  i5->h39  i6->h39  i7->h39 
##    -0.30    -0.35     0.03     0.11     0.56    -0.46    -0.35    -0.41 
##  i8->h39  i9->h39 i10->h39 
##     0.59    -0.27    -0.03 
##   b->h40  i1->h40  i2->h40  i3->h40  i4->h40  i5->h40  i6->h40  i7->h40 
##    -1.24    -0.47    -0.91    -1.68    -0.11     1.82     1.25    -0.65 
##  i8->h40  i9->h40 i10->h40 
##    -2.28    -0.17    -7.45 
##   b->h41  i1->h41  i2->h41  i3->h41  i4->h41  i5->h41  i6->h41  i7->h41 
##     0.13    -0.09     0.14    -0.44     0.07    -0.58    -0.64    -0.60 
##  i8->h41  i9->h41 i10->h41 
##     0.05    -0.18    -0.58 
##   b->h42  i1->h42  i2->h42  i3->h42  i4->h42  i5->h42  i6->h42  i7->h42 
##    -0.05     0.73     0.18    -0.70     0.65     1.17    -1.85     0.57 
##  i8->h42  i9->h42 i10->h42 
##     0.68     0.37     2.63 
##   b->h43  i1->h43  i2->h43  i3->h43  i4->h43  i5->h43  i6->h43  i7->h43 
##     4.30     1.90     1.52     2.28    -0.04     0.19     0.32     4.12 
##  i8->h43  i9->h43 i10->h43 
##     9.78     0.48   -11.27 
##   b->h44  i1->h44  i2->h44  i3->h44  i4->h44  i5->h44  i6->h44  i7->h44 
##    -0.17     0.59     0.43     0.60    -0.32    -0.61     0.66     0.37 
##  i8->h44  i9->h44 i10->h44 
##     0.48    -0.49    -0.02 
##   b->h45  i1->h45  i2->h45  i3->h45  i4->h45  i5->h45  i6->h45  i7->h45 
##     0.28    -0.27     0.44     0.05     0.15     0.68     0.16     0.16 
##  i8->h45  i9->h45 i10->h45 
##     0.36    -0.59     0.08 
##   b->h46  i1->h46  i2->h46  i3->h46  i4->h46  i5->h46  i6->h46  i7->h46 
##     0.48     0.66     0.60    -1.89     0.58     0.18     0.78    -0.23 
##  i8->h46  i9->h46 i10->h46 
##    -0.24    -0.44    -0.51 
##   b->h47  i1->h47  i2->h47  i3->h47  i4->h47  i5->h47  i6->h47  i7->h47 
##     0.35    -0.36    -0.24    -0.20    -0.59     0.03     0.65     0.08 
##  i8->h47  i9->h47 i10->h47 
##     0.59    -0.07    -0.04 
##   b->h48  i1->h48  i2->h48  i3->h48  i4->h48  i5->h48  i6->h48  i7->h48 
##     0.23     0.47    -0.46    -0.52     0.11    -0.44     0.46    -0.21 
##  i8->h48  i9->h48 i10->h48 
##     0.23     0.19     0.01 
##   b->h49  i1->h49  i2->h49  i3->h49  i4->h49  i5->h49  i6->h49  i7->h49 
##    -0.23     0.27     0.12    -0.51    -0.15     0.15     0.63     0.46 
##  i8->h49  i9->h49 i10->h49 
##     0.13    -0.59     0.09 
##   b->h50  i1->h50  i2->h50  i3->h50  i4->h50  i5->h50  i6->h50  i7->h50 
##     0.08     0.24    -0.21     0.04    -0.36     0.11     1.14    -0.14 
##  i8->h50  i9->h50 i10->h50 
##     0.53    -0.53    -0.53 
##   b->o1  h1->o1  h2->o1  h3->o1  h4->o1  h5->o1  h6->o1  h7->o1  h8->o1 
##    0.29    1.10   -1.56   -0.45   -0.56    0.37    0.06    0.01   -0.28 
##  h9->o1 h10->o1 h11->o1 h12->o1 h13->o1 h14->o1 h15->o1 h16->o1 h17->o1 
##    4.32    0.72    0.83    0.68    0.21   -0.33    0.29   -1.17    0.67 
## h18->o1 h19->o1 h20->o1 h21->o1 h22->o1 h23->o1 h24->o1 h25->o1 h26->o1 
##    0.67   -0.43    2.50   -1.06    1.87   -0.42    0.10    2.15    0.39 
## h27->o1 h28->o1 h29->o1 h30->o1 h31->o1 h32->o1 h33->o1 h34->o1 h35->o1 
##    0.50    0.08    0.00    0.72    0.62    0.49   -0.03    0.13    0.35 
## h36->o1 h37->o1 h38->o1 h39->o1 h40->o1 h41->o1 h42->o1 h43->o1 h44->o1 
##    0.53    0.19    0.21    0.35   -1.09   -0.19    1.92    0.38    0.10 
## h45->o1 h46->o1 h47->o1 h48->o1 h49->o1 h50->o1 
##   -0.09    0.96   -0.34   -0.16    0.39   -0.43 
##   b->o2  h1->o2  h2->o2  h3->o2  h4->o2  h5->o2  h6->o2  h7->o2  h8->o2 
##    0.01   -0.59    0.81    0.05   -0.10   -0.09    0.32    0.01   -0.24 
##  h9->o2 h10->o2 h11->o2 h12->o2 h13->o2 h14->o2 h15->o2 h16->o2 h17->o2 
##   -4.50   -0.45   -0.20    0.13    0.31   -0.39   -0.97   -0.20    0.60 
## h18->o2 h19->o2 h20->o2 h21->o2 h22->o2 h23->o2 h24->o2 h25->o2 h26->o2 
##    0.56   -0.18   -3.43    0.16   -0.58   -0.72    0.28   -0.29    0.44 
## h27->o2 h28->o2 h29->o2 h30->o2 h31->o2 h32->o2 h33->o2 h34->o2 h35->o2 
##    0.62    0.28   -0.33    0.21    0.10   -0.62    0.12   -0.24   -0.11 
## h36->o2 h37->o2 h38->o2 h39->o2 h40->o2 h41->o2 h42->o2 h43->o2 h44->o2 
##    0.50   -0.23    0.61   -0.25    0.13    0.30    0.01   -0.12   -0.18 
## h45->o2 h46->o2 h47->o2 h48->o2 h49->o2 h50->o2 
##   -0.04    0.48   -0.19   -0.43    0.59    0.43 
##   b->o3  h1->o3  h2->o3  h3->o3  h4->o3  h5->o3  h6->o3  h7->o3  h8->o3 
##    0.41    0.39    0.85   -0.29   -0.77   -0.53   -0.24    0.60   -1.07 
##  h9->o3 h10->o3 h11->o3 h12->o3 h13->o3 h14->o3 h15->o3 h16->o3 h17->o3 
##    0.05   -0.88   -0.01    0.48   -0.15   -0.33   -0.25    2.22    0.45 
## h18->o3 h19->o3 h20->o3 h21->o3 h22->o3 h23->o3 h24->o3 h25->o3 h26->o3 
##   -0.67    0.37   -0.59   -0.57   -1.15   -0.12   -0.05   -0.35    0.13 
## h27->o3 h28->o3 h29->o3 h30->o3 h31->o3 h32->o3 h33->o3 h34->o3 h35->o3 
##    0.45   -0.02    0.59   -0.22   -0.65   -0.46    0.30   -0.21   -0.12 
## h36->o3 h37->o3 h38->o3 h39->o3 h40->o3 h41->o3 h42->o3 h43->o3 h44->o3 
##    0.44    0.23    0.11   -0.14    0.14   -0.31   -1.65   -0.01    0.64 
## h45->o3 h46->o3 h47->o3 h48->o3 h49->o3 h50->o3 
##    0.26   -1.69   -0.69   -0.09    0.68    0.01

##   accuracy.svm accuracy.rf accuracy.nn
## 1    0.6551812   1.0000000   0.5566616
## 2    0.6193878   0.7285714   0.5704082

将所有的变量加入到预测模型中，对quality进行预测，为了对比效果训练了svm、randomForest、nnet三个模型。
从上述模型训练效果来说，随机森林在测试集上效果最好，准确率达到70%以上。
上述模型没有进行参数调优，效果还有优化空间。
说明quality大体上还是可以通过各个变量来预测的。

另外值得注意的是，随机森林由于搜索空间大，容易出现过拟合。该模型在训练集准确度达到100%，但测试集上的准确率只有72%。可能需要更大量的测试集进一步验证其准确性。

#步骤1：首先将quality按照评分分成三个level，bad, noarmal, good
wineQualityWhites$quality_level = with(wineQualityWhites, 
                                     ifelse(quality_score>6, 'good', 'bad'))
wineQualityWhites$quality_level[wineQualityWhites$quality==6] = 'normal'
wineQualityWhites$quality_level = as.factor(wineQualityWhites$quality_level)

#步骤2：生成训练数据集和测试数据集
set.seed(123)
samp = sample(nrow(wineQualityWhites), 0.8 * nrow(wineQualityWhites))
train = wineQualityWhites[samp, ]
test = wineQualityWhites[-samp, ]

#步骤3：训练svm模型
library(e1071)#加载e1071包
#利用svm建立支持向量机分类模型，采用默认kernel函数rbf
svm.model = svm(quality_level~.-quality-quality_score, data = train[,-1])
summary(svm.model)

#步骤4：效果评估
#训练集效果
confusion.train.svm = table(train$quality_level,
                          predict(svm.model,train,type="class"))
accuracy.train.svm = sum(diag(confusion.train.svm))/sum(confusion.train.svm)

#测试集效果
confusion.test.svm = table(test$quality_level,predict(svm.model,test,type =  "class"))
accuracy.test.svm = sum(diag(confusion.test.svm))/sum(confusion.test.svm)
accuracy.svm = c(accuracy.train.svm, accuracy.test.svm)

#步骤5：同类算法randomForest效果对比
#1 randomForest模型训练
randomForest.model = randomForest(quality_level~.-quality-quality_score, train[,-1])
summary(randomForest.model)
#2 randomForest模型效果评估
#训练集
confusion.train.rf = table(train$quality_level,
                         predict(randomForest.model,train,type = "class"))
accuracy.train.rf = sum(diag(confusion.train.rf))/sum(confusion.train.rf)
#测试集效果
confusion.test.rf = table(test$quality_level,
                        predict(randomForest.model,test,type = "class"))
accuracy.test.rf = sum(diag(confusion.test.rf))/sum(confusion.test.rf)
accuracy.rf = c(accuracy.train.rf,accuracy.test.rf)

#步骤6：同类算法-神经网络效果对比
#1 nnet模型训练
nnet.model = nnet(quality_level~.-quality-quality_score, train[,-1], size = 50, decay = .001)
summary(nnet.model)
#2 nnet模型效果评估
#训练集
confusion.train.nn = table(train$quality_level,
                         predict(nnet.model,train,type = "class"))
accuracy.train.nn = sum(diag(confusion.train.nn))/sum(confusion.train.nn)
#测试集效果
confusion.test.nn = table(test$quality_level,
                        predict(nnet.model,test,type = "class"))
accuracy.test.nn = sum(diag(confusion.test.nn))/sum(confusion.test.nn)
accuracy.nn = c(accuracy.train.nn,accuracy.test.nn)

#步骤7：对比支持向量机、随机森林、人工神经网络算法的准确率
accuracy.data = data.frame(accuracy.svm,accuracy.rf,accuracy.nn)
print(accuracy.data)

4 最终结论与反思

4.1 结论

4.1.1 图1

4.1.1.1 绘图代码

ggplot(data = wineQualityWhites, aes(x = quality, y = alcohol))+
  	   geom_jitter(alpha = 0.3) +
  	   geom_boxplot(alpha = 0.3, color = 'blue')+
	   stat_summary(fun.y = 'mean', geom = 'point', color = 'red')+
	   geom_smooth(method = 'lm', aes(group = 1))+
	   labs(y = 'alcohol (% by volume)',
       title = 'alcohol vs. quality scatter plot')+
	   theme_grey()

4.1.1.2 定稿图

4.1.1.3 结论描述

从图中我们可以发现，酒精浓度越高往往对应的红酒质量越高。

4.1.2 图2

4.1.2.1 绘图代码

ggplot(data = wineQualityWhites, aes(x = alcohol, y = density,color = quality))+
  	   geom_point( alpha = 0.6, size = 1, position = 'jitter')+
  	   scale_color_brewer(type='Qual', palette='Accent',
       guide = guide_legend(title = 'quality', reverse = T,
       override.aes = list(alpha = 1, size = 2)))+
  	   facet_wrap(~quality)+
  	   theme_grey()+
  	   labs(y = "density in (mg/l)", x = 'alcohol (% by volume)',
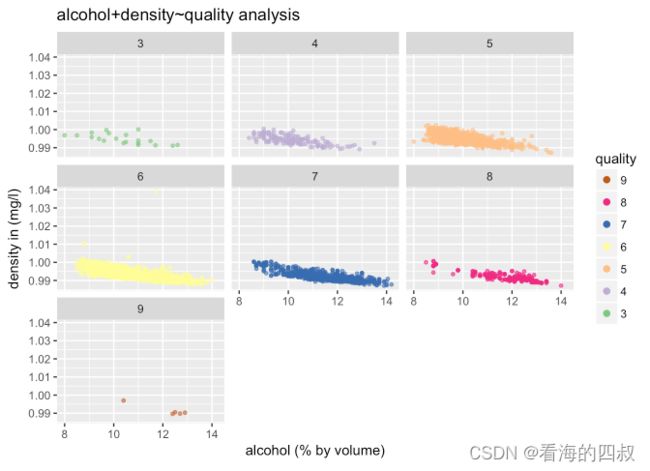
       title = 'alcohol+density~quality analysis')

4.1.2.2 定稿图

4.1.2.3 结论描述

分析发现对于不同quality评分的红酒，几乎都满足随着alcohol提高，红酒的density不断降低的特点。

4.1.3 图3

4.1.3.1 绘图代码

wineQualityWhites$quality_level = with(wineQualityWhites, ifelse(quality_score>6, 'high', 'low')  )
wineQualityWhites$quality_level = factor(wineQualityWhites$quality_level)
ggplot(data = wineQualityWhites, 
       aes(x = residual.sugar, y = density,color = quality_level))+
  	   geom_point( alpha = 0.3, size = 1, position = 'jitter')+
  	   scale_color_brewer(type='Seq', palette='Paired',
       guide = guide_legend(title = 'quality_level', reverse = T,
       override.aes = list(alpha = 1, size = 2)))+
  	   geom_smooth(method = 'lm', se = FALSE, size=1)+
  	   theme_dark()+
  	   labs(x = 'residual.sugar in (g/l)', 
       y = 'density in (g/ml)', 
       title = 'residual.sugar+density~quality analysis')

4.1.3.2 定稿图

4.1.3.3 结论描述

density的主要影响因素是alcohol和residual.sugar。但因为高quality评分[>=7]的葡萄酒的acohol浓度较为集中，低quality评分[<=6]的alcohol浓度较为分散。
因此高quality评分[>=7]白葡萄酒的residual.sugar含量对于density影响更明显，故具有更高的斜率，即residual.sugar含量增加一个单位，density提升的密度量也要更高一些。

4.2 反思

4.2.1 数据分析与模型预测的关系

当一些分析目标比较简单时，可以通过图形绘制、相关性测试来找出数据间的联系。
但如果分析目标的影响因素比较复杂，这个时候就无法通过形象化的图形和简单的相关性测试来找到自变量与预测变量之间的关系。
这个时候就需要更进一步的机器学习算法来进行目标分析。
所以真正要精通数据分析，需要在数据挖掘相关的技能上更进一步。

4.3 写在结尾

好久没写R了，最近要建模故复盘下曾经的项目熟悉熟悉，代码语言得经常练，尤其是多门语言时，不像游泳等生存本能技能长时间不写容易混淆出错，自勉。

原创不易，转载请注意出处：
https://blog.csdn.net/weixin_41613094/article/details/128284695