基于k-means聚类算法的城市出租车GPS时空分布特征分析

目录

前言：

一、研究目的

二、数据源

三、数据预处理

3.1 通用预处理

3.2 删除出租车数据中载客状态瞬间变化的记录

3.3 获取OD数据

3.4 判断每一辆出租车的OD数据中最靠近整点时刻的记录（采用字典形式储存）

3.5 将每一整点时刻出租车的经纬度信息导出成excel文件便于下一步操作

3.6 绘制散点图和GIS分布图查看效果

四、聚类分析

4.1 手工计算（不使用现成的库，使用1点时刻的数据进行测试）

4.2 使用sklearn库进行批量操作

五、数据特征分析

5.1 簇的数量

5.2 簇的分布状况

5.3 簇中的元素数量

5.4 簇的时间分布特征

小结

六、存在的问题

6.1 整点时刻出租车的GPS定位的插值问题

6.2 样本数量问题

6.3 样本时间问题

6.4 （老师点评补充）

七、代码展示

7.1 将数据整理切分成24个时间段

7.2 导入文件绘制散点图

7.3 不同K值选取的对比

7.4 KMeans的计算与可视化

致谢：

参考资料：

---

前言：

本文的内容是“城市大数据分析与应用”课程作业的部分展示，使用的是KMeans聚类算法

一、研究目的

        通过统计各个时间节点上出租车的GPS定位数据，分析各时间城市内不同地块的交通密集程度，为道路改建、城市公共空间节点处理提供理论支撑。通过统计各个时间节点上出租车的GPS定位数据，分析各时间城市内交通密集、人群密集的区域地块分布。为可能的道路改建、城市公共空间节点处理等提供理论支撑。

二、数据源

数据来源：https://people.cs.rutgers.edu/~dz220/data.html

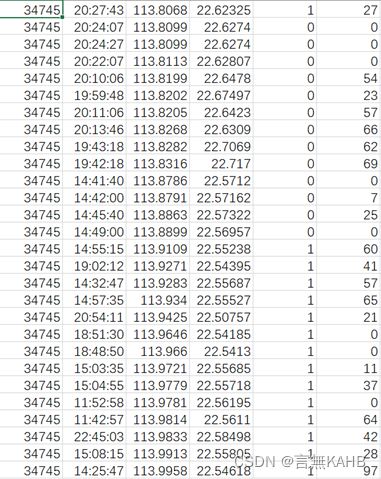
        该表格中六列数据分别为：出租车的编号、时间、经度、纬度、是否空载（0-空载，1-载客）、实时速度。 

三、数据预处理

预处理目标：获取某一编号的车辆在整点时的经纬度，即获取数据的最终形态为[carID, time, longitude, latitude]

3.1 通用预处理

删除信息与前后数据相同的数据以减少数据量

如：某个体连续n条数据除了时间以外其他信息都相同，则可以只保留首末两条数据

transbigdata.clean_same(data, col=['VehicleNum', 'Time', 'Lng', 'Lat'])

3.2 删除出租车数据中载客状态瞬间变化的记录

transbigdata.clean_taxi_status(data, col=['VehicleNum', 'Time', 'OpenStatus'], timelimit=None)

3.3 获取OD数据

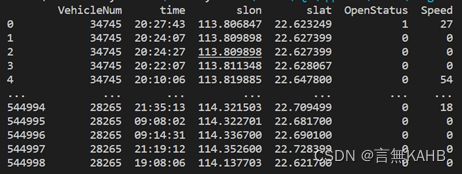
初始数据：

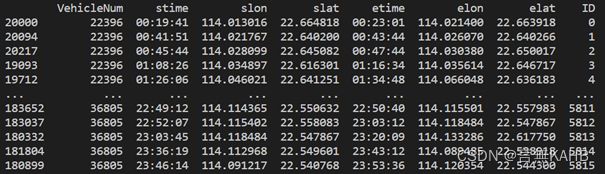
 处理后数据：

选择OD数据作为经纬度获取的基准

3.4 判断每一辆出租车的OD数据中最靠近整点时刻的记录（采用字典形式储存）

注意： 由于初始数据中时间均不是整点时刻，本次研究中是粗略地将最靠近整点时刻的时间点的经纬度作为目标经纬度，如果需要推断整点时刻的经纬度，则需要做插值运算，若采用线性插值，则会出现插值的点坐标不在道路上的情况（实际上这种情况下可以将该插值点投影到最近道路上，这里由于道路信息缺失未加以考虑）。

3.5 将每一整点时刻出租车的经纬度信息导出成excel文件便于下一步操作

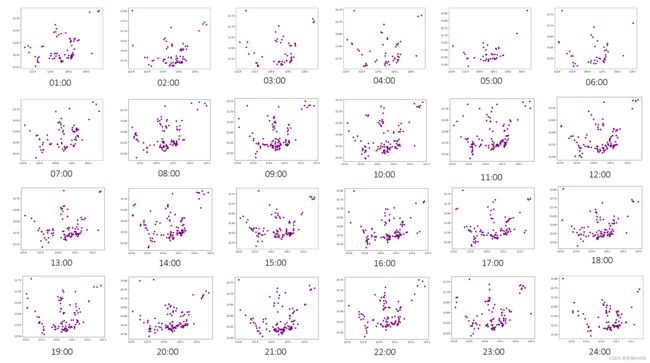
3.6 绘制散点图和GIS分布图查看效果

 

四、聚类分析

4.1 手工计算（不使用现成的库，使用1点时刻的数据进行测试）

此处写了一段递归算法，使用KMeans聚类算法的原始定义进行迭代，其基本流程为：根据给定的K值随机选取原数据点作为初始质心（initCenters）——计算每个点到初始质心的距离，按照最近距离来划分簇——根据划分完成的簇计算新的质心（newCenters）——判断新的质心是否与初始质心一致，若一致，测结束递归，完成聚类；若不一致，则将新的质心赋给初始质心再次迭代。

randomNum = np.random.randint(0,len(xx),size=k)
initCenters = []
for i in randomNum:
    initCenters.append(xx[i])
# 计算每个点和初始中心点的距离
datalen = len(xx)
target = np.full(shape=datalen, fill_value=-1)
def updateCenters(initCenters, counter, limit):
    for i in range(len(xx)):
        dis = []
        for j in range(k):
            dis.append(distance(xx[i],initCenters[j]))
        target[i] = np.argmin(dis)
    newCenters = []
    for i in range(k):
        mean = []
        for j in range(len(xx)):
            if(target[j] == i):
                mean.append(xx[j])
        newCenters.append(np.mean(mean,axis=0))
    if(counter == 0):
        print('未收敛，当前迭代次数为：'+str(limit - counter))
        plt.scatter(x,y,c=target)
        plt.show()
    else:
        if(np.array(newCenters) == initCenters).all():
            print('已收敛，迭代次数为：'+str(limit - counter))
            plt.scatter(x,y,c=target)
            plt.show()
        else:
            counter = counter - 1
            initCenters = np.array(newCenters)
            updateCenters(initCenters, counter, limit)
updateCenters(initCenters,5,5)

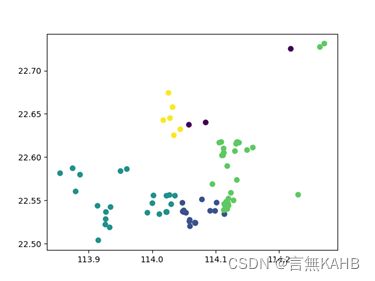
（迭代次数为1次，K值根据目测给出5）

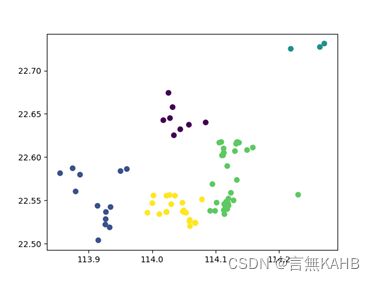
（迭代次数为3次，K值根据目测给出5，此时聚类已收敛） 

（*根据测试来看，迭代次数一般不超过10次即可收敛）

4.2 使用sklearn库进行批量操作

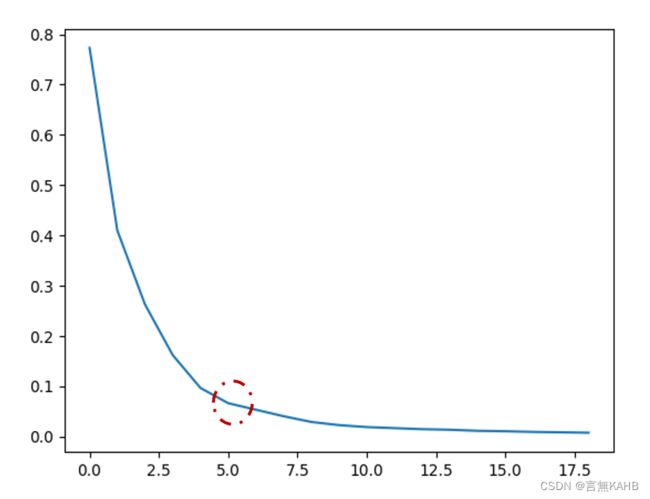
在批量操作之前，需要考虑应该使用怎样的K值，在这里需要计算不同K值情况下的误差平方和SSE（Sum of Square Error），用于计算最佳K值。

注：SSE的计算方法：计算每一个K值情况下，各点到其聚类质心的距离的平方和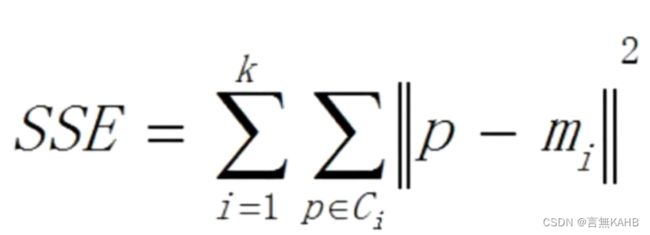

（p为点，m为各聚类中心） 

下面以1点时刻为例：

这里我们选取K值等于5，由此得到下图：

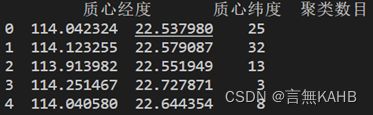
同时计算各簇质心和聚类数目

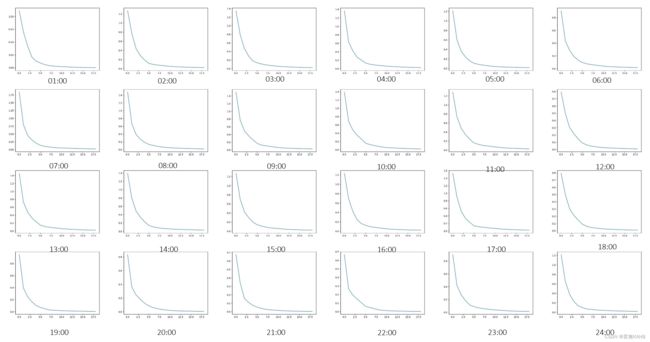
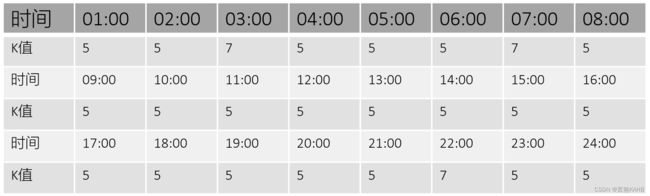
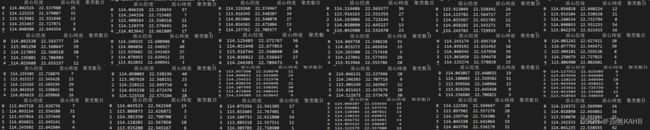
 以此类推，计算24个小时的K值情况

由上图可得最佳K值的选择情况以及质心经纬度、聚类数目

 

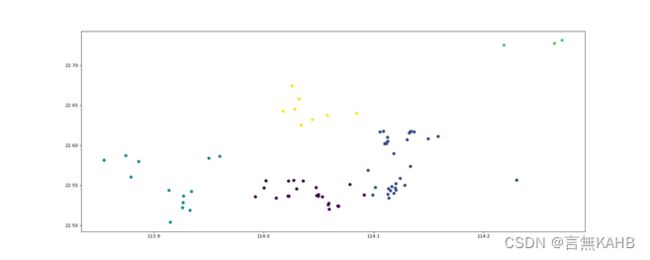
 然后根据上表选择的K值绘制聚类图

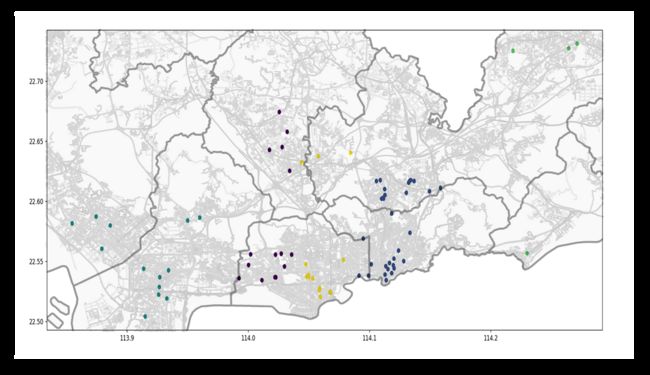
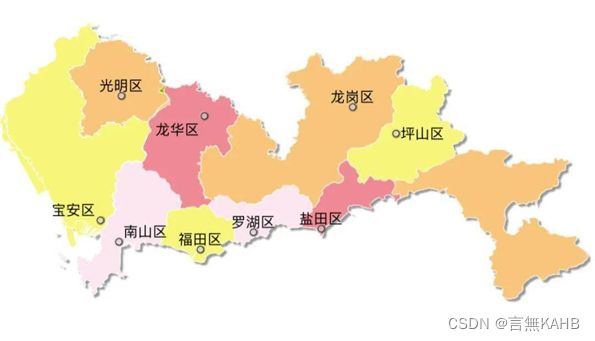
将聚类图叠到深圳市行政地图上可得下图 

（1点的聚类情况） 

聚类运算完毕 

五、数据特征分析

从聚类结果可以看出：

5.1 簇的数量

按聚类簇的数量来看，大多数时间段的簇都是5个（部分为7个），因此可以大致推断出深圳人群较为密集的区域有5到7个，即“核心区域”。

5.2 簇的分布状况

按聚类簇的分布状况来看，该5到7个核心区域分别为：

  ①腾讯滨海大厦周边

  ②车公庙--深圳市政府附近

  ③深圳火车站—深圳万象城附近

  ④深圳北站—南方科技大学片区

  ⑤深圳东站片区

  ⑥龙城广场（龙岗区中心地带）

  ⑦宝安国际机场片区

5.3 簇中的元素数量

按聚类簇中元素的数量来看，

  数量最多的簇对应的地块为深圳火车站—深圳万象城附近；数量略次一些的为腾讯滨海大厦周边和车公庙—深圳市政府附近。反映出这三个地块是人群最密集、人流量最大的三个片区。

5.4 簇的时间分布特征

按聚类簇的时间分布特征来看，

  1点至7点期间，簇的分布较为分散，可以从SSE分布曲线中看出，SSE值相对较大，说明此时各要素分布较为离散。

  8点至11点期间，簇的分布较为集中。主要集中在南山区腾讯大厦片区、深圳火车站、深圳市政府—深圳东站三个区域。

  12点至14点期间，北侧一个簇有向南侧整体偏移的趋势，即龙华区北侧人群向龙华区中心、南侧靠拢的趋势。

  15点至18点期间，簇的分布有从福田区深圳市政府向外扩散的趋势。推测是下班人群从市中心向外流动导致。

  19点至22点期间，簇的分布总体较为平稳均匀。

  23点至24点期间，簇的分布与1点至7点类似，较为分散，仅在深圳站、深圳东站片区较为集中。

小结

总体来看，簇的时间分布在深圳几个火车站周边变动较小，一天24小时都有人群在此处聚集；而南山区、福田区作为主要的工作生活区域，随着时间变化有较为明显的随时间变动的簇的偏移，说明了人群的周期性活动。此外，簇的分布整体呈东西向布局。与城市形状相吻合；簇的变化运动以东西向为主，南北向较少，这也与深圳东西向交通发达，南北向交通较为不变相符。 

六、存在的问题

6.1 整点时刻出租车的GPS定位的插值问题

      如果按照线性插值的方法计算可能会导致定位坐标不在街道上，因此在本研究中采用了最近时刻的位置替代，使数据产生了误差。

6.2 样本数量问题

        本研究中初始数据共有545000条数据，经过筛选和OD处理之后每个整点时刻可用的坐标定位下降到100条左右，在做单独时刻的聚类分析时数据量仍显不足。

6.3 样本时间问题

      本研究中初始数据为2013年10月22日星期二，一方面该数据时间较为久远，对目前的参考价值有限；另一方面，该日期为工作日，需要补充休息日的数据作为进一步分析支撑。

6.4 （老师点评补充）

可以补充其他非一线城市的数据情况分析；

可以补充其他出行方式的GPS数据（公交车、共享单车等）；

可以补充分析现在的GPS数据做疫情前后的对比分析。

七、代码展示

7.1 将数据整理切分成24个时间段

from time import time
from sklearn.metrics import accuracy_score
import transbigdata as tbd
import pandas as pd
import geopandas as gpd
import math
import xlwt

data = pd.read_csv('TaxiData-Sample.csv',header=None)
data.columns = ['VehicleNum','time','slon','slat','OpenStatus','Speed']

oddata = tbd.taxigps_to_od(data,col = ['VehicleNum','time','slon','slat','OpenStatus'])
#print(oddata)

solvedTable = {}
match = []
matchAll = []
counter = 0
init_num = 22396
init_time = 0
absTemp = []
for i in range(5815):
    if(oddata.iloc[i]['VehicleNum'] == init_num):
        # counter = counter + 1
        # 找距离该时间点最近的整数时间点
        hour = oddata.iloc[i]['stime'][0]+oddata.iloc[i]['stime'][1]
        minute = oddata.iloc[i]['stime'][3]+oddata.iloc[i]['stime'][4]
        second = oddata.iloc[i]['stime'][6]+oddata.iloc[i]['stime'][7]
        time = round(int(hour) + int(minute) / 60 + int(second) / 600,2) #将时间转换成小数表示
        adj_time = round(time,0) # 四舍五入取整

        if(adj_time == init_time):
            difference = abs(round(adj_time - time,2)) # 求差值            
            absTemp.append(difference)
        else:
            if(len(absTemp) == 1):
                new_log = oddata.iloc[i-1]['slon']
                new_lat = oddata.iloc[i-1]['slat']
                match.append(init_time)
                match.append(new_log)
                match.append(new_lat)
            elif(len(absTemp) > 1):
                absDup = absTemp
                absTemp.sort()
                for j in range(len(absTemp)):
                    if(absDup[j] == absTemp[0]):
                        new_log = oddata.iloc[i+j+1-len(absTemp)]['slon']
                        new_lat = oddata.iloc[i+j+1-len(absTemp)]['slat']
                        match.append(init_time)
                        match.append(new_log)
                        match.append(new_lat)
            absTemp = []
            init_time =  adj_time
            difference = abs(round(adj_time - time,2)) # 求差值            
            absTemp.append(difference)
            matchAll.append(match)
            match = []

    else:
        #match.append(counter)
        solvedTable[str(init_num)] = matchAll
        matchAll = []
        counter = 1
        init_num = oddata.iloc[i]['VehicleNum']

#print(solvedTable)
datalist = []
interval = 16
for i,j in solvedTable.items():
    for k in j:
        if(k[0] == interval):
            datalist.append([int(i), k[1], k[2]])
book = xlwt.Workbook(encoding='utf-8',style_compression=0)
sheet = book.add_sheet('Taxi_' + str(interval),cell_overwrite_ok=True)
col = ('carID','longitude','latitude')
for i in range(0,3):
        sheet.write(0,i,col[i])
#datalist = [[0,0,0],[1,1,1]]
for i in range(0,len(datalist)):
        data = datalist[i]
        for j in range(0,3):
            sheet.write(i+1,j,data[j])
savepath = 'E:/Urban/Taxi_' + str(interval) + '.xls'
book.save(savepath)

7.2 导入文件绘制散点图

import matplotlib.pyplot as plt
import pandas as pd
import xlrd

#读入文件
file_path = "visual/Taxi_24.xls"
df = pd.read_excel(file_path, header=None)

#print(df)
#定义 x  y变量
x = []
y = []

#定义颜色变量
color = ['c', 'b', 'g', 'r', 'm', 'y', 'k', 'w']

#用for循环将文件中的值赋值给x，y
for i in range(1,len(df[0])):
    x.append(df[1][i])
    y.append(df[2][i])

#画图
plt.scatter(x, y, c=color[1], edgecolors='r')
plt.show()

7.3 不同K值选取的对比

import matplotlib.pyplot as plt
from prometheus_client import Metric
from pyrsistent import l
from sklearn import preprocessing
from sklearn import cluster
from sklearn.datasets._samples_generator import make_blobs
from sklearn.cluster import KMeans, linkage_tree
from sklearn.metrics import calinski_harabasz_score
import pandas as pd
import time
import numpy as np
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import AgglomerativeClustering

def calSSE(data,target,k):
    sse = 0
    clusterI = []
    for i in range(k):        
        for j in range(len(target)):
            if(target[j] == i):
                clusterI.append(data[j])

        m = np.mean(clusterI, axis = 0)
        for p in clusterI:
            sse += np.sum(np.square(p-m))
        
        clusterI = []
   
    return sse

for v in range(25):
    #读入文件
    file_path = "visual/Taxi_"+str(v)+".xls"
    df = pd.read_excel(file_path, header=None)
    x = []
    y = []
    for i in range(1,len(df[0])):
        x.append(df[1][i])
        y.append(df[2][i])

    xx = []
    # k = 5
    for i in range(len(x)):
        xx.append([x[i],y[i]])
    #mod = KMeans(n_clusters=k,random_state=9)
    #y_pre = mod.fit_predict(xx)

    #print(calSSE(xx,y_pre,k))
    arr = []
    for k in range(1,20):
        kms = KMeans(n_clusters=k)
        y_pre = kms.fit_predict(xx)
        arr.append(calSSE(xx,y_pre,k))

    plt.plot(arr)
    plt.show()

7.4 KMeans的计算与可视化

import matplotlib.pyplot as plt
from prometheus_client import Metric
from pyrsistent import l
from sklearn import preprocessing
from sklearn.datasets._samples_generator import make_blobs
from sklearn.cluster import KMeans, linkage_tree
from sklearn.metrics import calinski_harabasz_score
import pandas as pd
import time
import numpy
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import AgglomerativeClustering

file_path = "visual/Taxi_22.xls"
df = pd.read_excel(file_path, header=None)
x = []
y = []
for i in range(1,len(df[0])):
    x.append(df[1][i])
    y.append(df[2][i])

xx = []
mod = KMeans(n_clusters=7,random_state=9)
for i in range(len(x)):
    xx.append([x[i],y[i]])
y_pre = mod.fit_predict(xx)
plt.figure(figsize=(20,8),dpi=80)
plt.scatter(x,y,c=y_pre)
plt.show()

r1 = pd.Series(mod.labels_).value_counts()
r2 = pd.DataFrame(mod.cluster_centers_)
r = pd.concat([r2, r1], axis = 1)
r.columns = ['质心经度','质心纬度','聚类数目']
print(r)

致谢：

感谢王老师一学期的付出，在线上上课的情况下克服重重困难为我们带来精彩的课程内容！

参考资料：

[1] 【数学建模】聚类分析——python实现_Fonsi-的博客-CSDN博客_聚类分析python

[2] python数据分析：聚类分析（cluster analysis）_泛泛之素的博客-CSDN博客_python聚类分析

[3] python 聚类_10种Python聚类算法完整操作示例（建议收藏）_ASS-ASH的博客-CSDN博客_python 聚类

[4] 数据挖掘复习笔记之聚类&关联 - 知乎 

[5] 聚类分析_哔哩哔哩_bilibili