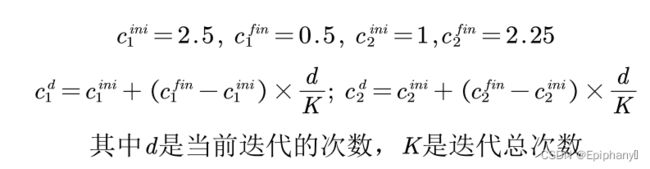粒子群算法

粒子群算法简介

粒子群算法，其全称为粒子群优化算法(Particle Swarm Optimization,PSO) 。它是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的搜索算法。粒子群算法属于启发式算法也叫智能优化算法，其基本思想在于通过群体中个体之间的协作和信息共享来寻找最优解。

1995年，美国学者Kennedy和Eberhart共同提出了粒子群算法，其基本思想源于对鸟类群体行为进行建模与仿真的研究结果的启发。它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的可行解。

应用场景：TSP这类组合优化问题、非线性整数规划问题、函数优化、神经网络训练、模糊系统控制以及其它遗传算法的应用邻域。

粒子群算法当中的基本概念

粒子：优化问题的候选解

位置：候选解所在的位置

速度：候选解移动的速度

适应度：评价粒子优劣的值，一般设置为目标函数值

个体最佳位置：单个粒子迄今为止找到的最佳位置

群体最佳位置：所有粒子迄今为止找到的最佳位置

原理

来源粒子群算法简单介绍 - 简书 (jianshu.com)

粒子群算法初始化为一群随机的粒子（随机解），然后根据迭代找到最优解。每一次迭代中，粒子通过跟踪两个极值来更新自己：第1个是粒子本身所找到的最优解，这个称为个体极值；第2个是整个种群目前找到的最优解，这个称为全局极值。也可以不用整个种群，而是用其中的一部分作为粒子的邻居，称为局部极值。

假设在一个D维搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量：

$X_i=(x_{i1},x_{i2},\dots ,x_{iD}),i=1,2,\dots ,N$

第i个粒子的速度表示为：

$V_i=(v_{i1},v_{i2},\dots ,v_{iD}),i=1,2,\dots ,N$

还要保存每个个体的已经找到的最优解$p_{best}$，和一个整个群落找到的最优解$g_{best}$。

第i个粒子根据下面的公式更新自己的速度和位置：

$v_{id}=w\times v_{id-1}+c_1{r}_1(p_{id}-x_{id})+c_2{r}_2(p_{gd}-x_{id})$

该式由三部分组成，分别为

1. 惯性或动量部分，反应粒子的运动习惯。
2. 认知部分，粒子有向自身历史最佳位置逼近的优势。
3. 社会部分，粒子有向群体或领域历史最佳位置逼近的趋势

公式解释：这个粒子第d步的速度=上一步自身的速度惯性+自我认知部分+社会认知部分（三个部分的和）

$x_{id+1}=x_{id}+v_{id}$

这个粒子第d+1步所在的位置 = 第d步所在的位置 + 第d步的速度 * 运动的时间

x(d+1) = x(d) + v(d) * t (每一步运动的时间t一般取1)

其中，$P_{id}$是个体已知最优解，$p_{gd}$是种群已知最优解 ,$w$为惯性权重，, $c_1$ $c_2$为学习因子（或加速常数 acceleration constant)，$r_1{r}_2$是[0,1]范围内的随机数。

在最初提出粒子群算法的论文中指出，个体学习因子和社会(或群体)学习因子取2比较合适

惯性权重w体现的是粒子继承先前的速度的能力，Shi,Y最先将惯性权重w引入到粒子群算法中，并分析指出一个较大的惯性

权值有利于全局搜索，而一个较小的权值则更利于局部搜索

一个简单的例子

求二元函数的最小值

求函数$y=x_1^2+x_2^2-x_1{x}_2-10x_1-4x_2+60$在$x_1,x_2\in [-15,15]$内的最小值

用粒子群算法求解函数最小值时，粒子适应度的计算设置为目标函数值，但是此时我们希望找到适应度最小的解。

%% 粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示）
clear; clc

%% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on  % 不关闭图形，继续在上面画图

%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
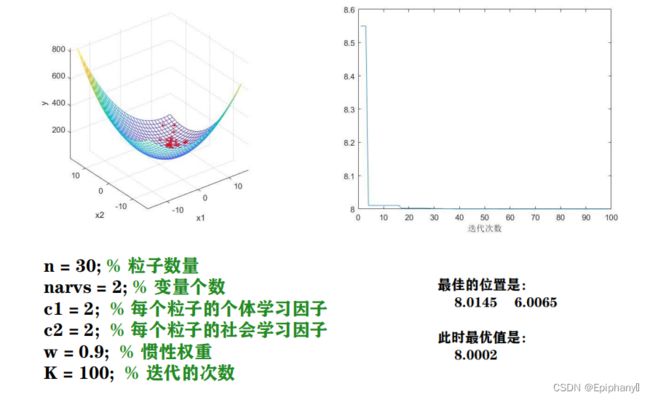
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 100;  % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界

%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs);  % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）

%% 计算适应度(注意，因为是最小化问题，所以适应度越小越好)
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun2(x(i,:));   % 调用Obj_fun2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

%% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）

%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) < Obj_fun2(pbest(i,:))   % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) < Obj_fun2(gbest)  % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun2(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
    h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end

figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun2(gbest))

运算结果呈现

资料来源于数学建模清风课件

粒子群算法的改进

线性递减惯性权重，能够更好的平衡算法的全局搜索以及局部搜索能力

自适应惯性权重，与原来的相比，现在的惯性权重和迭代次数与每个粒子的适应度有关。

随机惯性权重，使用随机的惯性权重，可以避免在迭代前期局部搜索能力的不足；也可以避免在迭代后期全局搜索能力的不足

压缩因子法

非对称学习因子

自动退出迭代循环，当粒子已经找到最佳位置后，再增加迭代次数只会浪费计算时间，那么我们能否设计一个策略，能够自动退出迭代呢

在迭代的过程中，每次计算出来最佳适应度后，都计算该适应度和上一次迭代时最佳适应度的变化量(取绝对值)；判断这个变化量和“函数变化量容忍度”的相对大小，如果前者小，则计数器加1；否则计数器清0；不断重复这个过程，有以下两种可能

① 此时还没有超过最大迭代次数，计数器的值超过了最大计数值，那么我们就跳出迭代循环，搜索结束。
② 此时已经达到了最大迭代次数，那么直接跳出循环，搜索结束。