如何理解向量化的梯度函数,矩阵化的theta西塔θ
黄海广博士在(吴恩达)机器学习课程练习3(ML-Exercise3)中,重写逻辑回归中梯度函数的实现,改为完全向量化(即没有“for”循环)
向量化前的梯度函数(“for”循环模式):
def gradient_with_loop(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i])
if (i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad
向量化后的梯度函数:
def gradient(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
error = sigmoid(X * theta.T) - y
grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)
# intercept gradient is not regularized
grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)
return np.array(grad).ravel()
我在做第一节和第二节练习题时,就发现for循环可以直接用矩阵乘法代替,一开始还纳闷黄博士和其他答案提供者为何不用向量法,难道没有发现这种方法又简洁便利又高级。实际上后来觉察到他们这样写一定是故意的,是为了结合公式推导,并且为以后升级埋下伏笔。果然在这里应验了。
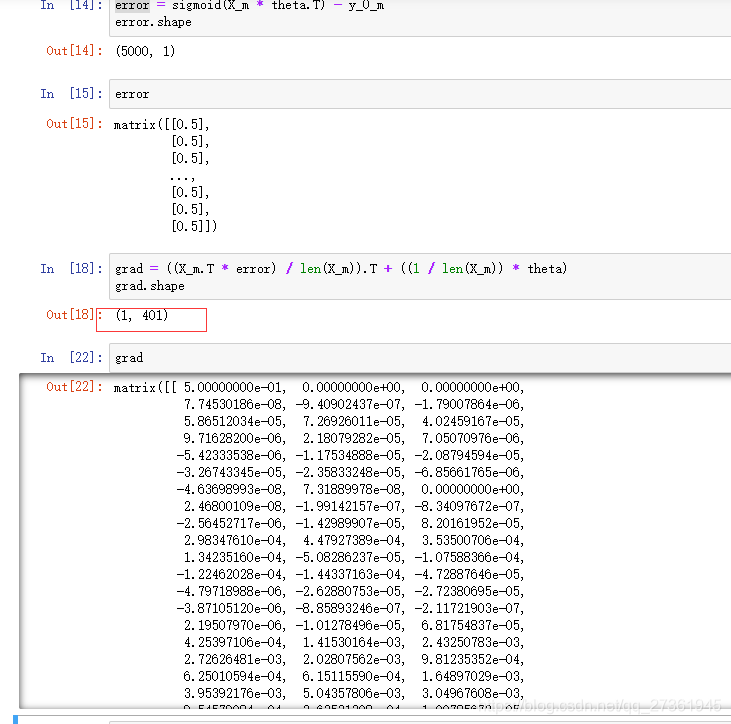
仔细看了一下向量化后的代码,第6行和我的预期基本一致:
grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)
第七行计算权值参数 θ 0 θ_0 θ0导数的地方用grad[0, 0]表示,而非grad[0],让我感到困惑,这表示θ的导数是个矩阵,而不是单行向量:
grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)
这说明θ也是个矩阵(当时我没有注意grad是导数,就把grad当成权值参数θ了)
权值参数θ从单行向量变成矩阵,那是怎么回事,是因为y从单个值(单行向量)变成多个值(矩阵)
凡是涉及到多个矩阵乘法,就让人晕头。
开始把θ矩阵理解为神经网络每层一个θ向量,组合起来得到一个矩阵:
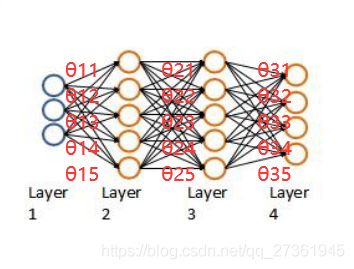
但问题是X只能与第一层的θ相乘得到第二次的输入,不可能与第二层以后的θ相乘得到y。
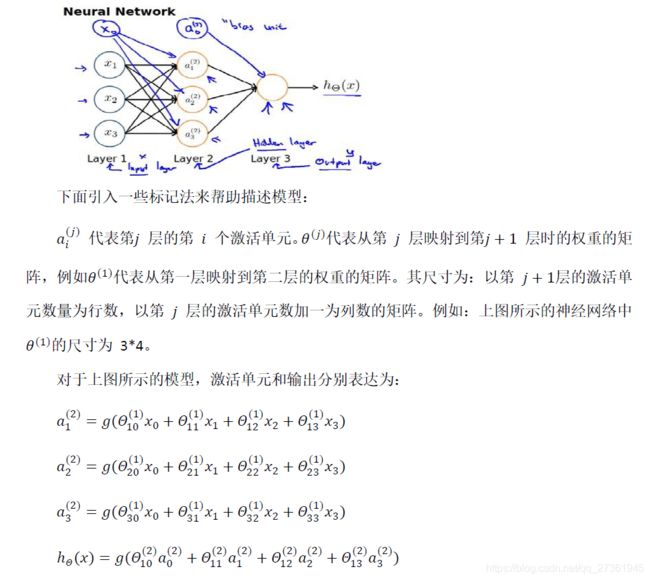
在这里找到θ明确的定义,原来θ只能代表相邻两层之间的传递权值参数(吐槽下,老师为了省事,在那张本来就有很多线的神经网络示意图上写写画画,想标明哪条线是 θ 11 θ_{11} θ11,哪条线是 θ 12 θ_{12} θ12,太图省事了,他心里清楚,但是学的人要是不懂,根本看不清,想看清必须擦掉多余的线。)
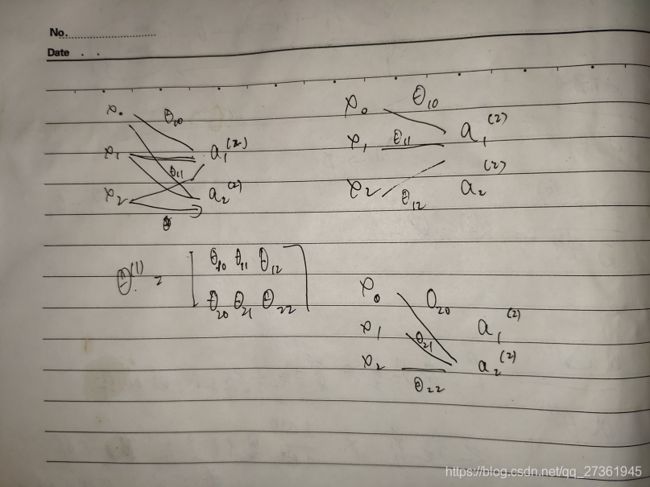
θ矩阵中,第一行θ都是指向 a 1 a_1 a1 ( y 1 y_1 y1)的,第二行都指向 a 2 a_2 a2 ( y 2 y_2 y2)
这样就清晰了,原来多层神经网络,需要分别计算每层的输出 a ( 1 ) a^{(1)} a(1),即h(x)=g(X· θ T θ^T θT),再用 a ( 1 ) a^{(1)} a(1)结果作为下一层的输入 X ( 2 ) X^{(2)} X(2),计算下一层的输出 a ( 2 ) a^{(2)} a(2)
所以神经网络(前向传播和反向传播)的运算量是惊人的。
在截稿前,我又发现个问题:只有grad[0, 0]不受正则化影响,正常情况下grad[1, 0]、grad[2, 0]、…grad[i, 0]都不受正则化影响,感觉这里是为了提高算法效率做了优化。只针对grad[0, 0]不做正则化处理,不影响实际计算结果。(我猜的)
我猜错了,X是(5000,400),表示5000个400维向量,不是5000个20×20矩阵。所以 x 0 x_0 x0只有1个,最笨的办法全列出来是: x 0 x_0 x0, x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x 400 x_{400} x400。
grad是一个1×400矩阵,所以不是数组,所以第一个元素用grad[0, 0]表示,而不是grad[0]。原来并不是我想的多输出y,y只有一个,不存在grad[1:, :],不存在grad[1, 0]、grad[2, 0]、…grad[i, 0],grad没有多行,grad只有1行。
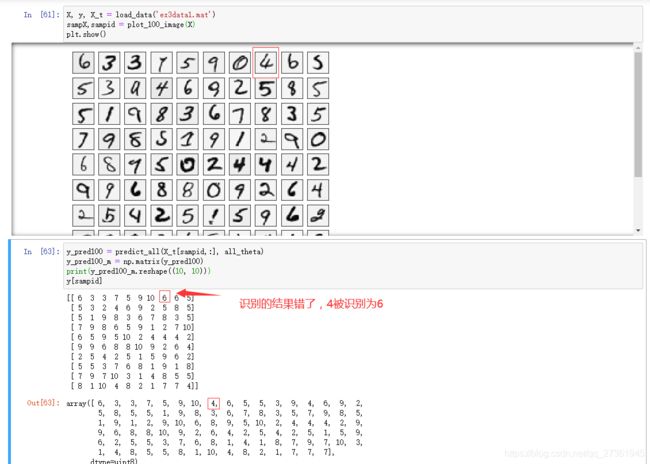
经过魔改,对比机器识别结果和原始值,能看出第一行倒数第三个数4被错误识别为6: