GAN 系列的探索与pytorch实现 (数字对抗样本生成)

GAN 系列的探索与pytorch实现 (数字对抗样本生成)

GAN的简单介绍

生成对抗网络（英语：Generative Adversarial Network，简称GAN）是非监督式学习的一种方法，通过让两个神经网络相互博弈的方式进行学习。该方法由伊恩·古德费洛等人于2014年提出。生成对抗网络由一个生成网络与一个判别网络组成。生成网络从潜在空间（latent space）中随机取样作为输入，其输出结果需要尽量模仿训练集中的真实样本。判别网络的输入则为真实样本或生成网络的输出，其目的是将生成网络的输出从真实样本中尽可能分辨出来。而生成网络则要尽可能地欺骗判别网络。两个网络相互对抗、不断调整参数，最终目的是使判别网络无法判断生成网络的输出结果是否真实。

生成对抗网络常用于生成以假乱真的图片。此外，该方法还被用于生成影片、三维物体模型等。

虽然生成对抗网络原先是为了无监督学习提出的，它也被证明对半监督学习、完全监督学习、强化学习是有用的。在一个2016年的研讨会，杨立昆描述生成式对抗网络是“机器学习这二十年来最酷的想法”。

若想仔细的了解一下，具体的介绍和应用都在一文看懂「生成对抗网络 - GAN」基本原理+10种典型算法+13种应用中有详细的介绍

生成对抗网络 GAN 的基本原理

大白话版本

知乎上有一个很不错的解释，大家应该都能理解：

假设一个城市治安混乱，很快，这个城市里就会出现无数的小偷。在这些小偷中，有的可能是盗窃高手，有的可能毫无技术可言。假如这个城市开始整饬其治安，突然开展一场打击犯罪的「运动」，警察们开始恢复城市中的巡逻，很快，一批「学艺不精」的小偷就被捉住了。之所以捉住的是那些没有技术含量的小偷，是因为警察们的技术也不行了，在捉住一批低端小偷后，城市的治安水平变得怎样倒还不好说，但很明显，城市里小偷们的平均水平已经大大提高了。

警察们开始继续训练自己的破案技术，开始抓住那些越来越狡猾的小偷。随着这些职业惯犯们的落网，警察们也练就了特别的本事，他们能很快能从一群人中发现可疑人员，于是上前盘查，并最终逮捕嫌犯；小偷们的日子也不好过了，因为警察们的水平大大提高，如果还想以前那样表现得鬼鬼祟祟，那么很快就会被警察捉住。

为了避免被捕，小偷们努力表现得不那么「可疑」，而魔高一尺、道高一丈，警察也在不断提高自己的水平，争取将小偷和无辜的普通群众区分开。随着警察和小偷之间的这种「交流」与「切磋」，小偷们都变得非常谨慎，他们有着极高的偷窃技巧，表现得跟普通群众一模一样，而警察们都练就了「火眼金睛」，一旦发现可疑人员，就能马上发现并及时控制——最终，我们同时得到了最强的小偷和最强的警察。

非大白话版本

生成对抗网络（GAN）由2个重要的部分构成：

1. 生成器(Generator)：通过机器生成数据（大部分情况下是图像），目的是“骗过”判别器
2. 判别器(Discriminator)：判断这张图像是真实的还是机器生成的，目的是找出生成器做的“假数据”

下面详细介绍一下过程：

第一阶段：固定「判别器D」，训练「生成器G」

我们使用一个还 OK 判别器，让一个「生成器G」不断生成“假数据”，然后给这个「判别器D」去判断。

一开始，「生成器G」还很弱，所以很容易被揪出来。

但是随着不断的训练，「生成器G」技能不断提升，最终骗过了「判别器D」。

到了这个时候，「判别器D」基本属于瞎猜的状态，判断是否为假数据的概率为50%。

第二阶段：固定「生成器G」，训练「判别器D」

当通过了第一阶段，继续训练「生成器G」就没有意义了。这个时候我们固定「生成器G」，然后开始训练「判别器D」。

「判别器D」通过不断训练，提高了自己的鉴别能力，最终他可以准确的判断出所有的假图片。

到了这个时候，「生成器G」已经无法骗过「判别器D」。

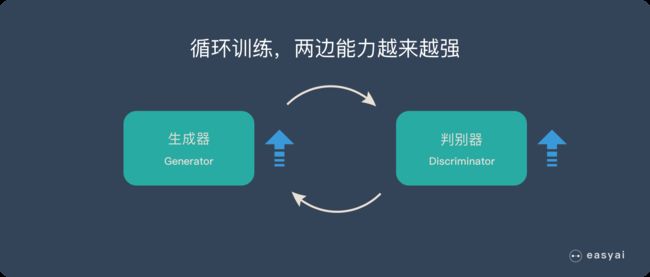
循环阶段一和阶段二

通过不断的循环，「生成器G」和「判别器D」的能力都越来越强。

最终我们得到了一个效果非常好的「生成器G」，我们就可以用它来生成我们想要的图片了。

下面的实际应用部分会展示很多“惊艳”的案例。

如果对 GAN 的详细技术原理感兴趣，可以看看下面2篇文章：

《生成性对抗网络（GAN）初学者指南 – 附代码》

《长文解释生成对抗网络GAN的详细原理（20分钟阅读）》

数字对抗样本产生

首先简要看一下我们的实验

LeNet是一个小型的神经网络结构，仅包含两层卷积层、两个池化层以及三层全连接。该轻量级网络能快速、占内存小、高精确度的解决复杂度比较低的问题，如手写数字识别。本实验要求：

• (步骤1)用LeNet网络完成手写数字识别任务。
• (步骤2)利用对抗样本工具包生成针对该网络的对抗样本。

步骤1：用LeNet网络完成手写数字识别任务。

---

LeNet 网络

在之前VGG的介绍中，我们介绍了一个ILSVRC比赛，当时说我们的VGG是14年的亚军，但是在之前，LetNet曾统治过一个时代。LeNet-5是较早的一个卷积神经网络，在1998年的时候被提出。这个网络一大特点，是那时候计算机处理速度不快，因此网络整个的设计都比较小，总参数约6万个。

开山之作：LeNet

LetNet是卷积神经网络的祖师爷LeCun在1998年提出，用于解决手写数字识别的视觉任务。自那时起，CNN的最基本的架构就定下来了：卷积层、池化层、全连接层。如今各大深度学习框架中所使用的LeNet都是简化改进过的LeNet-5（-5表示具有5个层），和原始的LeNet有些许不同，比如把激活函数改为了现在很常用的ReLu。

可以说，它定义了CNN的基本组件，是CNN的鼻祖。

LeNet-5跟现有的conv->pool->ReLU的套路不同，它使用的方式是conv1->pool->conv2->pool2再接全连接层，但是不变的是，卷积层后紧接池化层的模式依旧不变。

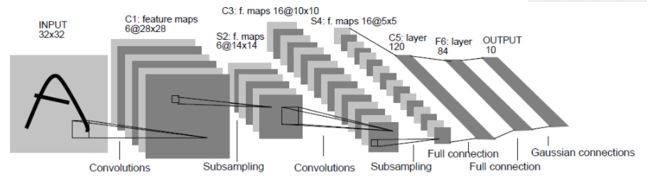
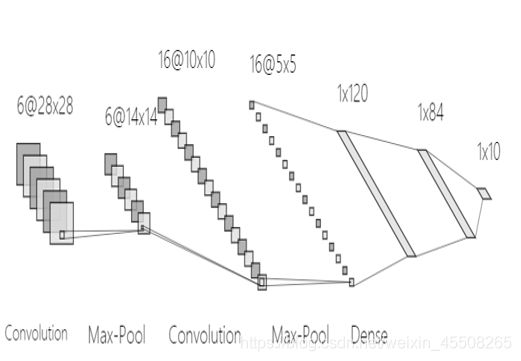
以上图为例，对经典的LeNet-5做深入分析：

1. 首先输入图像是单通道的28*28大小的图像，用矩阵表示就是[1,28,28]
2. 第一个卷积层conv1所用的卷积核尺寸为5*5，滑动步长为1，卷积核数目为20，那么经过该层后图像尺寸变为24，28-5+1=24，输出矩阵为[20,24,24]。
3. 第一个池化层pool核尺寸为2*2，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为12×12，输出矩阵为[20,12,12]。
4. 第二个卷积层conv2的卷积核尺寸为5*5，步长1，卷积核数目为50，卷积后图像尺寸变为8,这是因为12-5+1=8，输出矩阵为[50,8,8].
5. 第二个池化层pool2核尺寸为2*2，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为4×4，输出矩阵为[50,4,4]。
6. pool2后面接全连接层fc1，神经元数目为500，再接relu激活函数。
7. 再接fc2，神经元个数为10，得到10维的特征向量，用于10个数字的分类训练，送入softmaxt分类，得到分类结果的概率output。

数据集的下载和预处理

这里我们用的都是经典的数据集，也就是minst数据集，并且我们可以利用torchvision，他还提供了transforms类可以用来正规化处理数据。

# mean = 0.5
# std = 0.5
mean = 0.1307
std = 0.3081
transformtion = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((mean,),(std,))]
)

train_dataset = datasets.MNIST('./mnist',train=True,transform = transformtion, download=True)
test_dataset = datasets.MNIST('./mnist',train=False,transform = transformtion, download=True)

train_loader = torch.utils.data.DataLoader(train_dataset,batch_size=64,shuffle=True, num_workers=4)
test_loader = torch.utils.data.DataLoader(test_dataset,batch_size=64,shuffle=True, num_workers=4)

len(train_dataset),len(test_dataset)

(60000, 10000)

我们可以看到我们的训练数据集有60000个，测试数据集有10000个

Image displaying

import matplotlib.pyplot as plt
def plot_img(image):
    image = image.numpy()[0]
    # print(image.shape)
    image = ((mean * image) + std)
    plt.imshow(image ,cmap='gray')

images, label =  next(iter(train_loader))
img = torchvision.utils.make_grid(images)
img= img.numpy().transpose(1,2,0)
img = img*std + mean
plt.imshow(img)

pytorch 搭建LeNet

在前面我们已经粗略的介绍了一下我们的LeNet，现在我们就可以用Pytorch来搭建我们的LeNet模型

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        
        # 输入 1 * 28 * 28
        self.conv = nn.Sequential(
            # 卷积层1
            # 在输入基础上增加了padding，28 * 28 -> 32 * 32
            # 1 * 32 * 32 -> 6 * 28 * 28
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), nn.ReLU(),
            # 6 * 28 * 28 -> 6 * 14 * 14
            nn.MaxPool2d(kernel_size=2, stride=2), # kernel_size, stride
            # 卷积层2
            # 6 * 14 * 14 -> 16 * 10 * 10 
            nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5), nn.ReLU(),
            # 16 * 10 * 10 -> 16 * 5 * 5
            nn.MaxPool2d(kernel_size=2, stride=2)
        )
        
        self.fc = nn.Sequential(
            # 全连接层1
            nn.Linear(in_features=16 * 5 * 5, out_features=120), 
            nn.ReLU(),
            # 全连接层2
            nn.Linear(in_features=120, out_features=84), 
            nn.ReLU(),
            nn.Linear(in_features=84, out_features=10)
        )
    def forward(self, img):
        img = self.conv(img)
        out = img.view(img.size(0),-1)
        out = self.fc(out)
        return out

summary(net, (1, 28, 28))

----------------------------------------------------------------
     Layer (type)               Output Shape         Param #
================================================================
         Conv2d-1            [-1, 6, 28, 28]             156
           ReLU-2            [-1, 6, 28, 28]               0
      MaxPool2d-3            [-1, 6, 14, 14]               0
         Conv2d-4           [-1, 16, 10, 10]           2,416
           ReLU-5           [-1, 16, 10, 10]               0
      MaxPool2d-6             [-1, 16, 5, 5]               0
         Linear-7                  [-1, 120]          48,120
           ReLU-8                  [-1, 120]               0
         Linear-9                   [-1, 84]          10,164
          ReLU-10                   [-1, 84]               0
        Linear-11                   [-1, 10]             850
================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
----------------------------------------------------------------

LetNet 训练

超参数的设置

首先我们进行超参数的设置

lr = 1e-2
momentum = 0.9
weight_decay = 5e-4
nepochs = 300
optimizer = optim.SGD(net.parameters(), lr=lr, momentum=momentum, weight_decay=weight_decay, nesterov=True) # 优化器
criterion = nn.CrossEntropyLoss()
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', factor=0.5,verbose=True,patience = 5,min_lr = 0.000001) # 动态更新学习率

训练及测试模型

然后我们就可以进行训练了

[150/200, 9 seconds]|	 loss: 0.27686, accuaracy: 99.99%	|	val_loss: 3.08028, val_accuaracy: 99.08%
[151/200, 9 seconds]|	 loss: 0.27358, accuaracy: 99.98%	|	val_loss: 3.05407, val_accuaracy: 98.99%
[152/200, 9 seconds]|	 loss: 0.27556, accuaracy: 99.99%	|	val_loss: 3.21076, val_accuaracy: 98.99%
[153/200, 9 seconds]|	 loss: 0.27647, accuaracy: 99.98%	|	val_loss: 3.00075, val_accuaracy: 99.08%
[154/200, 9 seconds]|	 loss: 0.27396, accuaracy: 99.98%	|	val_loss: 3.15662, val_accuaracy: 99.03%
[155/200, 8 seconds]|	 loss: 0.27436, accuaracy: 99.98%	|	val_loss: 2.98197, val_accuaracy: 99.05%
[156/200, 9 seconds]|	 loss: 0.27354, accuaracy: 99.98%	|	val_loss: 3.07788, val_accuaracy: 99.07%
[157/200, 9 seconds]|	 loss: 0.27384, accuaracy: 99.98%	|	val_loss: 3.07084, val_accuaracy: 99.07%
[158/200, 9 seconds]|	 loss: 0.27617, accuaracy: 99.98%	|	val_loss: 2.97456, val_accuaracy: 99.04%
[159/200, 9 seconds]|	 loss: 0.27438, accuaracy: 99.98%	|	val_loss: 3.24354, val_accuaracy: 99.03%
[160/200, 9 seconds]|	 loss: 0.27527, accuaracy: 99.99%	|	val_loss: 2.94451, val_accuaracy: 99.06%
[161/200, 9 seconds]|	 loss: 0.27702, accuaracy: 99.98%	|	val_loss: 2.98104, val_accuaracy: 99.07%
Epoch   162: reducing learning rate of group 0 to 2.5000e-04.
[162/200, 9 seconds]|	 loss: 0.27402, accuaracy: 99.99%	|	val_loss: 2.98107, val_accuaracy: 99.03%
[163/200, 9 seconds]|	 loss: 0.25684, accuaracy: 99.99%	|	val_loss: 2.99173, val_accuaracy: 99.03%
[164/200, 9 seconds]|	 loss: 0.25519, accuaracy: 99.99%	|	val_loss: 2.97158, val_accuaracy: 99.05%
[165/200, 9 seconds]|	 loss: 0.25442, accuaracy: 99.99%	|	val_loss: 3.02820, val_accuaracy: 99.03%
[166/200, 9 seconds]|	 loss: 0.25639, accuaracy: 99.99%	|	val_loss: 3.00219, val_accuaracy: 99.02%
[167/200, 14 seconds]|	 loss: 0.25652, accuaracy: 99.99%	|	val_loss: 2.99334, val_accuaracy: 99.04%
[168/200, 20 seconds]|	 loss: 0.25747, accuaracy: 99.99%	|	val_loss: 2.99055, val_accuaracy: 99.03%
[169/200, 20 seconds]|	 loss: 0.25656, accuaracy: 99.99%	|	val_loss: 3.06458, val_accuaracy: 99.00%
[170/200, 20 seconds]|	 loss: 0.25671, accuaracy: 99.99%	|	val_loss: 2.98292, val_accuaracy: 99.06%
Epoch   171: reducing learning rate of group 0 to 1.2500e-04.
[171/200, 20 seconds]|	 loss: 0.25611, accuaracy: 99.99%	|	val_loss: 3.05042, val_accuaracy: 99.04%
[172/200, 19 seconds]|	 loss: 0.24839, accuaracy: 99.99%	|	val_loss: 2.99352, val_accuaracy: 99.05%
[173/200, 20 seconds]|	 loss: 0.24867, accuaracy: 99.99%	|	val_loss: 3.02229, val_accuaracy: 99.04%
[174/200, 19 seconds]|	 loss: 0.24922, accuaracy: 99.99%	|	val_loss: 3.16668, val_accuaracy: 99.02%
[175/200, 20 seconds]|	 loss: 0.24915, accuaracy: 99.99%	|	val_loss: 2.99517, val_accuaracy: 99.06%
[176/200, 19 seconds]|	 loss: 0.24904, accuaracy: 99.99%	|	val_loss: 3.00806, val_accuaracy: 99.09%
[177/200, 20 seconds]|	 loss: 0.24985, accuaracy: 99.99%	|	val_loss: 2.97943, val_accuaracy: 99.04%
Epoch   178: reducing learning rate of group 0 to 6.2500e-05.
[178/200, 20 seconds]|	 loss: 0.24854, accuaracy: 100.00%	|	val_loss: 3.00098, val_accuaracy: 99.05%
[179/200, 22 seconds]|	 loss: 0.24590, accuaracy: 99.99%	|	val_loss: 3.18777, val_accuaracy: 99.01%
[180/200, 21 seconds]|	 loss: 0.24560, accuaracy: 99.99%	|	val_loss: 2.98851, val_accuaracy: 99.04%
[181/200, 20 seconds]|	 loss: 0.24541, accuaracy: 99.99%	|	val_loss: 2.97614, val_accuaracy: 99.05%
[182/200, 20 seconds]|	 loss: 0.24442, accuaracy: 99.99%	|	val_loss: 3.00202, val_accuaracy: 99.05%
[183/200, 19 seconds]|	 loss: 0.24540, accuaracy: 99.99%	|	val_loss: 2.99175, val_accuaracy: 99.04%
[184/200, 20 seconds]|	 loss: 0.24519, accuaracy: 99.99%	|	val_loss: 2.97485, val_accuaracy: 99.04%
[185/200, 20 seconds]|	 loss: 0.24594, accuaracy: 99.99%	|	val_loss: 3.20352, val_accuaracy: 99.01%
[186/200, 19 seconds]|	 loss: 0.24565, accuaracy: 99.99%	|	val_loss: 2.99283, val_accuaracy: 99.05%
[187/200, 20 seconds]|	 loss: 0.24578, accuaracy: 99.99%	|	val_loss: 2.99267, val_accuaracy: 99.03%
Epoch   188: reducing learning rate of group 0 to 3.1250e-05.
[188/200, 20 seconds]|	 loss: 0.24562, accuaracy: 99.99%	|	val_loss: 2.99241, val_accuaracy: 99.04%
[189/200, 20 seconds]|	 loss: 0.24353, accuaracy: 99.99%	|	val_loss: 3.06091, val_accuaracy: 98.99%
[190/200, 19 seconds]|	 loss: 0.24347, accuaracy: 99.99%	|	val_loss: 2.98877, val_accuaracy: 99.05%
[191/200, 20 seconds]|	 loss: 0.24334, accuaracy: 99.99%	|	val_loss: 2.98441, val_accuaracy: 99.06%
[192/200, 20 seconds]|	 loss: 0.24403, accuaracy: 99.99%	|	val_loss: 2.98862, val_accuaracy: 99.04%
[193/200, 20 seconds]|	 loss: 0.24362, accuaracy: 99.99%	|	val_loss: 2.99172, val_accuaracy: 99.04%
[194/200, 20 seconds]|	 loss: 0.24385, accuaracy: 99.99%	|	val_loss: 2.98552, val_accuaracy: 99.03%
[195/200, 19 seconds]|	 loss: 0.24354, accuaracy: 99.99%	|	val_loss: 3.02285, val_accuaracy: 99.01%
[196/200, 19 seconds]|	 loss: 0.24350, accuaracy: 99.99%	|	val_loss: 2.98058, val_accuaracy: 99.06%
Epoch   197: reducing learning rate of group 0 to 1.5625e-05.
[197/200, 20 seconds]|	 loss: 0.24376, accuaracy: 99.99%	|	val_loss: 2.98606, val_accuaracy: 99.05%
[198/200, 20 seconds]|	 loss: 0.24254, accuaracy: 99.99%	|	val_loss: 2.99047, val_accuaracy: 99.04%
[199/200, 21 seconds]|	 loss: 0.24260, accuaracy: 99.99%	|	val_loss: 2.98837, val_accuaracy: 99.04%
[200/200, 13 seconds]|	 loss: 0.24253, accuaracy: 99.99%	|	val_loss: 2.98588, val_accuaracy: 99.04%

我们可以看到，最后迭代200次之后，我们的准确率大概有99.04%

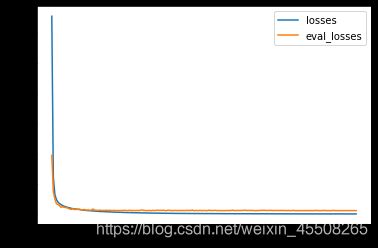
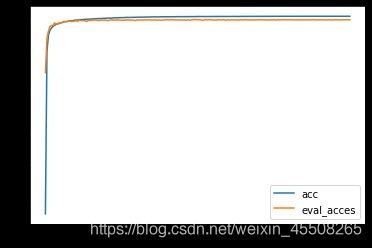
可视化误差曲线，准确率曲线

可以看出来，我们的误差逐渐减小，但是到达一定的次数之后，误差减小的越来越慢

准确率也是逐渐增大，然后到达一定程度变化很小

结果可视化，查看每一类的准确率

dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images[:4]
labels = labels[:4]
# print images
plot_img(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))


outputs = net(images.to(device))
_, predicted = torch.max(outputs.cpu(), 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(4)))

correct = 0
total = 0
with torch.no_grad():
    for data in test_loader:
        images, labels = data
        images, labels = images.to(device), labels.to(device)
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %.2f %%' % 
      (100 * correct / total))

class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in test_loader:
        images, labels = data
        images, labels = images.to(device), labels.to(device)
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(len(labels)):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1


for i in range(10):
    print('Accuracy of %5s : %2.2f %%' % (classes[i], 100 * class_correct[i] / class_total[i]))

GroundTruth:      5     3     5     2
Predicted:      5     3     5     2
Accuracy of the network on the 10000 test images: 99.04 %
Accuracy of     0 : 99.49 %
Accuracy of     1 : 99.56 %
Accuracy of     2 : 99.32 %
Accuracy of     3 : 99.31 %
Accuracy of     4 : 99.08 %
Accuracy of     5 : 98.54 %
Accuracy of     6 : 98.64 %
Accuracy of     7 : 98.93 %
Accuracy of     8 : 98.97 %
Accuracy of     9 : 98.41 %

模型的保存与加载

PATH = './mnist_net.pth'
torch.save(net, PATH) # 保存模型

net2 = torch.load(PATH) # 加载模型

步骤2：生成针对该网络的对抗样本。

威胁模型

在深度学习中，有许多类型的对抗性攻击，每一类攻击都有不同的目标和对攻击者知识的假设。然而，总的目标是在输入数据中添加最少的扰动，以导致所需的错误分类。攻击者的知识有几种假设，其中两种是:白盒和黑盒。白盒攻击假定攻击者具有对模型的全部知识和访问权，包括体系结构、输入、输出和权重。黑盒攻击假设攻击者只访问模型的输入和输出，对底层架构或权重一无所知。目标也有几种类型，包括错误分类和源/目标错误分类。错误分类的目标意味着对手只希望输出分类是错误的，而不关心新的分类是什么。源/目标错误分类意味着对手想要更改原来属于特定源类的图像，以便将其分类为特定的目标类。

在这种情况下，FGSM攻击是一种以错误分类为目标的白盒攻击。

快速梯度符号攻击

到目前为止，最早也是最流行的对抗性攻击之一被称为快速梯度符号攻击(FGSM)，由Goodfellow等人在解释和利用对抗性示例( Explaining and Harnessing Adversarial Examples)时介绍到。这种攻击非常强大，而且直观。它被设计用来攻击神经网络，利用他们学习的方式，梯度gradients。这个想法很简单，比起根据后向传播梯度来调整权重使损失最小化，这种攻击是根据相同的反向传播梯度调整输入数据来最大化损失。换句话说，攻击使用了输入数据相关的梯度损失方式，通过调整输入数据，使损失最大化。

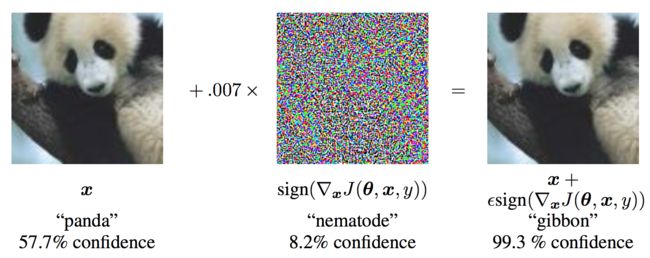
在我们深入代码之前，让我们看看著名的FGSM panda示例并提取一些符号。

从图像中看，$\mathbf{x}$ 是一个正确分类为“熊猫”(panda)的原始输入图像， y 是对 $\mathbf{x}$ 的真实表征标签ground truth label, $\theta$ 表示模型参数， 而 $J(\theta ,\mathbf{x},y)$ 是用来训练网络的损失函数。 这种攻击将梯度后向传播到输入数据来计算${\nabla }_{x}J(\theta ,\mathbf{x},y)$。然后将输入数据通过一小步 $ϵ$ 或 如图中的0.007 ) 在(i.e. $sign({\nabla }_{x}J(\theta ,\mathbf{x},y))$ 方向上调整，使损失最大化。结果将得到受到干扰的图像， x′，尽管图片还是“熊猫”，但它一杯目标网络错误分类为“长臂猿”(gibbon)了

定义扰动上限 epsilons

我们的需要定义我们的epsilons : 要用于运行的epsilon值的列表。在列表中保留0是很重要的，因为它代表了原始测试集上的模型性能。而且，直觉上我们认为，epsilon越大，扰动越明显，但在降低模型精度方面攻击越有效。因为这里的数据范围是 [0,1]，所以取值不应该超过1。

我们还定义了我们的预训练的模型，也就是我们的LetNet模型

除此之外，还有一个use_cuda : 如果需要和可用，使用CUDA的布尔标志。其实也就是方便我们的用GPU和CPU的区别

epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "./mnist_net.pth"
use_cuda=True

被攻击的模型

我们的被攻击的模型就是我们刚刚用的LetNet模型，所以我们需要定义模型和数据加载器，然后初始化模型并加载预训练的权重。

# 定义我们正在使用的设备
print("CUDA Available: ",torch.cuda.is_available())
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")

model = torch.load(pretrained_model)
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")
model = net.to(device)
model

CUDA Available:  True
LeNet(
(conv): Sequential(
 (0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
 (1): ReLU()
 (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
 (3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
 (4): ReLU()
 (5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(fc): Sequential(
 (0): Linear(in_features=400, out_features=120, bias=True)
 (1): ReLU()
 (2): Linear(in_features=120, out_features=84, bias=True)
 (3): ReLU()
 (4): Linear(in_features=84, out_features=10, bias=True)
)
)

FGSM 攻击方式

现在，我们可以定义一个通过打乱原始输入来生成对抗性示例的函数。 fgsm_attack 函数有3个输入, image 是原始图像 x ， epsilon 是像素级干扰量 $ϵ$，data_grad 是关于输入图像 ${\nabla }_{x}J(\theta ,\mathbf{x},y)$ 的损失。然后该函数创建干扰图像如下
$$perturbed\_image=image+epsilon\ast sign(data\_grad)=x+ϵ\ast sign({\nabla }_{x}J(\theta ,\mathbf{x},y))$$
最后，为了保持数据的原始范围，将扰动后的图像截取范围在 [0,1]。

# FGSM算法攻击代码
def fgsm_attack(image, epsilon, data_grad):
    # 收集数据梯度的元素符号
    sign_data_grad = data_grad.sign()
    # 通过调整输入图像的每个像素来创建扰动图像
    perturbed_image = image + epsilon*sign_data_grad
    # 添加剪切以维持[0,1]范围
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # 返回被扰动的图像
    return perturbed_image

测试函数

首先，我们需要定义一个测试函数。每次调用此测试函数都会对 MNIST 测试集执行完整的测试步骤，并报告最终的准确性。但是，请注意， 此函数也需要输入epsilon。这是因为test函数展示受到强度为$ϵ$的攻击下被攻击模型的准确性。 更具体地说，对于测试集中的每个样本，该函数计算输入数据data_grad的损失梯度，用fgsm_attack（perturbed_data） 创建扰乱图像，然后检查扰动的例子是否是对抗性的。除了测试模型的准确性之外，该函数还保存并返回一些成功的对抗性示例，以便稍后可视化。

def test(model, device, test_loader, epsilon):

    # 精度计数器
    correct = 0
    adv_examples = []

    # 循环遍历测试集中的所有示例
    for data, target in test_loader:
        # 把数据和标签发送到设备
        data, target = data.to(device), target.to(device)

        # 设置张量的requires_grad属性，这对于攻击很关键
        data.requires_grad = True

        # 通过模型前向传递数据
        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability

        # 如果初始预测是错误的，不打断攻击，继续
        if init_pred.item() != target.item():
            continue

        # 计算损失
        loss = F.nll_loss(output, target)

        # 将所有现有的渐变归零
        model.zero_grad()
        # 计算后向传递模型的梯度
        loss.backward()

        # 收集datagrad
        data_grad = data.grad.data
        # 唤醒FGSM进行攻击
        perturbed_data = fgsm_attack(data, epsilon, data_grad)
        # 重新分类受扰乱的图像
        output = model(perturbed_data)
        
        # 检查是否成功
        final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
        if final_pred.item() == target.item():
            correct += 1
            # 保存0 epsilon示例的特例
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
        else:
            # 稍后保存一些用于可视化的示例
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )

    # 计算这个epsilon的最终准确度
    final_acc = correct/float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    # 返回准确性和对抗性示例
    return final_acc, adv_examples

启动攻击

实现的最后一部分是运行攻击操作。在这里，我们对输入中的每个epsilon值运行一个完整的测试步骤。对于每个epsilon，我们也保存最后的精度和一些将在接下来的部分中绘制的成功的对抗性例子。请注意，随着epsilon值的增加，打印出来的精度是如何降低的。另外，注意$ϵ=0$用例表示原始未受攻击的测试准确性。

accuracies = []
examples = []

# 对每个epsilon运行测试
for eps in epsilons:
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

Epsilon: 0	Test Accuracy = 9904 / 10000 = 0.9904
Epsilon: 0.05	Test Accuracy = 9690 / 10000 = 0.969
Epsilon: 0.1	Test Accuracy = 9079 / 10000 = 0.9079
Epsilon: 0.15	Test Accuracy = 7557 / 10000 = 0.7557
Epsilon: 0.2	Test Accuracy = 5029 / 10000 = 0.5029
Epsilon: 0.25	Test Accuracy = 3029 / 10000 = 0.3029
Epsilon: 0.3	Test Accuracy = 1596 / 10000 = 0.1596

对抗结果

准确性 vs Epsilon

第一个结果是精度与 epsilon 图。如前所述，随着 epsilon 的增加，我们期望测试精度降低。这是因为较大的 epsilons 意味着我们朝着最 大化损失的方向迈出更大的一步。请注意，即使 epsilon 值线性分布，曲线中的趋势也不是线性的。例如，ε= 0.05 时的精度仅比 ε= 0 低 约 2％，但ε= 0.2 时的精度比 ε= 0.15 低 25％。另外，请注意在 ε= 0.25 和 ε= 0.3 之间模型的准确性达到10级分类器的随机精度。

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

样本对抗性示例

正如天底下没有免费午餐。在这种情况下，随着 epsilon 增加，测试精度降低，但同时扰动也在变得更容易察觉。实际上，在攻击者必须考虑权衡准确度降级和可感知性。在这里，我们展示了每个 epsilon 值的成功对抗性示例的一些例子。图的每一行显示不同的 epsilon 值。第一行是 ε= 0 的例子，它们代表没有扰动的原始“干净”图像。每个图像的标题显示“原始分类 - >对抗性分类。”注意，扰动在 ε= 0.15 时开始 变得明显，并且在 ε= 0.3 时非常明显。然而，在所有情况下，尽管增加了噪音，人类仍然能够识别正确的类别。

# 在每个epsilon上绘制几个对抗样本的例子
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

总结

希望这能够提供一些关于你对抗性机器学习主题的见解。从这里开始有很多可能的方向。这种攻击代表了对抗性攻击研究的开始，并且自从有了许多关于如何攻击和保护ML模型不受对手攻击的后续想法以来。事实上，在NIPS 2017年有一场对抗性的攻防竞赛，本文描述了很多比赛中使用的方法:对抗性的攻防及竞赛(Adversarial Attacks and Defences Competition）。在防御方面的工作也引入了使机器学习模型在一般情况下更健壮robust的想法，这是一种自然扰动和反向精心设计的输入。

另一个研究方向是不同领域的对抗性攻击和防御。对抗性研究并不局限于图像领域，就比如这种语音到文本模型speech-to-text models的攻击。当然，了解更多关于对抗性机器学习的最好方法是多动手。首先，尝试实现一个不同于NIPS 2017比赛的攻击，看看它与FGSM有什么不同，然后，尝试设计保护模型，使其免于自己的攻击。

利用GAN，我们可以见到不一样的风景，这也有可能，眼见不一定为实，耳听也不一定是真的，很有可能都是我们通过GAN生成出来的。有可能我们看到的是一个虚拟现实了，不过还是很喜欢GAN，也相信未来他一定会大放光彩。

参考

• ADVERSARIAL EXAMPLE GENERATION
• Generative adversarial network - Wikipedia
• TORCH.OPTIM
• LeNet-5实现MNIST分类
• 详解卷积神经网络(CNN)