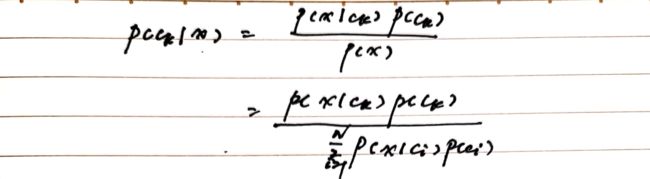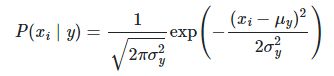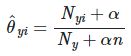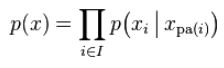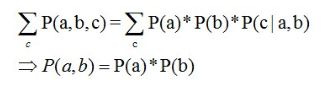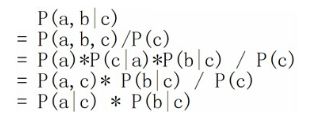基于朴素贝叶斯分类器的西瓜数据集 2.0 预测分类_八哥的机器学习深化笔记12_朴素贝叶斯...
判别模型：学习得到条件概率分布P(y|x)，即在特征x出现的情况下标记y出现的概率。典型的判别模型包括：KNN、感知机、决策树、线性回归、逻辑斯蒂回归模型、支持向量机、神经网络、boosting提升方法。
生成模型：学习得到联合概率分布P(x,y)，即特征x和标记y共同出现的概率，然后求条件概率分布。能够学习到数据生成的机制。
之所以称为生成方法，是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有：朴素贝叶斯法、隐马尔科夫模型、高斯混合模型。
朴素贝叶斯最广的应用是在文档分类、垃圾文本过滤(如垃圾邮件、垃圾信息等)、情感分析(微博、论坛上的积极、消极等情绪判别)这些方面，除此之外还有多分类实时预测、推荐系统(贝叶斯与协同过滤组合使用)、拼写矫正(当你输入一个错误单词时，可以通过文档库中出现的概率对你的输入进行矫正)等。贝叶斯推理提供了推理的一种概率手段，它为直接运用概率的学习算法提供了理论框架。
贝叶斯公式
贝叶斯分类器
朴素贝叶斯分类器
参数估计
优缺点
贝叶斯网络
1.贝叶斯公式
·先验概率，就是根据以往的经验或者现有数据的分析所得到的概率。如，随机扔一枚硬币，则p(正面) = p(反面) = 1/2，这是我们根据已知的知识所知道的信息，即p(正面) = 1/2为先验概率。
·条件概率是指事件B在另一事件A发生的条件下发送的概率。用数学符号表示为：P(B|A)，即B在A发生的条件下发生的概率。类似然同此意。举个栗子，你早上误喝了一瓶过期了的牛奶(A)，那我们来算一下你今天拉肚子的概率(B)，这个就叫做条件概率。即P(拉肚子|喝了过期牛奶)，易见，条件概率是由因求果(知道原因推测结果)。
·后验概率跟条件概率的表达形式有点相似。数学表达式为p(A|B), 即A在B发生的条件下发生的概率。以误喝牛奶的例子为例，现在知道了你今天拉肚子了(B)，算一下你早上误喝了一瓶过期了的牛奶(A)的概率, 即P(A|B)，这就是后验概率，后验概率是由果求因(知道结果推出原因)。
2.贝叶斯分类器
假设分类问题有N种类别c1，c2，...，cN，对于一个实例x进行分类时，贝叶斯分类器先根据贝叶斯公式分别计算在x条件下属于各个类别的条件概率，即：
然后根据后验概率最大化原则，将x归为有最大后验概率的类别。
贝叶斯分类器的假设函数可定义为(y是分类问题的类别集)：
argmax函数求出使
最大的x值。
因为各后验概率的分母都是全概率，相同，所以假设函数可以是：
tips：上述P(ck)为样本类别ck出现的频率，即样本类别ck出现的次数mk除以样本总数m。
3.朴素贝叶斯分类器
朴素贝叶斯是在贝叶斯的基础上进行了相应的简化，是贝叶斯分类器中的一种，也是最简单，最常用的分类器。它有一个很强悍的假设条件——“特征(属性)条件独立性假设”，即假设x的各个特征之间相互独立，一个特征出现的概率不受其他特征的影响。也即是朴素的原因：假设属性是相互独立的。如果属性之间存在关联，分类准确率会降低。但在大部分情况下，朴素贝叶斯的分类效果都不错。
朴素贝叶斯分类的核心思想是找出后验概率最大的那个类，而不是求出其精确的概率。
如果属性之间的相互依赖对所有类别的影响相同，或者相互依赖关系可以互相抵消，那么属性条件独立性的假设在降低计算开销的同时不会对分类结果产生不良影响。
朴素贝叶斯是没有超参数可以调的，所以它不需要调参，朴素贝叶斯是根据训练集进行分类，分类出来的结果基本上就是确定了的。
朴素贝叶斯对异常值不敏感。所以在进行数据处理时，我们可以不去除异常值，因为保留异常值可以保持朴素贝叶斯算法的整体精度，而去除异常值则可能在进行预测的过程中由于失去部分异常值导致模型的泛化能力下降。
朴素贝叶斯是低方差模型。(误差 = 偏差 + 方差)对于复杂模型来说，由于复杂模型充分拟合了部分数据，使得它们的偏差变小，但由于对部分数据过分拟合，这就导致预测的方差会变大。因为朴素贝叶斯假设了各个属性之间是相互的，算是一个简单的模型。对于简单的模型来说，则恰恰相反，简单模型的偏差会更大，相对的，方差就会较小。(偏差是模型输出值与真实值的误差，也就是模型的精准度，方差是预测值与模型输出期望的的误差，即模型的稳定性，也就是数据的集中性的一个指标)
4.参数估计
4.1极大似然估计
朴素贝叶斯分类器的假设函数确定后，接下来需要根据训练样本对模型参数使用极大似然法进行估计。模型参数包括所有的先验概率P(ck)以及所有的类似然P(x(j)|ck)。
常用的朴素贝叶斯分类器分为伯努利模型、多项式模型、高斯模型等。
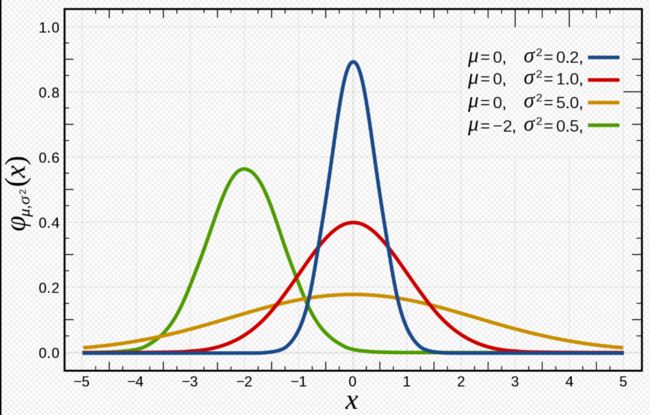
高斯朴素贝叶斯：特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。高斯分布又叫正态分布，我们把一个随机变量 X服从数学期望为μ，方差为σ^2 的数据分布称为正态分布，当μ=0，σ=1是称为标准 正态分布(对应红色的线)
多项式朴素贝叶斯：特征变量是离散变量，符合多项分布，计算数据的条件概率(使用拉普拉斯平滑法(后面会讲)处理的一个模型)，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。注意，多项式朴素贝叶斯实际上符合多项式分布，不会存在负数，所以传入输入的时候，别用StandardScaler进行归一化数据，可以使用MinMaxScaler进行归一化。
伯努利朴素贝叶斯：特征变量是布尔变量，符合伯努利分布，在文档分类中特征是单词是否出现。伯努利分布就是我们常见的0-1分布，即它的随机变量只取0或者1，各自的频率分别取1-p和p，当x=0或者x-1时，我们数学定义为：
伯努利朴素贝叶斯模型是基于以下公式：
为了使推导过程容易理解，我们以简单的伯努利模型来演示使用极大似然法估计模型参数的过程。伯努利模型可以进行多元分类，即P(ck)服从多项式分布，但为了推导简单，这里仅做二元分类，即P(ck)服从伯努利分布。
再根据样本独立同分布以及特征条件独立性假设，可得：
4.2贝叶斯估计
使用极大似然估计可能会出现所估计的概率为0的情况，这会影响后验概率的计算结果，导致分类产生偏差，采用贝叶斯估计可以解决这个问题。
我们发现，使用贝叶斯估计得到的概率都是大于0的，并且λ任意取大于等于0的常数都不会破坏概率之和为1的概率律。
tips：
拉普拉斯平滑法是朴素贝叶斯中处理零概率问题的一种修正方式。在进行分类的时候，可能会出现某个属性在训练集中没有与某个类同时出现过的情况，如果直接基于朴素贝叶斯分类器的表达式进行计算的话就会出现零概率现象。为了避免其他属性所携带的信息被训练集中未出现过的属性值“抹去”，所以才使用拉普拉斯估计器进行修正。具体的方法是：
在分子上加1；
对于先验概率，在分母上加上训练集中可能的类别数；对于条件概率，则在分母上加上第i个属性可能的取值数。
5.优缺点
朴素贝叶斯的主要优点有：
1)朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
2)对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练(朴素贝叶斯在训练过程中只需要计算各个类的概率和各个属性的类条件概率，这些概率值可以快速地根据增量数据进行更新，无需重新全量计算)。
3)对缺失数据不太敏感，算法也比较简单，常用于文本分类。
4)分类准确度高，速度快。
朴素贝叶斯的主要缺点有：
1) 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2)需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3)由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
4)对输入数据的表达形式很敏感。
6.贝叶斯网络
6.1贝叶斯网络的定义
贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。
贝叶斯网络的有向无环图中的节点表示随机变量
，它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。
例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：
简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。
令G = (L,E)表示一个有向无环图(DAG)，其中 L 代表图形中所有的节点的集合，而 E 代表有向连接线段的集合，且令X = (Xi) i ∈ L为其有向无环图中的某一节点 i 所代表的随机变量，若节点 X 的联合概率可以表示成：
则称X为相对于一有向无环图G 的贝叶斯网络，其中，
表示节点 i 之“因”，或称 pa(i) 是 i 的parents(父母)。
此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：
如下图所示，便是一个简单的贝叶斯网络：
因为a导致b，a和b导致c，所以有:
6.2贝叶斯网络的3种结构形式
给定如下图所示的一个贝叶斯网络：
从图上可以比较直观的看出：
(1). x1,x2,…x7的联合分布为:
(2). x1和x2独立(对应head-to-head)；
(3). x6和x7在x4给定的条件下独立(对应tail-to-tail)。
根据上图，第1点可能很容易理解，但第2、3点中所述的条件独立是啥意思呢？其实第2、3点是贝叶斯网络中3种结构形式中的其中二种。为了说清楚这个问题，需要引入D-Separation(D-分离)这个概念。
D-Separation是一种用来判断变量是否条件独立的图形化方法。换言之，对于一个DAG(有向无环图)E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。
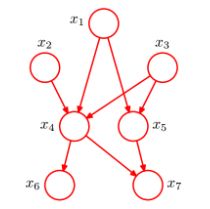
6.2.1形式1：head-to-head
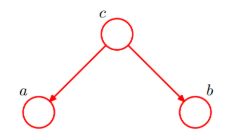
贝叶斯网络的第一种结构形式如下图所示：
所以有：P(a,b,c) = P(a)*P(b)*P(c|a,b)成立，化简后可得：
即在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立，对应本节中最开始那张图中的“x1、x2独立”。
tips：这里a，b均为已知，不然没法求，且P(a,b,c)=P(a,b)*P(c|a,b)。
6.2.2形式2：tail-to-tail
贝叶斯网络的第二种结构形式如下图所示:
考虑c未知，跟c已知这两种情况：
在c未知的时候，有：P(a,b,c)=P(c)*P(a|c)*P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
在c已知的时候，有：P(a,b|c)=P(a,b,c)/P(c)，然后将
P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知时，a、b独立。
所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为tail-to-tail条件独立，对应本节中最开始那张图中的“x6和x7在x4给定的条件下独立”。
6.2.3形式3：head-to-tail
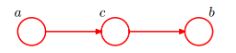
贝叶斯网络的第三种结构形式如下图所示：
还是分c未知跟c已知这两种情况：
c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。
c已知时，有：P(a,b|c)=P(a,b,c)/P(c)，且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c)，可化简得到：
所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。
插一句：这个head-to-tail其实就是一个链式网络，如下图所示：
根据之前对head-to-tail的讲解，我们已经知道，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢？意味着：xi+1的分布状态只和xi有关，和其他变量条件独立。通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链(Markov chain)。且有：
参考资料：
Python机器学习算法 原理、实现与案例——刘硕
【白话机器学习】算法理论+实战之朴素贝叶斯
https://mp.weixin.qq.com/s/IXpv5QSoHM8Bx4ZQgYbm3g
伯努利分布、二项分布、几何分布、超几何分布、泊松分布
https://blog.csdn.net/solo_sky/article/details/47777943
大话系列 | 贝叶斯(下)—实战项目
https://mp.weixin.qq.com/s/rTO1di0NV4o8b4s5Gr3R_Q
【机器学习】朴素贝叶斯算法(Naive Bayes，NB)
https://mp.weixin.qq.com/s/fAnHcCVwm5d7RqZqT1uKYQ
朴素贝叶斯算法原理小结
https://www.cnblogs.com/pinard/p/6069267.html
https://posts.careerengine.us/p/5d5aa26e1590f00bc24b9384
生成模型 VS 判别模型 (含义、区别、对应经典算法)
https://blog.csdn.net/u010358304/article/details/79748153
生成模型，判别模型，以及朴素贝叶斯
https://blog.csdn.net/G090909/article/details/50209189
超详细讲解贝叶斯网络(Bayesian network)
https://www.cnblogs.com/USTC-ZCC/p/12786860.html
从贝叶斯方法谈到贝叶斯网络
https://blog.csdn.net/v_JULY_v/article/details/40984699