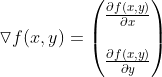机器学习-逻辑回归（Logistic regression）

我们日常生活中遇到过很多最优化问题，比如如何再最短时间内从A点到达B点？如何投入最少工作量缺获得最大的效益？如何设计发动机使得油耗最少而功率最大？可见，最优化的作用十分强大。

目录

什么是Logistic回归

基于Logistic回归和Sigmoid函数的分类 

基于最优化方法的最佳回归系数确定

梯度上升法

梯度上升算法实现

画出决策边界

完整代码

总结

---

什么是Logistic回归

什么是回归？假设现在有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。

Logistic回归（logistic regression）是统计学习中的经典分类方法，实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，有的教材也称Logistic回归为对数几率回归。这里要注意，虽然带有回归的字眼，但是该模型是一种分类算法，Logistic回归是一种线性分类器，针对的是线性可分问题。利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。

基于Logistic回归和Sigmoid函数的分类 

我们理想的函数是能接受所有的输入然后预测出类别。例如，在两个类的情况下，输出0或1。或许你之前接触过具有这种性质的函数，该函数称为海维赛德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。然而其问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。而Sigmoid函数也有类似的性质并且数学上更容易处理。Sigmoid函数具体的计算公式如下：

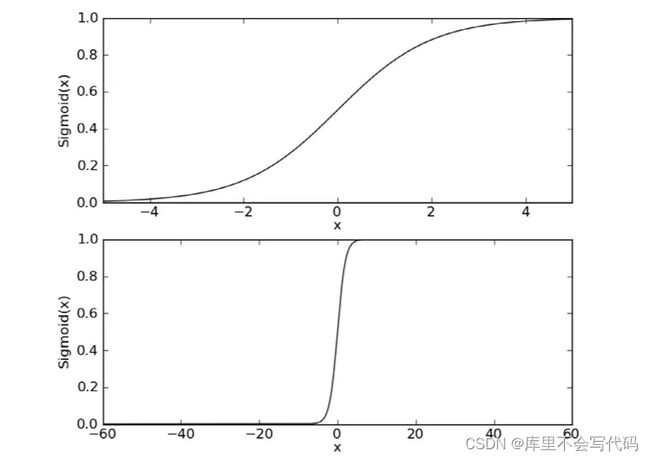
下图给出了Sigmoid函数在不同坐标尺度下的两条曲线图。

两种坐标尺度下的Sigmoid函数图。上图的横坐标范围是（-5,5），这时的曲线变化较为平滑；下图横坐标的尺度足够大，可以看到，在x=0点处Sigmoid函数看起来很像阶跃函数。

因此，为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在（0,1）之间的数值。任何大于0.5的数据被分入1类，小于0.5的数据被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

确定了分类器的函数形式之后，现在的问题变成了：最佳回归系数是多少？如何确定它们的大小？

基于最优化方法的最佳回归系数确定

梯度上升法

梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。

如果梯度记为▽，则函数f(x,y)的梯度由下式表示：

这个梯度意味着要沿x的方向移动 ，沿y的方向移动。

普通梯度上升算法实现

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
    labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
    m, n = np.shape(dataMatrix)   #返回dataMatrix的大小。m为行数,n为列数。
    alpha = 0.01   #移动步长,也就是学习速率,控制更新的幅度。
    maxCycles = 500   #最大迭代次数
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)  #梯度上升矢量化公式
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights.getA(),weights_array #将矩阵转换为数组，返回权重数组

随机梯度上升算法实现

        普通梯度上升算法在每次更新回归数据时都需要遍历整个数据集，该方法处理100个左右的数据集尚可，但如果有数十亿的样本和成千上万的特征，那么该方法的复杂度就太高了。因此就引入了随机梯度算法。相较于普通的梯度上升算法来说，随机梯度算法一次仅用一个样本点来更新回归系数。

def gradAscent(dataMatIn, classLabels):
	dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
	labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
	m, n = np.shape(dataMatrix)	#返回dataMatrix的大小。m为行数,n为列数。
	alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
	maxCycles = 500	#最大迭代次数
	weights = np.ones((n,1))
	for k in range(maxCycles):
		h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
		error = labelMat - h
		weights = weights + alpha * dataMatrix.transpose() * error
	return weights.getA() #将矩阵转换为数组，返回权重数组

alpha在每次迭代的时候都会调整，并且，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为这里还存在一个常数项。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果需要处理的问题是动态变化的，那么可以适当加大上述常数项，来确保新的值获得更大的回归系数。另一点值得注意的是，在降低alpha的函数中，alpha每次减少1/(j+i)，其中j是迭代次数，i是样本点的下标。第二个改进的地方在于跟新回归系数(最优参数)时，只使用一个样本点，并且选择的样本点是随机的，每次迭代不使用已经用过的样本点。这样的方法，就有效地减少了计算量，并保证了回归效果。

画出决策边界

完整代码

import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:梯度上升算法测试函数
求函数f(x) = -x^2 + 4x的极大值
"""
def Gradient_Ascent_test():
	def f_prime(x_old):	#f(x)的导数
		return -2 * x_old + 4
	x_old = -1	#初始值，给一个小于x_new的值
	x_new = 0	#梯度上升算法初始值，即从(0,0)开始
	alpha = 0.01#步长，也就是学习速率，控制更新的幅度
	presision = 0.00000001	#精度，也就是更新阈值
	while abs(x_new - x_old) > presision:
		x_old = x_new
		x_new = x_old + alpha * f_prime(x_old)#上面提到的公式
	print(x_new)#打印最终求解的极值近似值
"""
函数说明:加载数据
"""
def loadDataSet():
	dataMat = []	#创建数据列表
	labelMat = []	#创建标签列表
	fr = open('testSet.txt')#打开文件	
	for line in fr.readlines():	#逐行读取
		lineArr = line.strip().split()列表
		dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#添加数据
		labelMat.append(int(lineArr[2]))
	fr.close()
	return dataMat, labelMat
"""
函数说明:sigmoid函数
"""
def sigmoid(inX):
	return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
"""
def gradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
    weights = np.ones(n)  #参数初始化
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小，每次减小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))  #随机选取样本
            h = sigmoid(sum(dataMatrix[randIndex]*weights)) 
            error = classLabels[randIndex] - h  #计算误差
            weights = weights + alpha * error * dataMatrix[randIndex]#更新回归系数
            del(dataIndex[randIndex])  #删除已经使用的样本
    return weights 
"""
函数说明:绘制数据集
"""
def plotBestFit(weights):
	dataMat, labelMat = loadDataSet()									
	dataArr = np.array(dataMat)									
	n = np.shape(dataMat)[0]										
	xcord1 = []; ycord1 = []											
	xcord2 = []; ycord2 = []											
	for i in range(n):	
		if int(labelMat[i]) == 1:
			xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
		else:
			xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
	fig = plt.figure()
	ax = fig.add_subplot(111)										
	ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)
	ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)
	x = np.arange(-3.0, 3.0, 0.1)
	y = (-weights[0] - weights[1] * x) / weights[2]
	ax.plot(x, y)
	plt.xlabel('X1'); plt.ylabel('X2')
	plt.show()		

if __name__ == '__main__':
	dataMat, labelMat = loadDataSet()	
	weights = gradAscent(np.array(dataMat), labelMat)
	plotBestFit(weights)
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:梯度上升算法测试函数
求函数f(x) = -x^2 + 4x的极大值
"""
def Gradient_Ascent_test():
	def f_prime(x_old):	#f(x)的导数
		return -2 * x_old + 4
	x_old = -1	#初始值，给一个小于x_new的值
	x_new = 0	#梯度上升算法初始值，即从(0,0)开始
	alpha = 0.01#步长，也就是学习速率，控制更新的幅度
	presision = 0.00000001	#精度，也就是更新阈值
	while abs(x_new - x_old) > presision:
		x_old = x_new
		x_new = x_old + alpha * f_prime(x_old)#上面提到的公式
	print(x_new)#打印最终求解的极值近似值
"""
函数说明:加载数据
"""
def loadDataSet():
	dataMat = []	#创建数据列表
	labelMat = []	#创建标签列表
	fr = open('testSet.txt')#打开文件	
	for line in fr.readlines():	#逐行读取
		lineArr = line.strip().split()列表
		dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#添加数据
		labelMat.append(int(lineArr[2]))
	fr.close()
	return dataMat, labelMat
"""
函数说明:sigmoid函数
"""
def sigmoid(inX):
	return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
"""
def gradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
    weights = np.ones(n)  #参数初始化
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小，每次减小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))  #随机选取样本
            h = sigmoid(sum(dataMatrix[randIndex]*weights)) 
            error = classLabels[randIndex] - h  #计算误差
            weights = weights + alpha * error * dataMatrix[randIndex]#更新回归系数
            del(dataIndex[randIndex])  #删除已经使用的样本
    return weights 
"""
函数说明:绘制数据集
"""
def plotBestFit(weights):
	dataMat, labelMat = loadDataSet()									
	dataArr = np.array(dataMat)									
	n = np.shape(dataMat)[0]										
	xcord1 = []; ycord1 = []											
	xcord2 = []; ycord2 = []											
	for i in range(n):	
		if int(labelMat[i]) == 1:
			xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
		else:
			xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
	fig = plt.figure()
	ax = fig.add_subplot(111)										
	ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)
	ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)
	x = np.arange(-3.0, 3.0, 0.1)
	y = (-weights[0] - weights[1] * x) / weights[2]
	ax.plot(x, y)
	plt.xlabel('X1'); plt.ylabel('X2')
	plt.show()		

if __name__ == '__main__':
	dataMat, labelMat = loadDataSet()	
	weights = gradAscent(np.array(dataMat), labelMat)
	plotBestFit(weights)

总结

Logistic回归

• 优点：计算代价不高，易于理解和实现
• 缺点：容易欠拟合，分类精准可能不高
• 适用数据类型：整数型和标称型数据

Logistic回归的一般过程

• 收集数据：采用任意方法收集数据。
• 准本数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳。
• 分析数据：采用任意方法对数据进行分析。
• 训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数。
• 测试算法：一旦训练步骤完成，分类将会很快。
• 使用算法：首先，我们需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定它们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作。