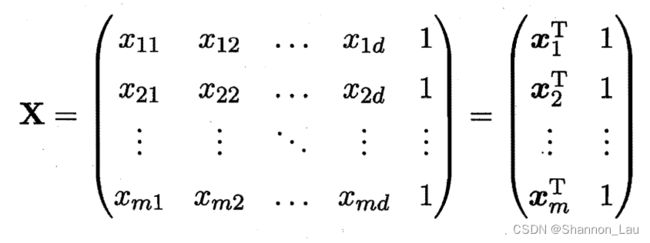《西瓜书》阅读笔记——第三章
3.1基本形式
给定由 d d d个属性描述的示例 x = ( x 1 ; x 2 ; . . . ; x d ) x=(x_1;x_2;...;x_d) x=(x1;x2;...;xd)其中 x i x_i xi均是 x x x在第 i i i个属 性上的取值,线性模型(linear model) 试图学得一个通过属性的线性组合来进行 预测的函数,即 : f ( x ) = ω 1 x 1 + ω 3 x 2 + . . . + ω d x d + b f(x)=\omega_1x_1+\omega_3x_2+...+\omega_dx_d+b f(x)=ω1x1+ω3x2+...+ωdxd+b
一般用向量形式: f ( x ) = ω T x + b f(x)=\omega^Tx+b f(x)=ωTx+b 其中 ω = ( ω 1 ; ω 2 ; . . . ; ω d ) \omega=(\omega_1;\omega_2;...;\omega_d) ω=(ω1;ω2;...;ωd)
-
许多功能更为强大的非线性模型(nonlinear model) 可在线性模型的基础上通过引入层级结构或高维映射而得.
-
ω \omega ω直观地表达了个属性的权重,因此线性模型有很好的可解释性 (comprehensibility)
f 好 瓜 ( x ) = 0.2 × x 色 泽 + 0.5 × x 根 蒂 + 0.3 × x 敲 声 + 1 f_{好瓜}(x)=0.2×x_{色泽} +0.5×x_{根蒂} +0.3×x_{敲声} +1 f好瓜(x)=0.2×x色泽+0.5×x根蒂+0.3×x敲声+1
即:判断是否为好瓜时,根蒂地占比很大
3.2 线性回归
数据集:
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\} D={(x1,y1),(x2,y2),...,(xm,ym)}
其中 x i = ( x i 1 ; x i 2 ; . . . ; x i d ) x_i=(x_{i1};x_{i2};...;x_{id}) xi=(xi1;xi2;...;xid) y i ∈ R y_i \in R yi∈R
- 线性回归" (linear regression): 图学得一个线性模型以尽可能准确地预测实值输出标记.
3.2.1 一元线性模型
输入属性的数目只有一个
此时的数据集 D = { ( x i , y i ) } i = 1 m , x i ∈ R D=\{(x_i,y_i)\}_{i=1}^m,x_i\in R D={(xi,yi)}i=1m,xi∈R
对于离散属性:
- 存在“序(order)”关系: 转换为连续值。
- 二值属性"身高"的取值"高" "矮"可转化为 {1.0, 0.0};
- 三值属性"高度" 的取值"高" “中” "低"可转化为 {1.0, 0.5, 0.0};
- 不存在序关系:转换为k维向量
- “西瓜”:(0,0,1)
- “南瓜”:(0,1,0)
- “黄瓜”:(1,0,0)
线性回归目标是:学得 f ( x i ) = ω x i + b f(x_i)=\omega x_i+b f(xi)=ωxi+b 使得 $ f(x_i) \backsimeq y_i.$
- 均方误差:对应了欧氏距离(Euclidean distance).。
- 最小二乘法(least square method):基于均方误差最小化来进行模型求解的方法。
在线性回归中,最小二乘法就是找到一条直线,使所有样本到直线上的欧氏距离之和最小.
- 参数估计(pameter estimation):求解 ω 和 b \omega和b ω和b使得 E ( ω , b ) = ∑ i = 1 m ( y i − ω x i − b ) 2 E_{(\omega,b)}=\sum_{i=1}^m(y_i-\omega x_i-b)^2 E(ω,b)=∑i=1m(yi−ωxi−b)2最小化的过程。
将 E ( ω , b ) E_{(\omega,b)} E(ω,b)分别对 ω , b \omega ,b ω,b求导得:
令上式均为0,可得到 ω 和 b \omega和b ω和b最优解的闭式(closed-form)解

注: x ‾ = 1 m ∑ i = 1 m x i \overline{x}=\frac{1}{m}\displaystyle \sum_{i=1}^mx_i x=m1i=1∑mxi为 x x x的均值
3.2.2 多元线性回归(multivariate linear regression)
同样使用最小二乘法对 ω \omega ω和 b b b进行估计。
简化:
-
把 b b b放到 ω \omega ω的右侧构成一个新的矩 ω ^ = ( ω ; b ) \hat{\omega}=(\omega;b) ω^=(ω;b)
-
将lable也写成向量形式: y = ( y i ; y x ; . . . ; y m ) y=(y_i;y_x;...;y_m) y=(yi;yx;...;ym),则有

令 E ω ^ = ( y − X ω ^ ) T ( y − X ω ^ ) E_{\hat{\omega}}=(y-X\hat{\omega})^T(y-X{\hat{\omega}}) Eω^=(y−Xω^)T(y−Xω^),对 ω \omega ω求导: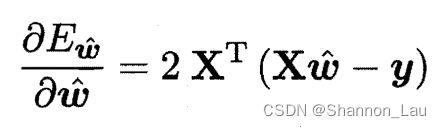 (假设 X T X X^TX XTX为满秩矩阵或正定矩阵):
(假设 X T X X^TX XTX为满秩矩阵或正定矩阵):
令上式为0,求得 ω ^ \hat{\omega} ω^最优解的闭式解: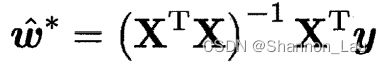
最后学得模型:
在现实任务中 X T X X^TX XTX往往不是满秩矩阵或正定矩阵(变量数远超样例数),导致矩阵 X X X的列数多于行数,此时的最优解 ω ^ \hat{\omega} ω^不唯一,最后选择哪一个解,由学习算法的归纳偏好决定,常见的做法是引入正则化(regularization)项。
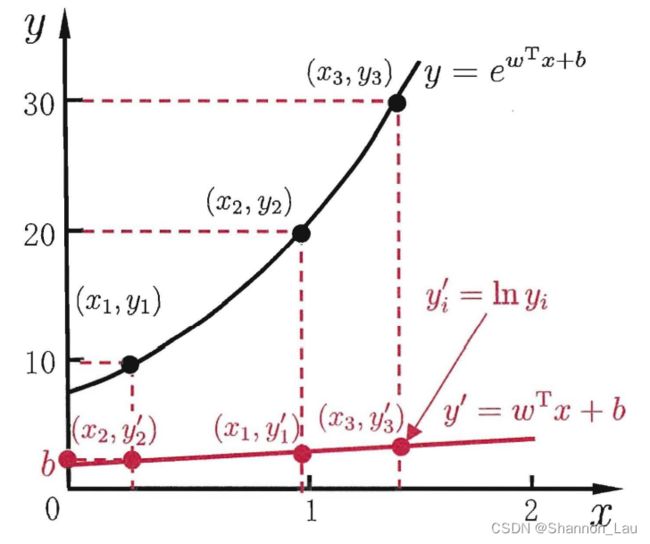
3.2.3 对数线性回归(log-linear regression )
为了便于观察,将线性回归模型简写为: y = ω T x + b y=\omega^Tx+b y=ωTx+b
假设我们认为示例所对应的输 出标记是在指数尺度上变化,那就可将输出标记的对数作为线性模型逼近的目
标: ln y = ω T x + b \ln y=\omega^Tx+b lny=ωTx+b.
-
广义线性模型(generalized linear model): y = g − 1 ( ω T x + b ) y=g^{-1}(\omega^Tx+b) y=g−1(ωTx+b)
-
联系函数(link function): g ( ⋅ ) g(·) g(⋅) 连续且充分光滑
对数线性回归是广义线性模型在 g ( ⋅ ) = ln ( ⋅ ) g(·)=\ln(·) g(⋅)=ln(⋅)时的特例。
3.3 对数几率回归
对于二分类任务,输出空间为 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1};而线性回归模型的预测值 z = ω T x + b z=\omega^Tx+b z=ωTx+b是实数,于是要转换为0/1值。这里最理想的是单位阶跃函数(unit-step function)
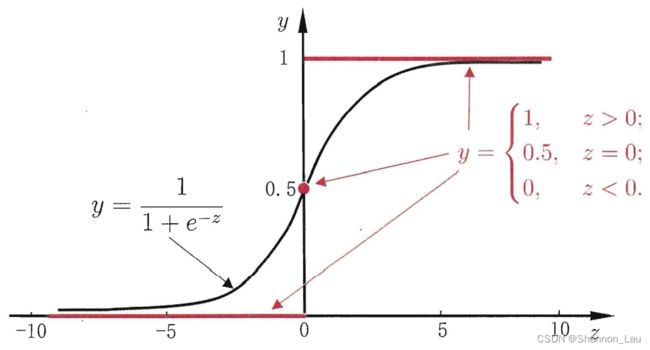 z > 0:正例
z > 0:正例
z < 0:负例
z = 0:任意
单位阶跃函数不连续,因此不能直接用于 g − ( ⋅ ) g^-(·) g−(⋅). 于是我们希望找到能在一定程度上近似单位阶跃函数的"替 代函数" (surrogate function) ,并希望它单调可微.
对数几率函数(logistic function) 正是这样一个常用的替代函数: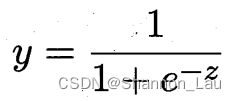
他是Sigmoid函数。
将 g − ( ⋅ ) g^-(·) g−(⋅)带入Sigmoid函数:

变形为: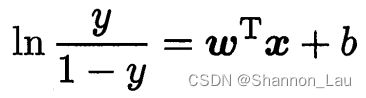
- 对数几率(logit): ln y 1 − y \ln \frac{y}{1-y} ln1−yy
上式是在线性回归的预测结果的基础上毕竟真实标记的对数几率,因此称为“对数几率回归”(logistic regression,亦称logit regression).
注意:他虽然叫做“回归”实际上是一种分类方法。
将 ln y 1 − y = ω T x + b \ln\frac{y}{1-y}=\omega^Tx+b ln1−yy=ωTx+b中的y视为后验概率估计 p ( y = 1 ∣ x ) p(y=1|x) p(y=1∣x)则有: ln p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = ω T x + b \ln\frac{p(y=1|x)}{p(y=0|x)}=\omega^Tx+b lnp(y=0∣x)p(y=1∣x)=ωTx+b,显然有: