评分卡模型构建(含泪总结精华!!)
五 评分卡模型构建
学习目标
-
掌握KS值的计算方法
-
知道评分映射方法
-
知道XGBoost和LightGBM基本原理
-
掌握使用lightGBM进行特征筛选的方法
-
应用toad构建评分卡模型
1 模型构建流程
1.1 实验设计
-
新的模型能上线一定要比原有方案有提升,需要通过实验证明
冷启动 业务初期 成长期 波动期 策略调整 新增数据源 人工审核 人工审核 新旧模型对比 新旧模型对比 避免迭代模型 新旧模型对比 规则模型 标准模型 长短表现期对比 稳定和波动人群 线上模型、陪跑 和标准模型对比 数据驱动模型 上一版模型 -
业务逐渐稳定后,人工审核是否会去掉
-
一般算法模型上线后,在高分段和低分段模型表现较好,中间的用户可能需要人工参与审核
-
模型表现越来越好之后,人工审核的需求会逐步降低,但不会去掉
-
-
标准模型:逻辑回归,随机森林
-
策略和模型不会同时调整
-
1.2 样本设计
-
ABC卡观察期,表现期
| 观察期 | 表现期 | |
|---|---|---|
| 实时A卡 | 申请时点往前6~12个月 | FPD7,FPD30 |
| 白名单A卡 | 邀请时点/激活时点往前6~12个月 | FPD30 |
| B卡 | 当前未逾期用户任意用信时点前6~12个月 | 当期/后续2-6期DPD30/DPD60 |
| C卡 | 当前逾期未还用户还款日后1天/30天/60天往前6~12个月 | 当期DPD30/60/90 |
-
还款状态和DPD一起刻画了用户的逾期情况
| 还款日前(Before Due) | 还款日后(After Due) | |
|---|---|---|
| 完全还款(Fully Repay) | FB(好用户) | FA(催回来了) |
| 部分还款(Patially Repay) | PB | PA(有意愿,但无力完全还款) |
| 展期(Extend) | EB(提前展期) | EA (违约后展期,可能是高危用户) |
| 未还款(Not Repay) | NB | NA |
-
A卡 申请新客 B卡未逾期老客 C卡 逾期老客
-
当前逾期:出现逾期且到观测点为止未还清 NA,PA
-
历史逾期:曾经出现过逾期已还清或当前逾期 FA,NA,PA
-
举例
-
一月 二月 三月 四月 五月 还款状态 还清 还清 还清 还清 还清 DPD 40 0 0 0 0 上面情况属于B卡客户
-
一月 二月 三月 四月 五月 还款状态 还清 还清 还清 还清 未还 DPD 0 0 0 0 40 上面情况属于C卡客户
-
一月 二月 三月 四月 五月 还款状态 还清 还清 还清 未还 未还 DPD 40 0 0 40 10 上面情况属于C卡客户
-
-
样本设计表格
-
训练集 测试集 1月 2月 3月 4月 5月 6月 7月 8月 总# 100 200 300 400 500 600 700 800 坏# 3 6 6 8 15 12 14 24 坏% 3% 3% 2% 2% 3% 2% 2% 3% -
观察坏样本的比例,不要波动过大
-
客群描述:首单用户、内部数据丰富、剔除高危职业、收入范围在XXXX
-
客群标签:好: FPD<=30 坏: FPD>30
-
1.3 模型训练与评估
-
目前还是使用机器学习模型,少数公司在尝试深度学习
-
模型的可解释性>稳定性>区分度
-
区分度:AUC,KS
-
稳定性: PSI
-
-
业务指标:通过率,逾期率
-
逾期率控制在比较合理的范围的前提下,要提高通过率
-
A卡,要保证一定过得通过率,对逾期率可以有些容忍
-
B卡,想办法把逾期率降下来,好用户提高额度
-
-
-
AUC:ROC曲线下的面积,反映了模型输出的概率对好坏用户的排序能力
-
KS反映了好坏用户的分布的最大的差别
-
ROC曲线是对TPR和FPR的数值对的记录
-
KS = max(TPR-FPR)
-
-
AUC和KS的区别可以简化为:
-
AUC反映模型区分度的平均状况
-
KS反映了模型区分度的最佳状况
-
-
PSI和特征里的PSI完全一样
1.4 模型上线整体流程
2 逻辑回归评分卡
2.1 评分映射方法
-
使用逻辑回归模型可以得到一个[0,1]区间的结果, 在风控场景下可以理解为用户违约的概率, 评分卡建模时我们需要把违约的概率映射为评分
-
举例:
-
用户的基础分为650分
-
当这个用户非逾期的概率是逾期的概率的2倍时,加50分
-
非逾期的概率是逾期的概率的4倍时,加100分
-
非逾期的概率是逾期的概率的8倍时,加150分
-
以此类推,就得到了业内标准的评分卡换算公式
-
-
$$score = 650+50 lg_2(P{正样本}/ P{负样本})$$
-
score是评分卡映射之后的输出,$P{正样本}$是样本非逾期的概率,$P{负样本}$是样本逾期的概率
-
-
逻辑回归评分卡如何与评分卡公式对应:
-
逻辑回归方程为
$$ln(P{正样本}/ P{负样本}) = w_1x_1+w_2x_2+w_3x_3+... ...$$
-
在信用评分模型建模时,逻辑回归的线性回归成分输出结果为$ln(P{正样本}/ P{负样本}) $,即对数似然。
-
由对数换底公式可知:
$$log_2(P{正样本}/ P{负样本}) = ln(P{正样本}/ P{负样本}) /ln2 = w_1x_1+w_2x_2+w_3x_3+... /ln2$$
只需要解出逻辑回归中每个特征的系数,然后将样本的每个特征值加权求和即可得到客户当前的标准化信用评分
-
-
基础分(Base Score)为650分,步长(Point of Double Odds,PDO)为50分,这两个值需要根据业务需求进行调整
-
2.2 逻辑回归评分卡
import pandas as pd
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
import numpy as np
import random
import math-
读取数据
data = pd.read_csv('data/Bcard.txt')
data.head()输出结果
obs_mth bad_ind uid td_score jxl_score mj_score rh_score zzc_score zcx_score person_info finance_info credit_info act_info 0 2018-10-31 0.0 A10000005 0.675349 0.144072 0.186899 0.483640 0.928328 0.369644 -0.322581 0.023810 0.00 0.217949 1 2018-07-31 0.0 A1000002 0.825269 0.398688 0.139396 0.843725 0.605194 0.406122 -0.128677 0.023810 0.00 0.423077 2 2018-09-30 0.0 A1000011 0.315406 0.629745 0.535854 0.197392 0.614416 0.320731 0.062660 0.023810 0.10 0.448718 3 2018-07-31 0.0 A10000481 0.002386 0.609360 0.366081 0.342243 0.870006 0.288692 0.078853 0.071429 0.05 0.179487 4 2018-07-31 0.0 A1000069 0.406310 0.405352 0.783015 0.563953 0.715454 0.512554 -0.261014 0.023810 0.00 0.423077
-
数据字段说明:
-
bad_ind 为标签
-
外部评分数据:td_score,jxl_score,mj_score,rh_score,zzc_score,zcx_score
-
内部数据: person_info, finance_info, credit_info, act_info
-
obs_month: 申请日期所在月份的最后一天(数据经过处理,将日期都处理成当月最后一天)
-
-
看一下月份分布,用最后一个月做为跨时间验证集
data.obs_mth.unique()输出结果
array(['2018-10-31', '2018-07-31', '2018-09-30', '2018-06-30',
'2018-11-30'], dtype=object)-
划分测试数据和验证数据(时间外样本)
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
val = data[data.obs_mth == '2018-11-30'].reset_index().copy()-
取出建模用到的特征
#info结尾的是自己做的无监督系统输出的个人表现,score结尾的是收费的外部征信数据
feature_lst = ['person_info','finance_info','credit_info','act_info','td_score','jxl_score','mj_score','rh_score']-
训练模型
x = train[feature_lst]
y = train['bad_ind']
val_x = val[feature_lst]
val_y = val['bad_ind']
lr_model = LogisticRegression(C=0.1)
lr_model.fit(x,y)输出结果
LogisticRegression(C=0.1, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
-
模型评价
-
ROC曲线:描绘的是不同的截断点时,并以FPR和TPR为横纵坐标轴,描述随着截断点的变小,TPR随着FPR的变化
-
纵轴:TPR=正例分对的概率 = TP/(TP+FN),其实就是查全率 召回
-
横轴:FPR=负例分错的概率 = FP/(FP+TN) 原本是0被预测为1的样本在所有0的样本中的概率
-
-
KS值
-
作图步骤:
-
根据学习器的预测结果(注意,是正例的概率值,非0/1变量)对样本进行排序(从大到小)-----这就是截断点依次选取的顺序 按顺序选取截断点,并计算TPR和FPR ---也可以只选取n个截断点,分别在1/n,2/n,3/n等位置 横轴为样本的占比百分比(最大100%),纵轴分别为TPR和FPR,可以得到KS曲线max(TPR-FPR)
-
ks = max(TPR-FPR)TPR和FPR曲线分隔最开的位置就是最好的”截断点“,最大间隔距离就是KS值,通常>0.2即可认为模型有比较好偶的预测准确性
-
-
-
绘制ROC计算KS
y_pred = lr_model.predict_proba(x)[:,1] #取出训练集预测值
fpr_lr_train,tpr_lr_train,_ = roc_curve(y,y_pred) #计算TPR和FPR
train_ks = abs(fpr_lr_train - tpr_lr_train).max() #计算训练集KS
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(val_x)[:,1] #计算验证集预测值
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred) #计算验证集预测值
val_ks = abs(fpr_lr - tpr_lr).max() #计算验证集KS值
print('val_ks : ',val_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR') #绘制训练集ROC
plt.plot(fpr_lr,tpr_lr,label = 'evl LR') #绘制验证集ROC
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()
显示结果:
train_ks : 0.4151676259891534 val_ks : 0.3856283523530577
-
使用lightgbm进行特征筛选
# lightgbm版本 3.0.0
import lightgbm as lgb
from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y = train_test_split(x,y,random_state=0,test_size=0.2)
def lgb_test(train_x,train_y,test_x,test_y):
clf =lgb.LGBMClassifier(boosting_type = 'gbdt',
objective = 'binary',
metric = 'auc',
learning_rate = 0.1,
n_estimators = 24,
max_depth = 5,
num_leaves = 20,
max_bin = 45,
min_data_in_leaf = 6,
bagging_fraction = 0.6,
bagging_freq = 0,
feature_fraction = 0.8,
)
clf.fit(train_x,train_y,eval_set = [(train_x,train_y),(test_x,test_y)],eval_metric = 'auc')
return clf,clf.best_score_['valid_1']['auc'],
lgb_model , lgb_auc = lgb_test(train_x,train_y,test_x,test_y)
feature_importance = pd.DataFrame({'name':lgb_model.booster_.feature_name(),
'importance':lgb_model.feature_importances_}).sort_values(by=['importance'],ascending=False)
显示结果:
feature_importance [1] training's auc: 0.759467 valid_1's auc: 0.753322 [2] training's auc: 0.809023 valid_1's auc: 0.805658 [3] training's auc: 0.809328 valid_1's auc: 0.803858 [4] training's auc: 0.810298 valid_1's auc: 0.801355 [5] training's auc: 0.814873 valid_1's auc: 0.807356 [6] training's auc: 0.816492 valid_1's auc: 0.809279 [7] training's auc: 0.820213 valid_1's auc: 0.809208 [8] training's auc: 0.823931 valid_1's auc: 0.812081 [9] training's auc: 0.82696 valid_1's auc: 0.81453 [10] training's auc: 0.827882 valid_1's auc: 0.813428 [11] training's auc: 0.828881 valid_1's auc: 0.814226 [12] training's auc: 0.829577 valid_1's auc: 0.813749 [13] training's auc: 0.830406 valid_1's auc: 0.813156 [14] training's auc: 0.830843 valid_1's auc: 0.812973 [15] training's auc: 0.831587 valid_1's auc: 0.813501 [16] training's auc: 0.831898 valid_1's auc: 0.813611 [17] training's auc: 0.833751 valid_1's auc: 0.81393 [18] training's auc: 0.834139 valid_1's auc: 0.814532 [19] training's auc: 0.835177 valid_1's auc: 0.815209 [20] training's auc: 0.837368 valid_1's auc: 0.815205 [21] training's auc: 0.837946 valid_1's auc: 0.815099 [22] training's auc: 0.839585 valid_1's auc: 0.815602 [23] training's auc: 0.840781 valid_1's auc: 0.816105 [24] training's auc: 0.841174 valid_1's auc: 0.816869
name importance 6 person_info 65 8 credit_info 57 9 act_info 55 7 finance_info 50 4 zzc_score 46 5 zcx_score 44 2 mj_score 39 0 td_score 34 3 rh_score 34 1 jxl_score 32
-
模型调优,去掉几个特征,重新建模
#确定新的特征
feature_lst = ['person_info','finance_info','credit_info','act_info']
x = train[feature_lst]
y = train['bad_ind']
val_x = val[feature_lst]
val_y = val['bad_ind']
lr_model = LogisticRegression(C=0.1)
lr_model.fit(x,y)
y_pred = lr_model.predict_proba(x)[:,1]
fpr_lr_train,tpr_lr_train,_ = roc_curve(y,y_pred)
train_ks = abs(fpr_lr_train - tpr_lr_train).max()
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(val_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(val_y,y_pred)
val_ks = abs(fpr_lr - tpr_lr).max()
print('val_ks : ',val_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR')
plt.plot(fpr_lr,tpr_lr,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()
显示结果:
train_ks : 0.41573985983413414 val_ks : 0.3928959732014397
-
打印回归系数
# 系数
print('变量名单:',feature_lst)
print('系数:',lr_model.coef_)
print('截距:',lr_model.intercept_)
输出结果
变量名单: ['person_info', 'finance_info', 'credit_info', 'act_info'] 系数: [[ 2.48386162 4.44901224 1.88254182 -1.43356854]] 截距: [-3.90631899]
-
生成报告
计算出报告中所需要的字段:KS值、负样本个数、正样本个数、负样本累计个数、正样本累计个数、捕获率、负样本占比
#准备数据
bins = 20
temp_ = pd.DataFrame() #创建空白DataFrame
temp_['bad_rate_predict'] = lr_model.predict_proba(val_x)[:,1] # 预测结果(坏人概率)
temp_['real_bad'] = val_y # 真实结果
temp_ = temp_.sort_values('bad_rate_predict',ascending = False)#按照预测坏人概率降序排列
temp_['num'] = [i for i in range(temp_.shape[0])] #添加序号列,用于分组
temp_['num'] = pd.cut(temp_.num,bins = bins,labels = [i for i in range(bins)])#分成20组,为每组添加组号
#创建报告
report = pd.DataFrame()#创建空白DataFrame
#计算每一组坏人数量
report['BAD'] = temp_.groupby('num').real_bad.sum().astype(int)
#计算每一组好人数量
report['GOOD'] = temp_.groupby('num').real_bad.count().astype(int)-report['BAD']
#累计求和坏人数量
report['BAD_CNT'] = report['BAD'].cumsum()
#累计求和好人数量
report['GOOD_CNT'] = report['GOOD'].cumsum()
good_total = report.GOOD_CNT.max()
bad_total = report.BAD_CNT.max()
#计算到当前组坏人比例(占所有坏人比例)
report['BAD_PCTG'] = round(report.BAD_CNT/bad_total,3)
#计算当前组坏人概率
report['BADRATE'] =report.apply(lambda x: round(x.BAD/(x.BAD+x.GOOD),3),axis = 1)
#计算KS值
def cal_ks(x):
#当前箱累计坏人数量/总坏人数量 - 当前箱累计好人数量/好人数量
ks = (x.BAD_CNT/bad_total)-(x.GOOD_CNT/good_total)
return round(math.fabs(ks),3)
report['KS'] = report.apply(cal_ks,axis = 1)
report
输出结果:
num BAD GOOD BAD_CNT GOOD_CNT BAD_PCTG BADRATE KS 0 69 730 69 730 0.210 0.086 0.164 1 50 749 119 1479 0.363 0.063 0.268 2 35 764 154 2243 0.470 0.044 0.326 3 31 767 185 3010 0.564 0.039 0.372 4 19 780 204 3790 0.622 0.024 0.380 5 18 781 222 4571 0.677 0.023 0.385 6 15 783 237 5354 0.723 0.019 0.380 7 14 785 251 6139 0.765 0.018 0.373 8 17 782 268 6921 0.817 0.021 0.375 9 6 793 274 7714 0.835 0.008 0.342 10 8 790 282 8504 0.860 0.010 0.316 11 6 793 288 9297 0.878 0.008 0.284 12 7 792 295 10089 0.899 0.009 0.255 13 10 788 305 10877 0.930 0.013 0.235 14 7 792 312 11669 0.951 0.009 0.205 15 5 794 317 12463 0.966 0.006 0.170 16 4 794 321 13257 0.979 0.005 0.131 17 4 795 325 14052 0.991 0.005 0.093 18 1 798 326 14850 0.994 0.001 0.045 19 2 797 328 15647 1.000 0.003 0.000
从报告中可以看出
① 模型的KS最大值出现在第6箱(编号5),如将箱分的更细,KS值会继续增大,上限为前面通过公式计算出的KS值
② 前4箱的样本占总人数的20%,捕捉负样本占所有负样本的56.4%,如拒绝分数最低的20%的人,可以捕捉到56.4%的负样本。
-
Pyecharts绘图,绘制负样本占比和KS值,观察模型表现
from pyecharts.charts import *
from pyecharts import options as opts
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
np.set_printoptions(suppress=True)
pd.set_option('display.unicode.ambiguous_as_wide', True)
pd.set_option('display.unicode.east_asian_width', True)
line = (
Line()
.add_xaxis(report.index.values.tolist())
.add_yaxis(
"分组坏人占比",
list(report.BADRATE),
yaxis_index=0,
color="red",
)
.set_global_opts(
title_opts=opts.TitleOpts(title="评分卡模型表现"),
)
.extend_axis(
yaxis=opts.AxisOpts(
name="KS值",
type_="value",
min_=0,
max_=0.5,
position="right",
axisline_opts=opts.AxisLineOpts(
linestyle_opts=opts.LineStyleOpts(color="red")
),
axislabel_opts=opts.LabelOpts(formatter="{value}"),
)
)
.add_yaxis(
"KS",
list(report['KS']),
yaxis_index=1,
color="blue",
label_opts=opts.LabelOpts(is_show=False),
)
)
line.render_notebook()
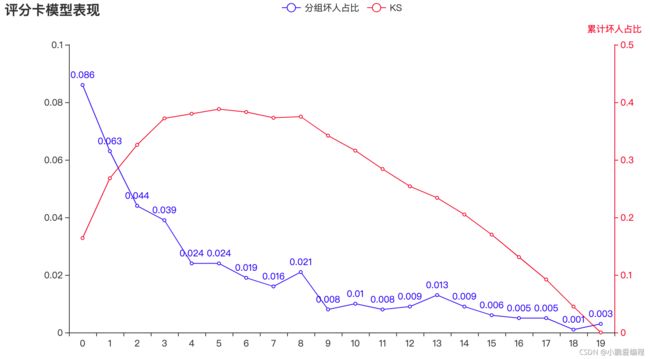
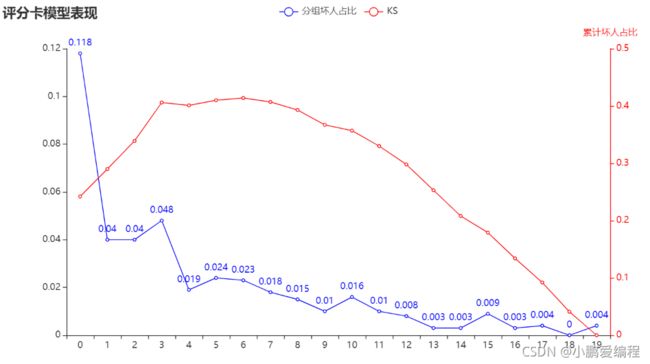
输出结果:
-
图中蓝色曲线为负样本占比曲线,红色曲线为KS曲线
-
模型在第8箱的位置出现了波动,即第8箱的负样本占比高于第7箱
-
虽然曲线图中有多处波动,但幅度不大,总体趋势较为平稳。因此模型的排序能力仍可被业务所接受。
-
-
评分映射
#['person_info','finance_info','credit_info','act_info']
def score(person_info,finance_info,credit_info,act_info):
xbeta = person_info * ( 2.48386162) + finance_info * ( 4.44901224 ) + credit_info * (1.88254182) + act_info * ( -1.43356854) --3.90631899
score = 900-50* (xbeta)/math.log(2) # 基准分+ 系数* 2^(1-p/p)
return score
val['score'] = val.apply(lambda x : score(x.person_info,x.finance_info,x.credit_info,x.act_info) ,axis=1)
fpr_lr,tpr_lr,_ = roc_curve(val_y,val['score'])
val_ks = abs(fpr_lr - tpr_lr).max()
print('val_ks : ',val_ks)
输出结果:
val_ks : 0.3928959732014397
-
划分评级:可以通过分数段对客群进行划分,得到每一个级别用户的逾期率
#对应评级区间
def level(score):
level = 0
if score <= 600:
level = "D"
elif score <= 640 and score > 600 :
level = "C"
elif score <= 680 and score > 640:
level = "B"
elif score > 680 :
level = "A"
return level
val['level'] = val.score.map(lambda x : level(x) )
val.level.groupby(val.level).count()/len(val)
输出结果
level A 0.121064 B 0.256463 C 0.376463 D 0.246009 Name: level, dtype: float64
-
如果希望某个区间的逾期率更大或者更小,可以调整评分映射函数中的基础分和系数
3 集成学习评分卡
3.1 Gradient Boosting算法回顾
-
基本原理
-
训练一个模型m1,产生错误e1
-
针对e1训练一个模型m2,产生错误e2
-
针对e2训练第三个模型m3,产生错误e3 .....
-
最终预测结果是:m1+m2+m3+.....
-
-
GBDT是boosting的一种方法,主要思想:
-
每一次建立单个分类器时,是在之前建立的模型的损失函数的梯度下降方向。
-
损失函数越大,说明模型越容易出错,如果我们的模型能让损失函数持续的下降,则说明我们的模型在持续不断的改进,而最好的方式就是让损失函数在其梯度的方向上下降。
-
GBDT的核心在于每一棵树学的是之前所有树结论和的残差
-
残差就是真实值与预测值的差值
-
为了得到残差,GBDT中的树全部是回归树,不用分类树
-
-
Shrinkage(缩减)是 GBDT 的一个重要演进分支
-
Shrinkage的思想在于每次走一小步来逼近真实的结果,比直接迈大步的方式好
-
Shrinkage可以有效减少过拟合的风险。它认为每棵树只学到了一小部分,累加的时候只累加这一小部分,通过多学习几棵树来弥补不足。这累加的一小部分(步长*残差)来逐步逼近目标,所以各个树的残差是渐变的而不是陡变的。
-
-
GBDT可以用于回归问题(线性和非线性),也可用于分类问题
-
-
GBDT和随机森林的异同点
-
相同点:
-
都是由多棵树构成,最终的结果也是由多棵树决定。
-
-
不同点:
-
随机森林可以由分类树和回归树组成,GBDT只能由回归树组成。
-
随机森林的树可以并行生成,而GBDT只能串行生成,所以随机森林的训练速度相对较快。
-
随机森林关注减小模型的方差,GBDT关注减小模型的偏差。
-
随机森林对异常值不敏感,GBDT对异常值非常敏感。
-
随机森林最终的结果是多数投票或简单平均,而GBDT是加权累计起来。
-
-
-
GBDT的优缺点
-
优点:
-
GBDT每一次的残差计算都增大了分错样本的权重,而分对的权重都趋近于0,因此泛化性能比较好。
-
可以灵活的处理各种类型的数据。
-
预测精度高
-
-
缺点:
-
对异常值比较敏感。
-
由于分类器之间存在依赖关系,所以很难进行并行计算。
-
-
3.2 XGBOOST
-
XGBoost简介
-
XGBoost的全称是eXtreme Gradient Boosting,原理与GBDT相同
-
它是经过优化的分布式梯度提升库,旨在高效、灵活且可移植
-
XGBoost是大规模并行boosting tree的工具,比GBDT更高效
-
-
XGBoost与GDBT的区别
-
区别一:
-
XGBoost生成CART树考虑了树的复杂度,
-
GDBT未考虑,GDBT在树的剪枝步骤中考虑了树的复杂度。
-
-
区别二:
-
XGBoost是拟合上一轮损失函数的二阶导展开,GDBT是拟合上一轮损失函数的一阶导展开,因此,XGBoost的准确性更高,且满足相同的训练效果,需要的迭代次数更少。
-
-
区别三:
-
XGBoost与GDBT都是逐次迭代来提高模型性能,但是XGBoost在选取最佳切分点时可以开启多线程进行,大大提高了运行速度。
-
-
-
xgboost 案例
-
皮马印第安人糖尿病数据集(预测是否会得糖尿病) :
-
Pregnancies:怀孕次数
-
Glucose:葡萄糖
-
BloodPressure:血压 (mm Hg)
-
SkinThickness:皮层厚度 (mm)
-
Insulin:胰岛素 2小时血清胰岛素(mu U / ml )
-
BMI:体重指数 (体重/身高)^2
-
DiabetesPedigreeFunction:糖尿病谱系功能
-
Age:年龄 (岁)
-
Outcome:目标值 (0或1)
-
-
#加载数据
import pandas as pd
data = pd.read_csv('Pima-Indians-Diabetes.csv')
data.head()
Out[8]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | Outcome | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
-
xgboost参数
-
n_estimators:梯度提升树的棵数,也就是拟合几次残差
-
learning rate:一般情况下,学习速率的值为0.1。但是,对于不同的问题,理想的学习速率有时候会在0.05到0.3之间波动。
-
正则化参数
-
reg_alpha L1正则化系数
-
reg_lambda L2正则化系数
-
-
max_depth [default=6]
-
用于设置树的最大深度
-
range: [1,∞]
-
-
subsample [default=1]
-
表示观测的子样本的比率,将其设置为0.5意味着xgboost将随机抽取一半观测用于数的生长,这将有助于防止过拟合现象
-
range: (0,1]
-
-
min_child_weight [default=1]
-
表示子树观测权重之和的最小值,如果树的生长时的某一步所生成的叶子结点,其观测权重之和小于min_child_weight,那么可以放弃该步生长,在线性回归模式中,这仅仅与每个结点所需的最小观测数相对应。该值越大,算法越保守
-
range: [0,∞]
-
-
colsample_bytree [default=1]
-
表示用于构造每棵树时变量的子样本比率
-
range: (0,1]
-
-
-
使用Xgboost 的 Sklearn接口
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import pandas as pd
import pickle
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.externals import joblib
# 用pandas读入数据
data = pd.read_csv('Pima-Indians-Diabetes.csv')
# 做数据切分
train, test = train_test_split(data)
# 取出特征X和目标y的部分
feature_columns = ['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI', 'DiabetesPedigreeFunction', 'Age']
target_column = 'Outcome'
train_X = train[feature_columns].values
train_y = train[target_column].values
test_X = test[feature_columns].values
test_y = test[target_column].values
# 初始化模型
xgb_classifier = xgb.XGBClassifier(n_estimators=20,\
max_depth=4, \
learning_rate=0.1, \
subsample=0.7, \
colsample_bytree=0.7)
# 拟合模型
xgb_classifier.fit(train_X, train_y)
# 使用模型预测
preds = xgb_classifier.predict(test_X)
# 判断准确率
print ('错误类为%f' %((preds!=test_y).sum()/float(test_y.shape[0])))
# 模型存储
joblib.dump(xgb_classifier, '2.model')
错误类为0.229167
显示结果
['0002.model']
-
early-stopping 早停:在训练集上学习模型,一颗一颗树添加,在验证集上看效果,当验证集效果不再提升,停止树的添加与生长
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn import datasets
digits = datasets.load_digits(n_class=2)
X = digits['data']
y = digits['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = xgb.XGBClassifier()
clf.fit(X_train, y_train, early_stopping_rounds=10, eval_metric="auc",
eval_set=[(X_test, y_test)])
显示结果:
[0] validation_0-auc:0.99950 Will train until validation_0-auc hasn't improved in 10 rounds. [1] validation_0-auc:0.99975 [2] validation_0-auc:0.99975 [3] validation_0-auc:0.99975 [4] validation_0-auc:0.99975 [5] validation_0-auc:0.99975 [6] validation_0-auc:1.00000 [7] validation_0-auc:1.00000 [8] validation_0-auc:1.00000 [9] validation_0-auc:1.00000 [10] validation_0-auc:1.00000 [11] validation_0-auc:1.00000 [12] validation_0-auc:1.00000 [13] validation_0-auc:1.00000 [14] validation_0-auc:1.00000 [15] validation_0-auc:1.00000 [16] validation_0-auc:1.00000 Stopping. Best iteration: [6] validation_0-auc:1.00000XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1, colsample_bynode=1, colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0, max_depth=3, min_child_weight=1, missing=None, n_estimators=100, n_jobs=1, nthread=None, objective='binary:logistic', random_state=0, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None, silent=None, subsample=1, verbosity=1)
-
使用Xgboost输出特征重要程度
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn import datasets
iris = datasets.load_iris()
y = iris['target']
X = iris['data']
xgb_model = xgb.XGBClassifier().fit(X,y)
temp = pd.DataFrame()
temp['feature_names'] = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
temp['feature_importances'] = xgb_model.feature_importances_
temp = temp.sort_values('feature_importances',ascending = False)
temp
显示结果:
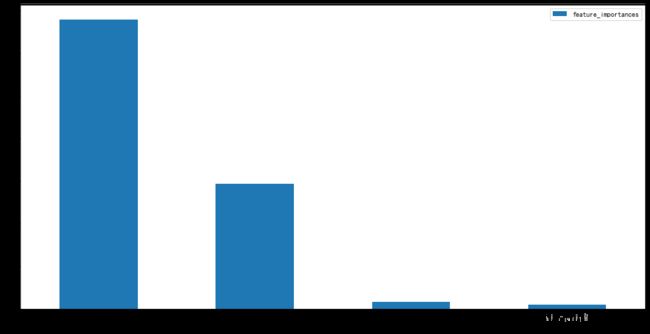
feature_names feature_importances 2 petal_length 0.679664 3 petal_width 0.294529 1 sepal_width 0.016569 0 sepal_length 0.009238
temp.set_index('feature_names').plot.bar(figsize=(16,8),rot=0)
显示结果:
3.3 LightGBM
1 什么是lightGBM
lightGBM是2017年1月,微软在GItHub上开源的一个新的梯度提升框架。
github介绍链接
在开源之后,就被别人冠以“速度惊人”、“支持分布式”、“代码清晰易懂”、“占用内存小”等属性。
LightGBM主打的高效并行训练让其性能超越现有其他boosting工具。在Higgs数据集上的试验表明,LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6。
higgs数据集介绍:这是一个分类问题,用于区分产生希格斯玻色子的信号过程和不产生希格斯玻色子的信号过程。
数据链接
2 lightGBM原理
lightGBM 主要基于以下方面优化,提升整体特特性:
-
基于Histogram(直方图)的决策树算法
-
Lightgbm 的Histogram(直方图)做差加速
-
带深度限制的Leaf-wise的叶子生长策略
-
直接支持类别特征
-
直接支持高效并行
具体解释见下,分节介绍。
基于Histogram(直方图)的决策树算法
直方图算法的基本思想是
-
先把连续的浮点特征值离散化成k个整数,同时构造一个宽度为k的直方图。
-
在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
Eg:
[0, 0.1) --> 0;
[0.1,0.3) --> 1;
...
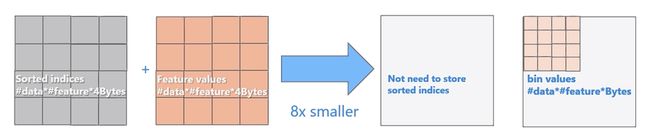
使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。
然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data#feature)优化到O(k#features)。
当然,Histogram算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在不同的数据集上的结果表明,离散化的分割点对最终的精度影响并不是很大,甚至有时候会更好一点。原因是决策树本来就是弱模型,分割点是不是精确并不是太重要;较粗的分割点也有正则化的效果,可以有效地防止过拟合;即使单棵树的训练误差比精确分割的算法稍大,但在梯度提升(Gradient Boosting)的框架下没有太大的影响。
Lightgbm 的Histogram(直方图)做差加速
一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。
通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
带深度限制的Leaf-wise的叶子生长策略
Level-wise遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。
-
但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。
-
因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。
-
Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
直接支持类别特征
实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。
而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。
在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。目前来看,LightGBM是第一个直接支持类别特征的GBDT工具。
Expo数据集介绍:数据包含1987年10月至2008年4月美国境内所有商业航班的航班到达和离开的详细信息。这是一个庞大的数据集:总共有近1.2亿条记录。主要用于预测航班是否准时。
数据链接
直接支持高效并行
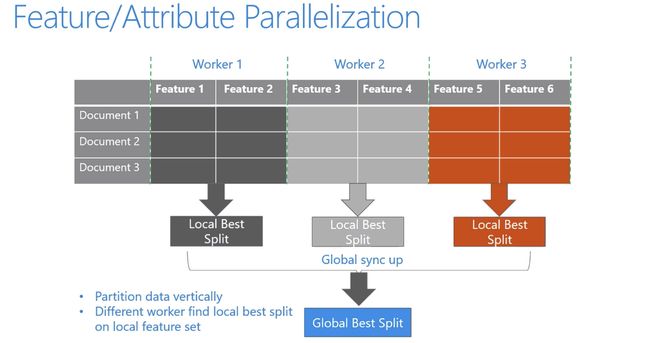
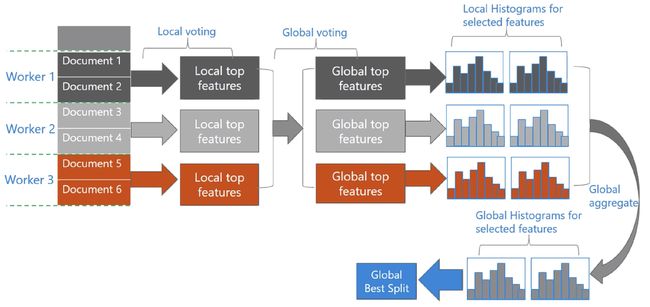
LightGBM还具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
-
特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点,然后在机器间同步最优的分割点。
-
数据并行则是让不同的机器先在本地构造直方图,然后进行全局的合并,最后在合并的直方图上面寻找最优分割点。
LightGBM针对这两种并行方法都做了优化:
-
在特征并行算法中,通过在本地保存全部数据避免对数据切分结果的通信;
-
在数据并行中使用分散规约 (Reduce scatter) 把直方图合并的任务分摊到不同的机器,降低通信和计算,并利用直方图做差,进一步减少了一半的通信量。
-
基于投票的数据并行(Voting Parallelization)则进一步优化数据并行中的通信代价,使通信代价变成常数级别。在数据量很大的时候,使用投票并行可以得到非常好的加速效果。
3.4 LightGBM特征筛选
import pandas as pd
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
import numpy as np
import random
import math
import time
import lightgbm as lgb
data = pd.read_csv('data/Bcard.txt')
data.head()
显示结果
obs_mth bad_ind uid td_score jxl_score mj_score rh_score zzc_score zcx_score person_info finance_info credit_info act_info 0 2018-10-31 0.0 A10000005 0.675349 0.144072 0.186899 0.483640 0.928328 0.369644 -0.322581 0.023810 0.00 0.217949 1 2018-07-31 0.0 A1000002 0.825269 0.398688 0.139396 0.843725 0.605194 0.406122 -0.128677 0.023810 0.00 0.423077 2 2018-09-30 0.0 A1000011 0.315406 0.629745 0.535854 0.197392 0.614416 0.320731 0.062660 0.023810 0.10 0.448718 3 2018-07-31 0.0 A10000481 0.002386 0.609360 0.366081 0.342243 0.870006 0.288692 0.078853 0.071429 0.05 0.179487 4 2018-07-31 0.0 A1000069 0.406310 0.405352 0.783015 0.563953 0.715454 0.512554 -0.261014 0.023810 0.00 0.423077
-
采用相同的方式划分测试集验证集
df_train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
val = data[data.obs_mth == '2018-11-30'].reset_index().copy()
-
使用LightGBM的特征重要性以及夸时间交叉验证方式进行特征筛选
-
将数据按时间排序
-
df_train = df_train.sort_values(by = 'obs_mth',ascending = False)
df_train.head()
显示结果
index obs_mth bad_ind uid td_score jxl_score mj_score rh_score zzc_score zcx_score person_info finance_info credit_info act_info 0 0 2018-10-31 0.0 A10000005 0.675349 0.144072 0.186899 0.483640 0.928328 0.369644 -0.322581 0.023810 0.00 0.217949 33407 33407 2018-10-31 0.0 A2810176 0.146055 0.079922 0.250568 0.045240 0.766906 0.413713 0.013863 0.023810 0.00 0.269231 33383 33383 2018-10-31 0.0 A2807687 0.551366 0.300781 0.225007 0.045447 0.735733 0.684182 -0.261014 0.071429 0.03 0.269231 33379 33379 2018-10-31 0.0 A2807232 0.708547 0.769513 0.928457 0.739716 0.947453 0.361551 -0.128677 0.047619 0.00 0.269231 33376 33376 2018-10-31 0.0 A2806932 0.482248 0.116658 0.286273 0.056618 0.047024 0.890433 0.078853 0.047619 0.00 0.269231
-
将数据按照时间先后顺序分成5组
df_train['rank'] = [i for i in range(df_train.shape[0])]
df_train['rank'] = pd.cut(df_train['rank'],bins = 5,labels = [i for i in range(5)])
df_train.head()
显示结果
index obs_mth bad_ind uid td_score jxl_score mj_score rh_score zzc_score zcx_score person_info finance_info credit_info act_info rank 0 0 2018-10-31 0.0 A10000005 0.675349 0.144072 0.186899 0.483640 0.928328 0.369644 -0.322581 0.02381 0.00 0.217949 1 56822 56822 2018-10-31 0.0 A5492021 0.645511 0.058839 0.543122 0.235281 0.633456 0.186917 -0.053718 0.02381 0.10 0.166667 1 56991 56991 2018-10-31 0.0 A560974 0.299629 0.344316 0.500635 0.245191 0.056203 0.084314 0.078853 0.02381 0.03 0.538462 1 56970 56970 2018-10-31 0.0 A55912 0.929199 0.347249 0.438309 0.188931 0.611842 0.485462 -0.322581 0.02381 0.05 0.743590 1 57520 57520 2018-10-31 0.0 A601797 0.149059 0.803444 0.167015 0.264857 0.208072 0.704634 -0.261014 0.02381 0.00 0.525641 1
-
查看分组后,每组的数据量
df_train['rank'].value_counts()
显示结果
0 15967 4 15966 3 15966 2 15966 1 15966 Name: num, dtype: int64
-
查看数据总量,与每组相加结果吻合
len(df_train)
显示结果
79831
-
使用lgbm进行分组交叉特征筛选
#定义lgb函数
def LGB_test(train_x,train_y,test_x,test_y):
from multiprocessing import cpu_count
clf = lgb.LGBMClassifier(
boosting_type='gbdt', num_leaves=31, reg_alpha=0.0, reg_lambda=1,
max_depth=2, n_estimators=800,max_features = 140, objective='binary',
subsample=0.7, colsample_bytree=0.7, subsample_freq=1,
learning_rate=0.05, min_child_weight=50,random_state=None,n_jobs=cpu_count()-1,
num_iterations = 800 #迭代次数
)
clf.fit(train_x, train_y,eval_set=[(train_x, train_y),(test_x,test_y)],eval_metric='auc',early_stopping_rounds=100)
print(clf.n_features_)
return clf,clf.best_score_[ 'valid_1']['auc']
feature_lst = []
ks_train_lst = []
ks_test_lst = []
for rk in set(df_train['rank']):
# 0,1,2,3,4,
#定义模型训练集与测试集
ttest = df_train[df_train['rank'] == rk]
ttrain = df_train[df_train['rank'] != rk]
train = ttrain[lst]
train_y = ttrain.bad_ind
test = ttest[lst]
test_y = ttest.bad_ind
model,auc = LGB_test(train,train_y,test,test_y)
#模型贡献度放在feture中
feature = pd.DataFrame(
{'name' : model.booster_.feature_name(),
'importance' : model.feature_importances_
}).set_index('name')
feature_lst.append(feature)
#计算训练集、测试集、验证集上的KS和AUC
y_pred_train_lgb = model.predict_proba(train)[:, 1]
y_pred_test_lgb = model.predict_proba(test)[:, 1]
train_fpr_lgb, train_tpr_lgb, _ = roc_curve(train_y, y_pred_train_lgb)
test_fpr_lgb, test_tpr_lgb, _ = roc_curve(test_y, y_pred_test_lgb)
train_ks = abs(train_fpr_lgb - train_tpr_lgb).max()
test_ks = abs(test_fpr_lgb - test_tpr_lgb).max()
train_auc = metrics.auc(train_fpr_lgb, train_tpr_lgb)
test_auc = metrics.auc(test_fpr_lgb, test_tpr_lgb)
ks_train_lst.append(train_ks)
ks_test_lst.append(test_ks)
train_ks = np.mean(ks_train_lst)
test_ks = np.mean(ks_test_lst)
print('train_ks: ',train_ks)
print('test_ks: ',test_ks)
显示结果:
train_ks: 0.49076511891289665 test_ks: 0.4728837205200532
feature_importance = pd.concat(feature_lst,axis = 1).mean(1).sort_values(ascending = False)
feature_importance[(feature_importance>20)].index.tolist()
显示结果:
['finance_info', 'person_info', 'credit_info', 'act_info']
3.5 LightGBM评分卡
-
最终筛选出4个特征
lst = ['person_info','finance_info','credit_info','act_info']
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
evl = data[data.obs_mth == '2018-11-30'].reset_index().copy()
x = train[lst]
y = train['bad_ind']
evl_x = evl[lst]
evl_y = evl['bad_ind']
model,auc = LGB_test(x,y,evl_x,evl_y)
y_pred = model.predict_proba(x)[:,1]
fpr_lgb_train,tpr_lgb_train,_ = roc_curve(y,y_pred)
train_ks = abs(fpr_lgb_train - tpr_lgb_train).max()
print('train_ks : ',train_ks)
y_pred = model.predict_proba(evl_x)[:,1]
fpr_lgb,tpr_lgb,_ = roc_curve(evl_y,y_pred)
evl_ks = abs(fpr_lgb - tpr_lgb).max()
print('evl_ks : ',evl_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_lgb_train,tpr_lgb_train,label = 'train LR')
plt.plot(fpr_lgb,tpr_lgb,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()
显示结果:
train_ks : 0.49356612822896156 evl_ks : 0.435912868827033
-
从结果中看出,LightGBM效比LR要好,但LR通过一些处理,模型表现也会有提升
-
将集成学习评分卡结果转换成分数
def score(xbeta):
score = 600+50*(math.log2((1-xbeta)/xbeta)) #好人的概率/坏人的概率
return score
evl['xbeta'] = model.predict_proba(evl_x)[:,1]
evl['score'] = evl.apply(lambda x : score(x.xbeta) ,axis=1)
evl['score']
显示结果
0 799.044524 1 981.994370 2 911.925133 3 907.718692 4 981.994370 ... 15970 761.518532 15971 901.987537 15972 901.987537 15973 883.922367 15974 785.625330 Name: score, Length: 15975, dtype: float64
-
用转换的分数验证KS值
fpr,tpr,_ = roc_curve(val_y,evl['score'])
val_ks = abs(fpr - tpr).max()
val_ks
显示结果
0.43591286882703295
-
生成模型报告
#准备数据
bins = 20
temp_ = pd.DataFrame() #创建空白DataFrame
temp_['bad_rate_predict'] = evl['score'] # 预测结果(坏人概率)
temp_['real_bad'] = val_y # 真实结果
temp_ = temp_.sort_values('bad_rate_predict')#按照预测坏人概率降序排列
temp_['num'] = [i for i in range(temp_.shape[0])] #添加序号列,用于分组
temp_['num'] = pd.cut(temp_.num,bins = bins,labels = [i for i in range(bins)])#分成20组,为每组添加组号
#创建报告
report = pd.DataFrame()#创建空白DataFrame
#计算每一组坏人数量
report['BAD'] = temp_.groupby('num').real_bad.sum().astype(int)
#计算每一组好人数量
report['GOOD'] = temp_.groupby('num').real_bad.count().astype(int)-report['BAD']
#累计求和坏人数量
report['BAD_CNT'] = report['BAD'].cumsum()
#累计求和好人数量
report['GOOD_CNT'] = report['GOOD'].cumsum()
good_total = report.GOOD_CNT.max()
bad_total = report.BAD_CNT.max()
#计算到当前组坏人比例(占所有坏人比例)
report['BAD_PCTG'] = round(report.BAD_CNT/bad_total,3)
#计算当前组坏人概率
report['BADRATE'] =report.apply(lambda x: round(x.BAD/(x.BAD+x.GOOD),3),axis = 1)
#计算KS值
def cal_ks(x):
#当前箱累计坏人数量/总坏人数量 - 当前箱累计好人数量/好人数量
ks = (x.BAD_CNT/bad_total)-(x.GOOD_CNT/good_total)
return round(math.fabs(ks),3)
report['KS'] = report.apply(cal_ks,axis = 1)
report
显示结果
num BAD GOOD BAD_CNT GOOD_CNT BAD_PCTG BADRATE KS 0 95 704 95 704 0.290 0.119 0.245 1 32 767 127 1471 0.387 0.040 0.293 2 31 768 158 2239 0.482 0.039 0.339 3 35 763 193 3002 0.588 0.044 0.397 4 18 781 211 3783 0.643 0.023 0.402 5 24 775 235 4558 0.716 0.030 0.425 6 16 782 251 5340 0.765 0.020 0.424 7 11 788 262 6128 0.799 0.014 0.407 8 11 788 273 6916 0.832 0.014 0.390 9 14 785 287 7701 0.875 0.018 0.383 10 9 789 296 8490 0.902 0.011 0.360 11 7 792 303 9282 0.924 0.009 0.331 12 4 795 307 10077 0.936 0.005 0.292 13 6 792 313 10869 0.954 0.008 0.260 14 3 796 316 11665 0.963 0.004 0.218 15 3 796 319 12461 0.973 0.004 0.176 16 4 794 323 13255 0.985 0.005 0.138 17 1 798 324 14053 0.988 0.001 0.090 18 2 797 326 14850 0.994 0.003 0.045 19 2 797 328 15647 1.000 0.003 0.000
-
pyecharts绘图展示模型表现
from pyecharts.charts import *
from pyecharts import options as opts
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
np.set_printoptions(suppress=True)
pd.set_option('display.unicode.ambiguous_as_wide', True)
pd.set_option('display.unicode.east_asian_width', True)
line = (
Line()
.add_xaxis(list(report.index))
.add_yaxis(
"分组坏人占比",
list(report.BADRATE),
yaxis_index=0,
color="red",
)
.set_global_opts(
title_opts=opts.TitleOpts(title="评分卡模型表现"),
)
.extend_axis(
yaxis=opts.AxisOpts(
name="累计坏人占比",
type_="value",
min_=0,
max_=0.5,
position="right",
axisline_opts=opts.AxisLineOpts(
linestyle_opts=opts.LineStyleOpts(color="red")
),
axislabel_opts=opts.LabelOpts(formatter="{value}"),
)
)
.add_yaxis(
"KS",
list(report['KS']),
yaxis_index=1,
color="blue",
label_opts=opts.LabelOpts(is_show=False),
)
)
line.render_notebook()
显示结果:
4 整体流程梳理
1 加载数据
import pandas as pd
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import numpy as np
import math
import xgboost as xgb
import toad
# 加载数据
data_all = pd.read_csv("scorecard.txt")
# 指定不参与训练列名
ex_lis = ['uid', 'samp_type', 'bad_ind']
# 参与训练列名
ft_lis = list(data_all.columns)
for i in ex_lis:
ft_lis.remove(i)
# 开发样本、验证样本与时间外样本
dev = data_all[(data_all['samp_type'] == 'dev')]
val = data_all[(data_all['samp_type'] == 'val') ]
off = data_all[(data_all['samp_type'] == 'off') ]
-
探索性数据分析,同时处理数值型和字符型
toad.detector.detect(data_all)
显示结果:
type size missing unique mean_or_top1 std_or_top2 min_or_top3 1%_or_top4 10%_or_top5 50%_or_bottom5 75%_or_bottom4 90%_or_bottom3 99%_or_bottom2 max_or_bottom1 bad_ind float64 95806 0.00% 2 0.0187671 0.135702 0 0 0 0 0 0 1 1 uid object 95806 0.00% 95806 Ab99_96002866062686144:0.00% A7511004:0.00% A10729014:0.00% A8502810:0.00% A594541:0.00% A8899777:0.00% A10150838:0.00% A3044048:0.00% A1888452:0.00% A7659794:0.00% td_score float64 95806 0.00% 95806 0.499739 0.288349 5.46966e-06 0.00961341 0.0997056 0.500719 0.747984 0.900024 0.990041 0.999999 jxl_score float64 95806 0.00% 95806 0.499338 0.28885 1.28155e-05 0.00994678 0.0991025 0.499795 0.748646 0.899703 0.989348 0.999985 mj_score float64 95806 0.00% 95806 0.50164 0.288679 6.92442e-06 0.0105076 0.100882 0.503048 0.752032 0.899308 0.990047 0.999993 rh_score float64 95806 0.00% 95806 0.498407 0.287797 5.00212e-06 0.00991632 0.0999483 0.497466 0.747188 0.899286 0.989473 0.999986 zzc_score float64 95806 0.00% 95806 0.500627 0.289067 1.15778e-05 0.0101856 0.0990114 0.501688 0.750986 0.899924 0.990043 0.999998 zcx_score float64 95806 0.00% 95806 0.499672 0.289137 9.97767e-06 0.0103249 0.0997429 0.49913 0.750683 0.901942 0.989712 0.999987 person_info float64 95806 0.00% 7 -0.078229 0.156859 -0.322581 -0.322581 -0.322581 -0.0537176 0.078853 0.078853 0.078853 0.078853 finance_info float64 95806 0.00% 35 0.0367625 0.0396866 0.0238095 0.0238095 0.0238095 0.0238095 0.0238095 0.0714286 0.214286 1.02381 credit_info float64 95806 0.00% 100 0.0636262 0.143098 0 0 0 0 0.06 0.18 0.8 1 act_info float64 95806 0.00% 74 0.236197 0.157132 0.0769231 0.0769231 0.0769231 0.205128 0.346154 0.487179 0.615385 1.08974 samp_type object 95806 0.00% 3 dev:68.16% off:16.67% val:15.16% None None None None dev:68.16% off:16.67% val:15.16%
2 特征筛选(缺失值,IV,相关系数)
-
使用缺失率、IV、相关系数进行特征筛选。但是考虑到后续建模过程要对变量进行分箱处理,该操作会使变量的IV变小,变量间的相关性变大,因此此处可以对IV和相关系的阈值限制适当放松,或不做限制
dev_slct1, drop_lst= toad.selection.select(dev, dev['bad_ind'],
empty=0.7, iv=0.03,
corr=0.7,
return_drop=True,
exclude=ex_lis)
print("keep:", dev_slct1.shape[1],
"drop empty:", len(drop_lst['empty']),
"drop iv:", len(drop_lst['iv']),
"drop corr:", len(drop_lst['corr']))
显示结果:
keep: 12 drop empty: 0 drop iv: 1 drop corr: 0
3 卡方分箱
# 得到切分节点
combiner = toad.transform.Combiner()
combiner.fit(dev_slct1, dev_slct1['bad_ind'], method='chi',
min_samples=0.05, exclude=ex_lis)
# 导出箱的节点
bins = combiner.export()
print(bins)
显示结果:
{'td_score': [0.7989831262724624], 'jxl_score': [0.4197048501965005], 'mj_score': [0.3615303943747963], 'zzc_score': [0.4469861520889339], 'zcx_score': [0.7007847486465795], 'person_info': [-0.2610139784946237, -0.1286774193548387, -0.05371756272401434, 0.013863440860215051, 0.06266021505376344, 0.07885304659498207], 'finance_info': [0.047619047619047616], 'credit_info': [0.02, 0.04, 0.11], 'act_info': [0.1153846153846154, 0.14102564102564102, 0.16666666666666666, 0.20512820512820512, 0.2692307692307692, 0.35897435897435903, 0.3974358974358974, 0.5256410256410257]}
4 Bivar图,调整分箱
-
画图观察每个变量在开发样本和时间外样本上的Bivar图,为方便阅读,这里只以单变量act_info做示范
# 根据节点实施分箱
dev_slct2 = combiner.transform(dev_slct1)
val2 = combiner.transform(val[dev_slct1.columns])
off2 = combiner.transform(off[dev_slct1.columns])
# 分箱后通过画图观察
from toad.plot import bin_plot, badrate_plot
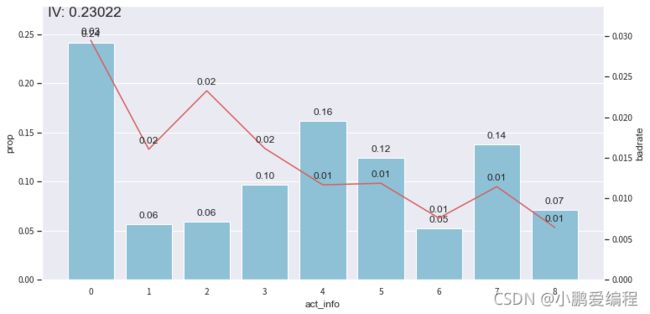
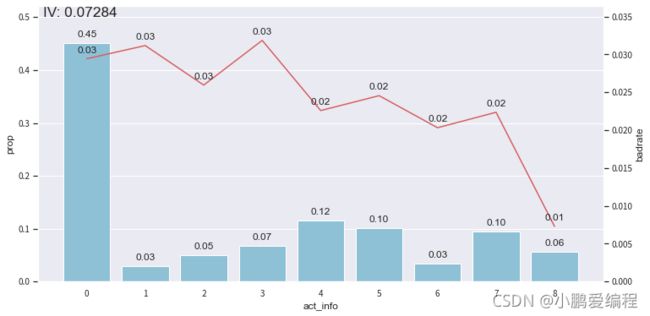
bin_plot(dev_slct2, x='act_info', target='bad_ind')
bin_plot(val2, x='act_info', target='bad_ind')
bin_plot(off2, x='act_info', target='bad_ind')
开发样本:
测试样本:
跨时间样本:
-
由于前3箱的变化趋势与整体不符(整体为递减趋势),因此在接下来的步骤中将其合并。第4~6箱合并,最后3箱进行合并。从而得到严格递减的变化趋势。
bins['act_info']
显示结果:
[0.1153846153846154, 0.14102564102564102, 0.16666666666666666, 0.20512820512820512, 0.2692307692307692, 0.35897435897435903, 0.3974358974358974, 0.5256410256410257]
adj_bin = {'act_info': [0.16666666666666666,0.35897435897435903,]}
combiner.set_rules(adj_bin)
dev_slct3 = combiner.transform(dev_slct1)
val3 = combiner.transform(val[dev_slct1.columns])
off3 = combiner.transform(off[dev_slct1.columns])
# 画出Bivar图
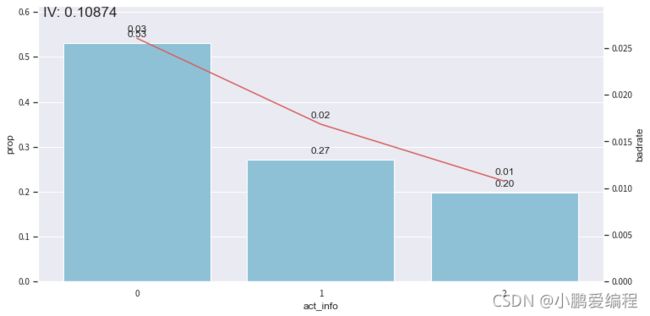
bin_plot(dev_slct3, x='act_info', target='bad_ind')
bin_plot(val3, x='act_info', target='bad_ind')
bin_plot(off3, x='act_info', target='bad_ind')
显示结果:
开发样本
测试样本
验证样本
5 绘制负样本占比关联图
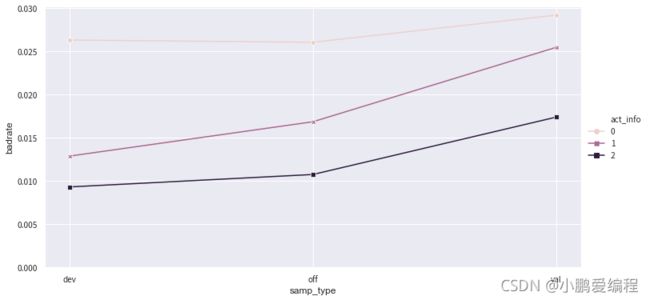
data = pd.concat([dev_slct3,val3,off3], join='inner')
badrate_plot(data, x='samp_type', target='bad_ind', by='act_info')
显示结果:
-
上图中,图中的线没有交叉,故不需要对该特征的分组进行合并,即使有少量交叉也不会对结果造成明显的影响,只有当错位比较严重的情况下才进行调整
data = pd.concat([dev_slct3,val3,off3], join='inner')
badrate_plot(data, x='samp_type', target='bad_ind', by='person_info')
显示结果:
-
上图中,有变量错位情况,属于可以容忍范围,也可以考虑将变量person_info中编号为3,4,5的箱合并
6 WOE编码,并验证IV
t = toad.transform.WOETransformer()
dev_slct3_woe = t.fit_transform(dev_slct3, dev_slct3['bad_ind'],
exclude=ex_lis)
val_woe = t.transform(val3[dev_slct3.columns])
off_woe = t.transform(off3[dev_slct3.columns])
data = pd.concat([dev_slct3_woe, val_woe, off_woe])
-
计算训练样本与测试样本的PSI
psi_df = toad.metrics.PSI(dev_slct3_woe, val_woe).sort_values(0)
psi_df = psi_df.reset_index()
psi_df = psi_df.rename(columns = {'index': 'feature', 0: 'psi'})
psi_df
显示结果:
feature psi 0 uid 0.000000e+00 1 samp_type 0.000000e+00 2 td_score 8.778656e-07 3 zcx_score 4.183912e-06 4 jxl_score 2.901553e-05 5 zzc_score 3.764148e-05 6 mj_score 5.005908e-05 7 bad_ind 4.128345e-03 8 credit_info 9.489392e-02 9 act_info 1.237395e-01 10 person_info 1.278102e-01 11 finance_info 1.341445e-01
-
删除PSI大于0.13的特征
-
通常单个特征的PSI值建议在0.1以下,根据具体情况可以适当调整
-
本案例数据为演示数据变量PSI普遍较大,因此选择0.13作为阈值
-
psi_013 = list(psi_df[psi_df.psi<0.13].feature)
# 避免不参与计算的几个特征被删掉,把 uid,samp_type,bad_ind添加回来并去重
psi_013.extend(ex_lis)
psi_013 = list(set(psi_013))
data = data[psi_013]
dev_woe_psi = dev_slct3_woe[psi_013]
val_woe_psi = val_woe[psi_013]
off_woe_psi = off_woe[psi_013]
print(data.shape)
显示结果:
(95806, 11)
-
卡方分箱后部分变量的IV降低,且整体相关程度增大,需要再次筛选特征
-
使用的IV和相关系数阈值较实际建模场景都偏小,主要是因为演示数据并非真实数据
-
dev_woe_psi2, drop_lst = toad.selection.select(dev_woe_psi,
dev_woe_psi['bad_ind'],
empty=0.6,
iv=0.001,
corr=0.5,
return_drop=True,
exclude=ex_lis)
print("keep:", dev_woe_psi2.shape[1],
"drop empty:", len(drop_lst['empty']),
"drop iv:", len(drop_lst['iv']),
"drop corr:", len(drop_lst['corr']))
显示结果:
keep: 7 drop empty: 0 drop iv: 4 drop corr: 0
7 特征筛选
-
使用逐步回归进行特征筛选,使用线性回归模型,并选择KS作为评价指标
-
estimator: 用于拟合的模型,支持'ols', 'lr', 'lasso', 'ridge'
-
direction: 逐步回归的方向,支持'forward', 'backward', 'both' (推荐)
-
Forward selection:将自变量逐个引入模型,引入一个自变量后查看该模型是否发生显著性变化
-
如果发生了显著性变化,那么则将该变量引入模型中,否则忽略该变量,直至遍历所有变量
-
即将变量按照贡献度从大到小排列,依次加入
-
-
Backward elimination:与Forward selection选择相反,将所有变量放入模型
-
尝试将某一变量进行剔除,查看剔除后对整个模型是否有显著性变化
-
如没有显著性变化则剔除,有则保留,直到留下所有对模型有显著性变化的因素
-
也就是将自变量按贡献度从小到大,依次剔除
-
-
both:将前向选择与后向消除同时进行
-
模型中每加入一个自变量,可能使某个已放入模型的变量显著性减小
-
显著性小于阈值时,可将该变量从模型中剔除
-
即每增加一个新的显著变量的同时,检验模型中所有变量的显著性,剔除不显著变量,从而得到最优变量组合
-
-
-
criterion: 评判标准,支持'aic', 'bic', 'ks', 'auc'
-
max_iter: 最大循环次数
-
return_drop: 是否返回被剔除的列名
-
exclude: 不需要被训练的列名,比如ID列和时间列
-
dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2,
dev_woe_psi2['bad_ind'],
exclude=ex_lis,
direction='both',
criterion='ks',
estimator='ols',
intercept=False)
val_woe_psi_stp = val_woe_psi[dev_woe_psi_stp.columns]
off_woe_psi_stp = off_woe_psi[dev_woe_psi_stp.columns]
data = pd.concat([dev_woe_psi_stp, val_woe_psi_stp, off_woe_psi_stp])
print(data.shape)
显示结果:
(95806, 6)
-
查看剩下的特征列
dev_woe_psi_stp.columns
显示结果:
Index(['uid', 'samp_type', 'bad_ind', 'credit_info', 'act_info', 'person_info'], dtype='object')
8 模型训练
-
定义函数用于模型训练
def lr_model(x, y, valx, valy, offx, offy, C):
model = LogisticRegression(C=C, class_weight='balanced')
model.fit(x,y)
y_pred = model.predict_proba(x)[:,1]
fpr_dev,tpr_dev,_ = roc_curve(y, y_pred)
train_ks = abs(fpr_dev - tpr_dev).max()
print('train_ks : ', train_ks)
y_pred = model.predict_proba(valx)[:,1]
fpr_val,tpr_val,_ = roc_curve(valy, y_pred)
val_ks = abs(fpr_val - tpr_val).max()
print('val_ks : ', val_ks)
y_pred = model.predict_proba(offx)[:,1]
fpr_off,tpr_off,_ = roc_curve(offy, y_pred)
off_ks = abs(fpr_off - tpr_off).max()
print('off_ks : ', off_ks)
from matplotlib import pyplot as plt
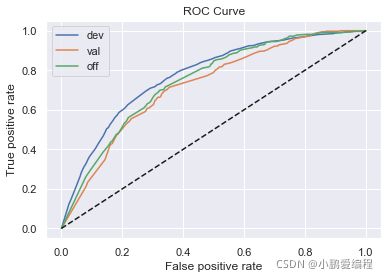
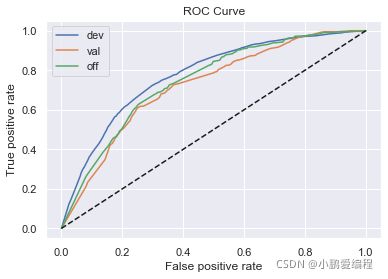
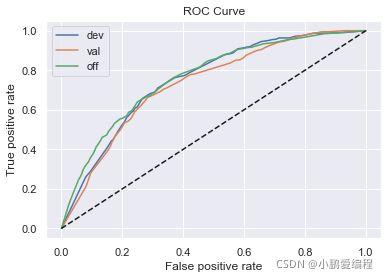
plt.plot(fpr_dev, tpr_dev, label='dev')
plt.plot(fpr_val, tpr_val, label='val')
plt.plot(fpr_off, tpr_off, label='off')
plt.plot([0,1], [0,1], 'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc='best')
plt.show()
def xgb_model(x, y, valx, valy, offx, offy):
model = xgb.XGBClassifier(learning_rate=0.05,
n_estimators=400,
max_depth=2,
class_weight='balanced',
min_child_weight=1,
subsample=1,
nthread=-1,
scale_pos_weight=1,
random_state=1,
n_jobs=-1,
reg_lambda=300)
model.fit(x, y)
y_pred = model.predict_proba(x)[:,1]
fpr_dev,tpr_dev,_ = roc_curve(y, y_pred)
train_ks = abs(fpr_dev - tpr_dev).max()
print('train_ks : ', train_ks)
y_pred = model.predict_proba(valx)[:,1]
fpr_val,tpr_val,_ = roc_curve(valy, y_pred)
val_ks = abs(fpr_val - tpr_val).max()
print('val_ks : ', val_ks)
y_pred = model.predict_proba(offx)[:,1]
fpr_off,tpr_off,_ = roc_curve(offy, y_pred)
off_ks = abs(fpr_off - tpr_off).max()
print('off_ks : ', off_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_dev, tpr_dev, label='dev')
plt.plot(fpr_val, tpr_val, label='val')
plt.plot(fpr_off, tpr_off, label='off')
plt.plot([0,1], [0,1], 'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc='best')
plt.show()
-
定义函数调用模型训练的方法
def bi_train(data, dep='bad_ind', exclude=None):
from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()
# 变量名
lis = list(data.columns)
for i in exclude:
lis.remove(i)
data[lis] = std_scaler.fit_transform(data[lis])
devv = data[(data['samp_type']=='dev')]
vall = data[(data['samp_type']=='val')]
offf = data[(data['samp_type']=='off')]
x, y = devv[lis], devv[dep]
valx, valy = vall[lis], vall[dep]
offx, offy = offf[lis], offf[dep]
# 逻辑回归正向
print("逻辑回归正向:")
lr_model(x, y, valx, valy, offx, offy, 0.1)
# 逻辑回归反向
print("逻辑回归反向:")
lr_model(offx, offy, valx, valy, x, y, 0.1)
# XGBoost正向
print("XGBoost正向:")
xgb_model(x, y, valx, valy, offx, offy)
# XGBoost反向
print("XGBoost反向:")
xgb_model(offx, offy, valx, valy, x, y)
-
上面函数中,XGBoost模型和逻辑回归模型各调用了两次,分别为正向调用和逆向调用
-
正向调用通过对开发样本的学习得到模型,并在时间外样本上检验效果
-
逆向调用使用时间外样本作为训练集,检验当前模型的效果上限
-
如逆向模型训练集KS值明显小于正向模型训练集KS值,说明当前时间外样本分布与开发样本差异较大,需要重新划分样本集。(样本量较小时经常发生)
-
-
调用上面函数
bi_train(data, dep='bad_ind', exclude=ex_lis)
显示结果:
逻辑回归正向: train_ks : 0.41733648227995124 val_ks : 0.3593935758405114 off_ks : 0.3758086175640308逻辑回归反向: train_ks : 0.3892612859630226 val_ks : 0.3717891855920369 off_ks : 0.4061965880072622XGBoost正向: train_ks : 0.42521927400747045 val_ks : 0.3595542266920359 off_ks : 0.37437103192850807XGBoost反向: train_ks : 0.3939473708822855 val_ks : 0.3799497614606668 off_ks : 0.3936270948436908
-
从结果中看出:
-
XGBoost模型的效果并没有明显高于逻辑回归模型,因此当前特征不需要再进行组合。
-
逆向调用LR模型的训练集结果,没有显著好于正向调用的时间外样本结果,该模型在当前特征空间下几乎没有更多的优化空间
-
正向LR模型的结果训练集KS值,与时间外样本KS值的差值在5%以内,故不需要调整跨时间稳定性较差的变量
-
9 计算指标评估模型,生成模型报告
-
假设当前模型已经进行过精细化调整了,接下来使用单个逻辑回归模型进行拟合。全部使用默认参数。
dep = 'bad_ind'
lis = list(data.columns)
for i in ex_lis:
lis.remove(i)
devv = data[data['samp_type']=='dev']
vall = data[data['samp_type']=='val']
offf = data[data['samp_type']=='off' ]
x, y = devv[lis], devv[dep]
valx, valy = vall[lis], vall[dep]
offx, offy = offf[lis], offf[dep]
lr = LogisticRegression()
lr.fit(x, y)
-
分别计算 F1-score KS和AUC
from toad.metrics import KS, F1, AUC
prob_dev = lr.predict_proba(x)[:,1]
print('训练集')
print('F1:', F1(prob_dev,y))
print('KS:', KS(prob_dev,y))
print('AUC:', AUC(prob_dev,y))
prob_val = lr.predict_proba(valx)[:,1]
print('跨时间')
print('F1:', F1(prob_val,valy))
print('KS:', KS(prob_val,valy))
print('AUC:', AUC(prob_val,valy))
prob_off = lr.predict_proba(offx)[:,1]
print('跨时间')
print('F1:', F1(prob_off,offy))
print('KS:', KS(prob_off,offy))
print('AUC:', AUC(prob_off,offy))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
print('特征PSI:','\n',toad.metrics.PSI(x,offx).sort_values(0))
显示结果:
训练集 F1: 0.02962459026532253 KS: 0.41406129833591426 AUC: 0.7713247123864264 验证集 F1: 0.027689429373246022 KS: 0.36127808343721585 AUC: 0.7225727568398459 跨时间 F1: 0.032454090150250414 KS: 0.3807135163445966 AUC: 0.7435613582904539 模型PSI: 0.34091667386100255 特征PSI: credit_info 0.098585 act_info 0.124820 person_info 0.127833 dtype: float64
-
生成模型时间外样本的KS报告
toad.metrics.KS_bucket(prob_off,offy,
bucket=15,
method='quantile')
显示结果:
min max bads goods total bad_rate good_rate odds bad_prop good_prop total_prop cum_bad_rate cum_bad_rate_rev cum_bads_prop cum_bads_prop_rev cum_goods_prop cum_goods_prop_rev cum_total_prop cum_total_prop_rev ks 0 0.001870 0.003187 2.0 963.0 965.0 0.002073 0.997927 0.002077 0.006098 0.061545 0.060407 0.002073 0.020532 0.006098 1.000000 0.061545 1.000000 0.060407 1.000000 0.055448 1 0.003791 0.004068 1.0 1054.0 1055.0 0.000948 0.999052 0.000949 0.003049 0.067361 0.066041 0.001485 0.021719 0.009146 0.993902 0.128906 0.938455 0.126448 0.939593 0.119760 2 0.004263 0.005382 3.0 793.0 796.0 0.003769 0.996231 0.003783 0.009146 0.050681 0.049828 0.002131 0.023289 0.018293 0.990854 0.179587 0.871094 0.176275 0.873552 0.161294 3 0.006361 0.008326 7.0 1341.0 1348.0 0.005193 0.994807 0.005220 0.021341 0.085703 0.084382 0.003122 0.024470 0.039634 0.981707 0.265290 0.820413 0.260657 0.823725 0.225656 4 0.008612 0.008761 6.0 958.0 964.0 0.006224 0.993776 0.006263 0.018293 0.061226 0.060344 0.003705 0.026670 0.057927 0.960366 0.326516 0.734710 0.321002 0.739343 0.268589 5 0.009022 0.010891 9.0 799.0 808.0 0.011139 0.988861 0.011264 0.027439 0.051064 0.050579 0.004717 0.028487 0.085366 0.942073 0.377580 0.673484 0.371581 0.678998 0.292215 6 0.011006 0.014774 17.0 1464.0 1481.0 0.011479 0.988521 0.011612 0.051829 0.093564 0.092707 0.006067 0.029883 0.137195 0.914634 0.471145 0.622420 0.464288 0.628419 0.333950 7 0.014807 0.018032 10.0 581.0 591.0 0.016920 0.983080 0.017212 0.030488 0.037132 0.036995 0.006868 0.033068 0.167683 0.862805 0.508276 0.528855 0.501283 0.535712 0.340593 8 0.018379 0.022200 44.0 2571.0 2615.0 0.016826 0.983174 0.017114 0.134146 0.164313 0.163693 0.009319 0.034266 0.301829 0.832317 0.672589 0.491724 0.664977 0.498717 0.370760 9 0.022235 0.030280 26.0 798.0 824.0 0.031553 0.968447 0.032581 0.079268 0.051000 0.051581 0.010920 0.042788 0.381098 0.698171 0.723589 0.327411 0.716557 0.335023 0.342492 10 0.030972 0.037582 33.0 1167.0 1200.0 0.027500 0.972500 0.028278 0.100610 0.074583 0.075117 0.012493 0.044832 0.481707 0.618902 0.798172 0.276411 0.791674 0.283443 0.316465 11 0.037968 0.058339 43.0 1007.0 1050.0 0.040952 0.959048 0.042701 0.131098 0.064357 0.065728 0.014675 0.051082 0.612805 0.518293 0.862530 0.201828 0.857402 0.208326 0.249725 12 0.062269 0.076029 42.0 908.0 950.0 0.044211 0.955789 0.046256 0.128049 0.058030 0.059468 0.016590 0.055751 0.740854 0.387195 0.920560 0.137470 0.916870 0.142598 0.179706 13 0.094398 0.094398 85.0 1243.0 1328.0 0.064006 0.935994 0.068383 0.259146 0.079440 0.083130 0.020532 0.064006 1.000000 0.259146 1.000000 0.079440 1.000000 0.083130 -0.000000
10 生成评分卡
-
将数据集合并后,利用ScoreCard函数重新训练并生成评分卡
-
该函数内嵌逻辑回归模型 参数 C '正则化强度', class_weight 与sklearn中逻辑回归参数一致
-
combiner: 传入训练好的 toad.Combiner 对象
-
transer: 传入先前训练的 toad.WOETransformer 对象
-
pdo、rate、base_odds、base_score: e.g. pdo=60, rate=2, base_odds=20,base_score=750 实际意义为当比率为1/20,输出基准评分750,当比率为基准比率2倍时,基准分下降60分
-
from toad.scorecard import ScoreCard
card = ScoreCard(combiner=combiner,
transer=t, C=0.1,
class_weight='balanced',
base_score=600,
base_odds=35,
pdo=60,
rate=2)
card.fit(x,y)
final_card = card.export(to_frame=True)
final_card
显示结果:
name value score 0 credit_info [-inf ~ 0.02) 158.04 1 credit_info [0.02 ~ 0.04) 122.51 2 credit_info [0.04 ~ 0.11) 73.94 3 credit_info [0.11 ~ inf) 43.98 4 act_info [-inf ~ 0.16666666666666666) 94.24 5 act_info [0.16666666666666666 ~ 0.35897435897435903) 115.71 6 act_info [0.35897435897435903 ~ inf) 125.38 7 person_info [-inf ~ -0.2610139784946237) 172.76 8 person_info [-0.2610139784946237 ~ -0.1286774193548387) 142.93 9 person_info [-0.1286774193548387 ~ -0.05371756272401434) 123.74 10 person_info [-0.05371756272401434 ~ 0.013863440860215051) 120.79 11 person_info [0.013863440860215051 ~ 0.06266021505376344) 108.83 12 person_info [0.06266021505376344 ~ 0.07885304659498207) 90.32 13 person_info [0.07885304659498207 ~ inf) 75.46
小结
-
掌握KS值的计算方法
-
KS= max(TPR-FPR)TPR和FPR曲线分隔最开的位置就是最好的”截断点“,
-
-
知道评分映射方法
-
$$score = 650+50 lg_2(P{正样本}/ P{负样本})$$
-
-
知道XGBoost和LightGBM基本原理
-
XGBoost 和 LightGBM 都基于GBDT
-
XGBoost在GBDT基础上做了二阶泰勒级数展开,效率更高,模型更精准
-
LightGBM在XGBoost基础上进一步优化,直接支持类别特征,直接支持高效并行,基于直方图的决策树算法效率更高
-
-
掌握使用lightGBM进行特征筛选的方法
-
利用lightGBM输出特征重要性
-
将样本用时间排序分组, 做跨时间交叉验证
-
-
应用toad构建评分卡模型
-
探索性数据分析
toad.detector.detect(data_all)-
特征筛选(缺失值,IV,相关系数)
dev_slct1, drop_lst= toad.selection.select(dev, dev['bad_ind'], empty=0.7, iv=0.03, corr=0.7, return_drop=True, exclude=ex_lis)-
Bivar图,观察变量单调性
combiner.transform(dev_slct1)-
负样本占比关联图
badrate_plot(data, x='samp_type', target='bad_ind', by='act_info')-
WOE
t = toad.transform.WOETransformer() dev_slct3_woe = t.fit_transform(dev_slct3, dev_slct3['bad_ind'], exclude=ex_lis)-
特征筛选
dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2, dev_woe_psi2['bad_ind'], exclude=ex_lis, direction='both', criterion='ks', estimator='ols', intercept=False)-
模型训练
-
生成模型报告
toad.metrics.KS_bucket(prob_off,offy, bucket=10, method='quantile')-
生成评分卡
from toad.scorecard import ScoreCard card = ScoreCard(combiner=combiner, transer=t, C=0.1, class_weight='balanced', base_score=600, base_odds=35, pdo=60, rate=2) -