朴素贝叶斯分类

机器学习的经典算法：朴素贝叶斯（naive byes）分类

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

一：贝叶斯原理

朴素贝叶斯分类算法是一个典型的统计学习方法，主要的理论基础就是贝叶斯公式。贝叶斯公式定义如下所示：

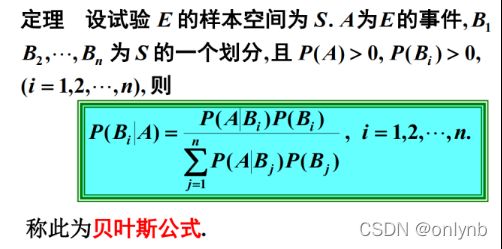
先验概率：通过经验来判断事情发生的概率。

后验概率：后验概率就是发生结果之后，推测原因的概率。

条件概率：事件 A 在另外一个事件 B 已经发生条件下的发生概率，表示为
P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。

P（A|B）表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：P（AB）/P(B)。但是在有些情况下，我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但是我们更想要知道P(B|A)。

例如（通信接收机检测判决）将A，B，C 三个字母之一输入信道，输出为原字母的概率为α，而输出为其它一字母的概率都是(1－α)/2。今将字母串AAAA，BBBB，CCCC 之一输入信道，输入AAAA，BBBB，CCCC 的概率分别为p1, p2, p3 (p1 +p2+p3=1)，已知输出为ABCA，问输入的是AAAA 的概率是多少？（设信道传输每个字母的工作是相互独立的。）在这个例子中，我们知道了结果，但是我们想要知道输入的概率，直接计算是非常困难的，但是通过贝叶斯公式就显得十分简单了。

换句话说，就是我们知道原因，推导结果是比较容易的，但是当我们知道结果，要反过来推导原因是十分困难的。而贝叶斯公式就为我们知道结果后推导原因提供了一个捷径。

二：朴素贝叶斯分类

在说完了贝叶斯原理之后，现在就来说朴素贝叶斯分类。

朴素贝叶斯分类之所以朴素，就是因为我们做了一个简单的假设，即类中特定特征的存在与任何其他特征的存在无关，这意味着每个特征彼此独立。因此对实际情况有所约束，如果属性之间存在关联，分类准确率会降低。不过在大多数应用的场景，朴素贝叶斯的分类效果都不错。

朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

朴素贝叶斯的定义如下：
1.设x={a1，a2，a3，……，an}为一个待分类项，而每个a为x的一个特征。
2.有类别集合c={y1，y2，y3，……，ym}
3.计算P(y1|x),P(y2|x），……，P(ym|x)
4.如果P(yk|x)=max{P(y1|x),P(y2|x），……，P(ym|x)},则x∈yk

那么现在的关键就是如何计算第3步中的各个条件概率。

1.找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2.统计得到在各类别下各个特征属性的条件概率估计。即：
P(a1|y1),P(a2|y1),……,P(an|y1);
P(a1|y2),P(a2|y2),……,P(an|y2);
……
P(a1|ym),P(a2|ym),……,P(an|ym);
3.假设各个特征属性是条件独立的，则根据贝叶斯原理有：
P(yi|x)=P(x|yi)P(yi)/p(x)
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有:
P(x|yi)P(yi)=P(a1|yi)P(a2|yi)……P(an|yi)P(yi);

朴素贝叶斯按照数据的先验概率的不同可以分为高斯朴素贝叶斯，伯努利朴素贝叶斯，多项式朴素贝叶斯。
1.高斯朴素贝叶斯
Gaussian Naive Bayes是指当特征属性为连续值时，而且分布服从高斯分布，那 么在计算P(x|y)的时候可以直接使用高斯分布的概率公式：

因此只需要计算出各个类别中此特征项划分的各个均值和标准差

2.伯努利朴素贝叶斯
Bernoulli Naive Bayes是指当特征属性为连续值时，而且分布服从伯努利分布， 那么在计算P(x|y)的时候可以直接使用伯努利分布的概率公式：

伯努利分布是一种离散分布，只有两种可能的结果。1表示成功，出现的概率为p； 0表示失败，出现的概率为q=1-p；其中均值为E(x)=p，方差为Var(X)=p(1-p)
3.多项式朴素贝叶斯
Multinomial Naive Bayes是指当特征属性服从多项分布，从而，对于每个类别 y，参数为θy=(θy1,θy2,…,θyn)，其中n为特征属性数目，那么P(xi|y)的概率为θyi

三.实例

对于SNS社区来说，不真实账号（使用虚假身份或用户的小号）是一个普遍存在的问题，作为SNS社区的运营商，希望可以检测出这些不真实账号，从而在一些运营分析报告中避免这些账号的干扰，亦可以加强对SNS社区的了解与监管。

如果通过纯人工检测，需要耗费大量的人力，效率也十分低下，如能引入自动检测机制，必将大大提升工作效率。这个问题说白了，就是要将社区中所有账号在真实账号和不真实账号两个类别上进行分类，下面我们一步一步实现这个过程。

首先设C=0表示真实账号，C=1表示不真实账号。

1、确定特征属性及划分
三个特征属性：a1：日志数量/注册天数，a2：好友数量/注册天数，a3：是否使用真实头像。
下面给出划分：a1：{a<=0.05, 0.05=0.2}，a2：{a<=0.1, 0.1=0.8}，a3：{a=0（不是）,a=1（是）}。

2、获取训练样本
这里使用运维人员曾经人工检测过的1万个账号作为训练样本。

3、计算训练样本中每个类别的频率
P(C=0)=0.89
P(C=1)=0.11

4、计算每个类别条件下各个特征属性划分的频率
P(a1<=0.05|C=0)=0.3
P(0.05 P(a1>=0.2|C=0)=0.2
P(a1<=0.05|C=1)=0.8
P(0.05 P(a1>=0.2|C=1)=0.1

P(a2<=0.1|C=0)=0.1
P(0.1 P(a2>=0.8|C=0)=0.2
P(a2<=0.1|C=1)=0.7
P(0.1 P(a2>=0.8|C=1)=0.1

P(a3=0|C=0)=0.2
P(a3=1|C=0)=0.8
P(a3=0|C=1)=0.9
P(a3=1|C=1)=0.1

5、使用分类器进行鉴别
下面我们使用上面训练得到的分类器鉴别一个账号，这个账号使用非真实头像，日志数量与注册天数的比率为0.1，好友数与注册天数的比率为0.2。
a1=0.1,a2=0.2,a3=0
P(C=0)P(x|C=0)=P(C=0)P(0.050.50.7*0.2=0.0623

P(C=1)P(x|C=1)=P(C=1)P(0.050.10.2*0.9=0.00198

所以是真实的账号