自动驾驶路径规划——Dijkstra算法
目录
- 前言
- 1. 深度优先（DFS）和广度优先（BFS）
- 2. 深度优先搜索(DFS)
-
- 2.1 算法基本思想
- 2.2 深度优先搜索算法（C）
- 3. 广度优先搜索(BFS)
-
- 3.1 算法基本思想
- 3.2 广度优先搜索(BFS)（C）
- 4. Dijkstra算法
-
- 4.1 Dijkstra算法原理
- 4.2 Dijkstra算法基本步骤
- 5. MATLAB编写Dijkstra算法
-
- 5.1 defColormap.m
- 5.2 getNeighborNodes.m
- 5.3 Dijkstra.m
-
- S/U集的内容
- 5.4 实验效果
-
- Dijkstra 8邻域
- Dijkstra 4邻域
- 改进后的效果
- 平滑后的效果
- 运行时长
- 声明
前言
这个学期学校开设了相应的课程，同时也在学习古月居机器人学系列的《基于栅格地图的机器人路径规划指南》，为了巩固知识，方便自己的学习与整理，遂以学习笔记的形式记录。
1. 深度优先（DFS）和广度优先（BFS）
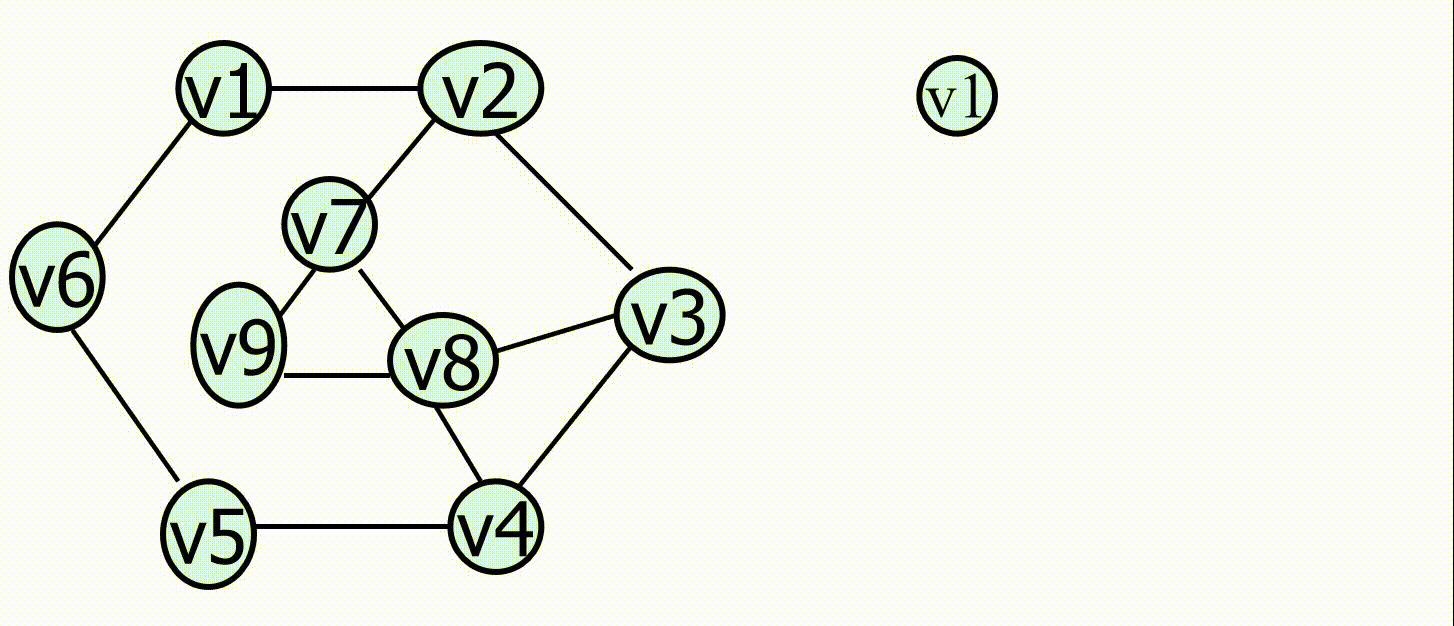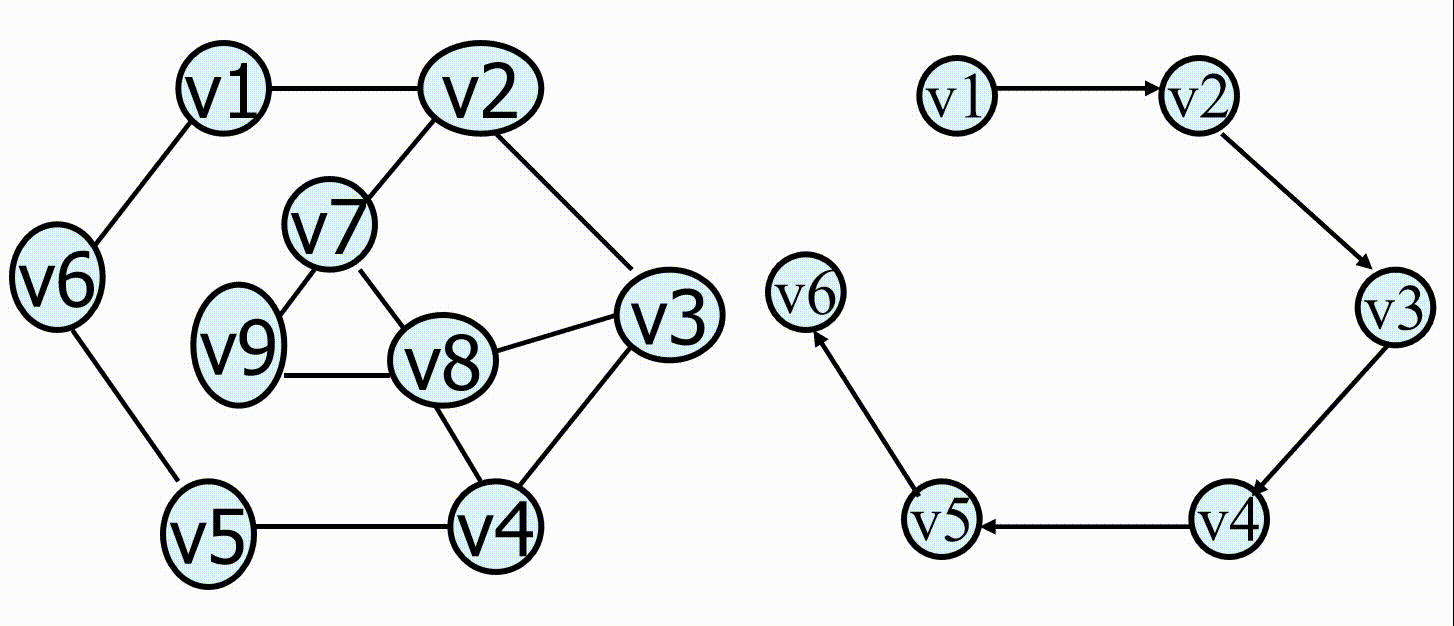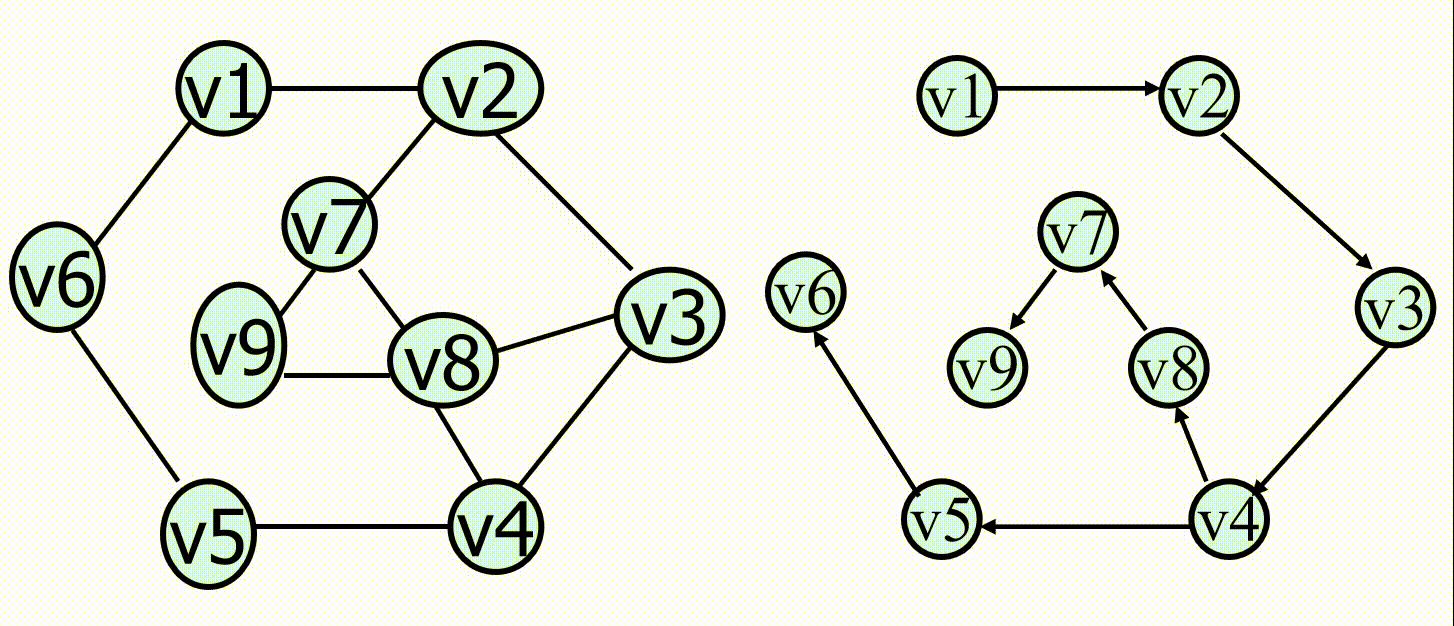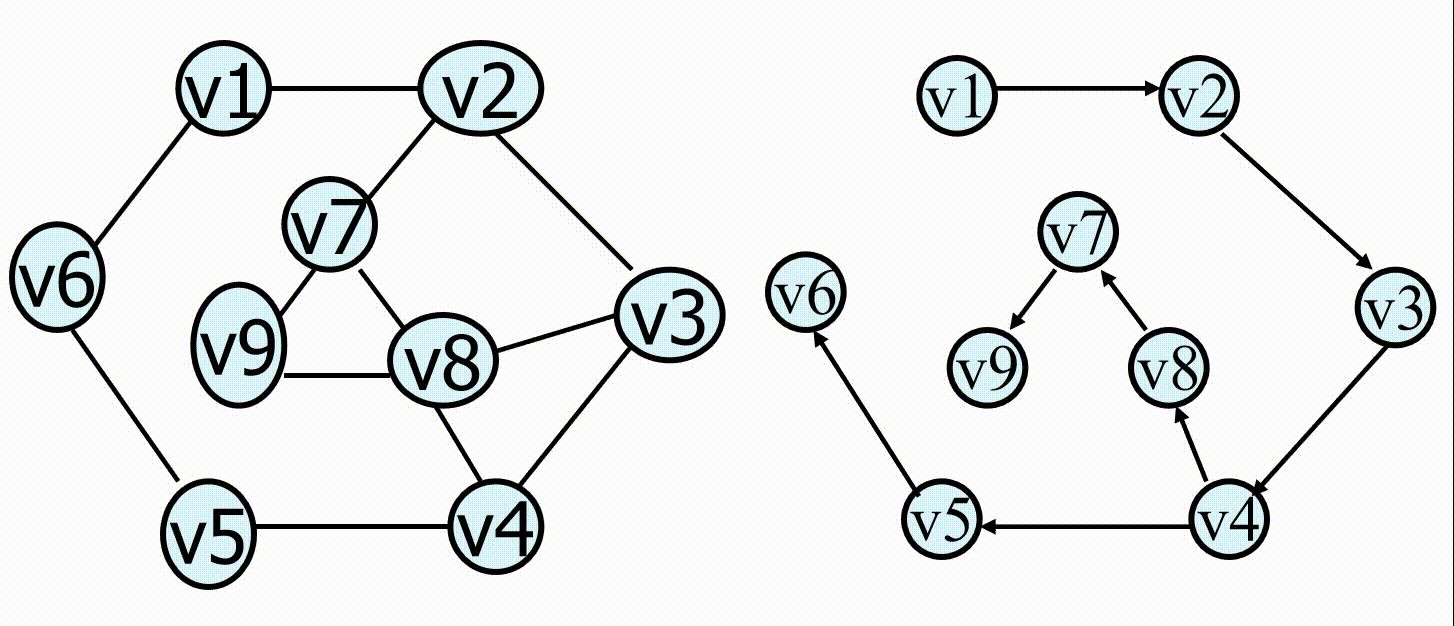
深度优先搜索（ Depth First Search , DFS )：首先从某个顶点出发，依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和该顶点有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
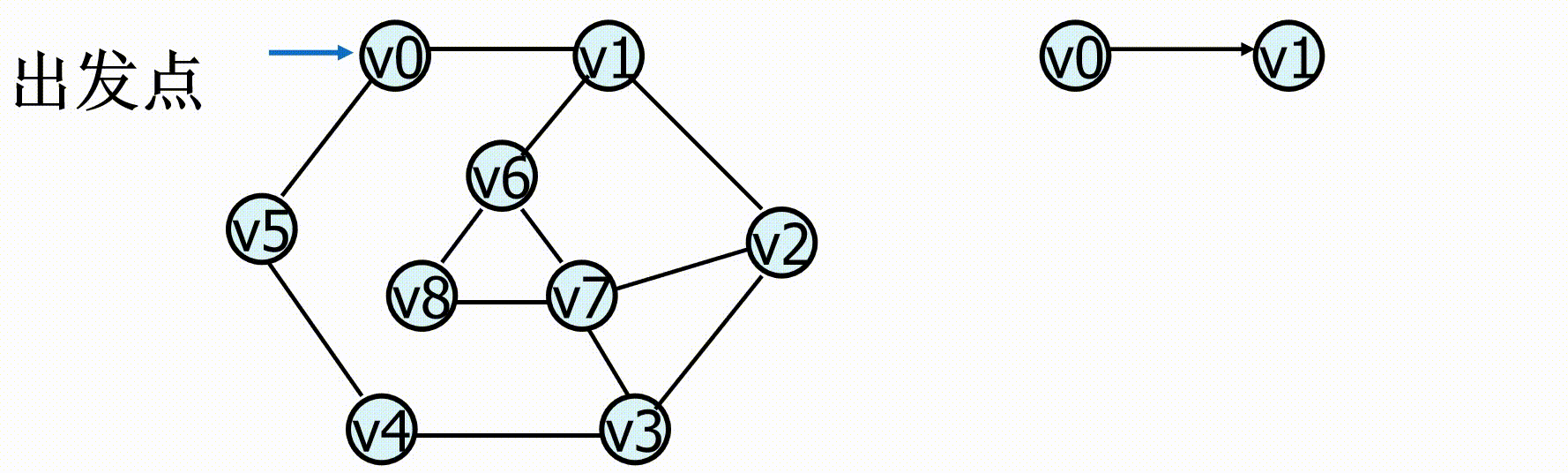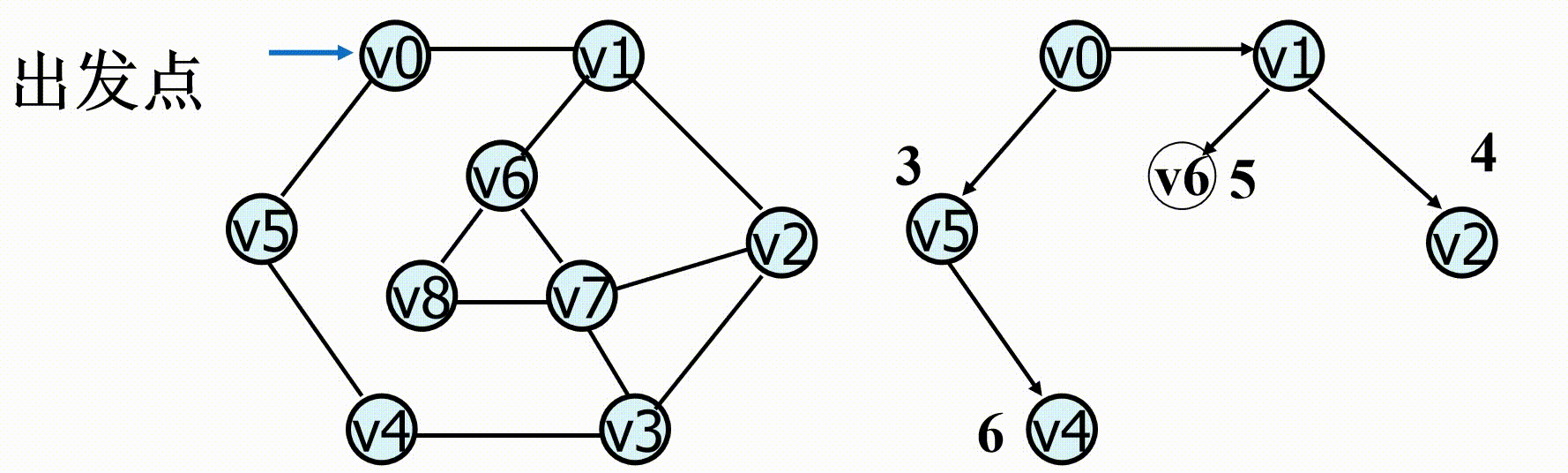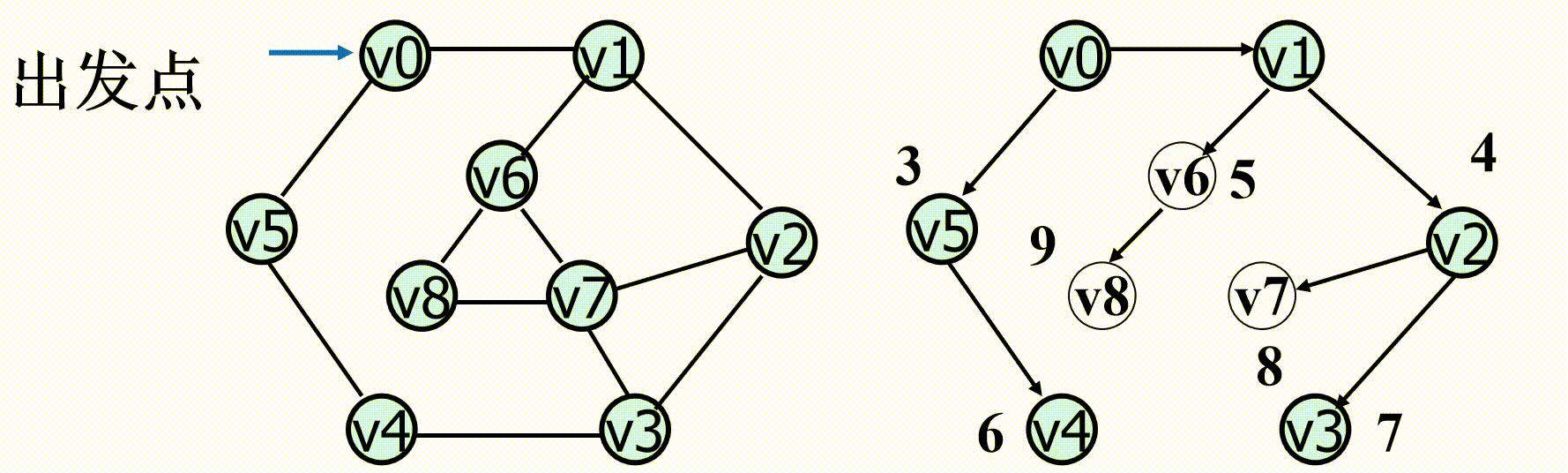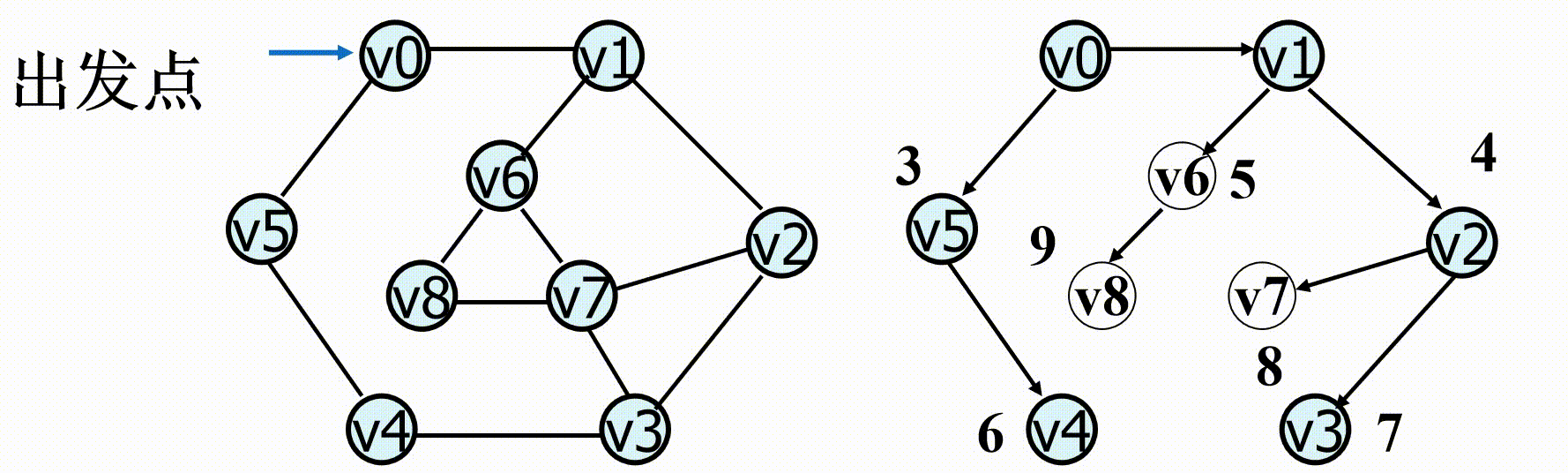
广度优先搜索（ Breadth First Search , BFS )：从图中某顶点出发，依次访问的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。
深度优先搜索和广度优先搜索分别类似于树的前序遍历和层次遍历。
Dijkstra 算法属于典型的广度优先搜索算法。
2. 深度优先搜索(DFS)
2.1 算法基本思想
- 首先访问图中某一个顶点Vi，以该顶点为出发点；
- 任选一与该顶点Vi邻接的未被访问的顶点Vj；访问Vj；
- 以Vj为新的出发点继续进行深度优先搜索，直至图中所有和Vi有路径的顶点被访问到。
2.2 深度优先搜索算法（C）
从图的某一点 v 出发，递归地进行深度优先遍历算法描述：
void DFSTraverse(Graph G)
{for (v=0; v<G.vexnum; ++v)
visited[v] = FALSE; /*访问标志数组初始化*/
for (v=0; v<G.vexnum; ++v)
if (!visited[v]) DFS(G, v); /*对尚未访问的顶点调用 DFS*/
}
void DFS(Graph G,int v ) /*从第 v 个顶点出发递归地深度优先遍历图 G*/
{ visited[v]=TRUE;Visit(v); /*访问第 v 个顶点*/
for(w=FisrtAdjVex(G,v);w>=0; w=NextAdjVex(G,v,w))
if (!visited[w]) DFS(G,w); /*对 v 的尚未访问的邻接顶点 w 递归调用 DFS*/
}
以邻接表为存储结构的整个图 G 进行深度优先遍历实现的 C 语言描述:
void DFSTraverseAL(ALGraph G) /*深度优先遍历以邻接表存储的图 G*/
{ int i;
for (i=0;i<G.vexnum;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G.vexnum;i++)
if (!visited[i]) DFSAL(G,i); /*vi未访问过，从 vi开始 DFS 搜索*/
}
void DFSAL(ALGraph G,int i) /*以 vi为出发点对邻接表存储的图 G 进行 DFS 搜索*/
{ ArcNode *p;
Visit(G.adjlist[i]); /*访问顶点 vi*/
visited[i]=TRUE; /*标记 vi已访问*/
p=G.adjlist[i].firstarc; /*取 vi边表的头指针*/
while(p) /*依次搜索 vi的邻接点 vj，j=p->adjvex*/
{ if (!visited[p->adjvex]) /*若 vj尚未访问，则以 vj为出发点向纵深搜索*/
DFSAL(G,p->adjvex);
p=p->nextarc; /*找 vi的下一个邻接点*/
} }
此部分详细原理解释可以参考严蔚敏的数据结构（C语言版）
遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间则取决于所采用的存储结构。当以邻接矩阵为图的存储结构时，查找每个顶点的邻接点所需时间为O(n2) ，其中 n 为图中顶点数。而当以邻接表作图的存储结构时，找邻接点所需时间为 O(e)，其中e 为无向图中边的数或有向图中弧的数。由此，当以邻接表作存储结构时，深度优先搜索遍历图的时间复杂度为 O(n+e) 。
3. 广度优先搜索(BFS)
3.1 算法基本思想
广度优先搜索（BFS）遍历类似于树的按层次遍历。
（1）首先访问图中某一指定的出发点Vi；
（2）然后依次访问VI的所有邻接点Vi1，Vi2……Vit；
（3）再依次以Vi1，Vi2……Vit为顶点，访问各顶点未被访问的邻接点，依此类推，直到图中所有顶点均被访问为止。
3.2 广度优先搜索(BFS)（C）
从图的某一点 v 出发，进行广度优先遍历算法描述：
void BFSTraverse (MGraph G) /*按广度优先非递归遍历图 G，使用辅助队列 Q*/
{
for (v=0; v<G.vexnum; ++v)
visited[i] = FALSE; /*访问标志数组初始化*/
for (v=0; v<G.vexnum; ++v)
if (!visited[v]) BFS(G, v); /*对尚未访问的顶点调用 BFS*/
}
void BFS (Graph G,int v) {InitQueue(Q); /*置空的辅助队列 Q*/
visited[v]=TRUE; Visit(v); /*访问 v*/
EnQueue(Q,v); /*v 入队列*/
while (!QueueEmpty(Q))
{ DeQueue(Q,u); /*队头元素出队并置为 u*/
for(w=FistAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w))
if(!visited[w])
{visited[w]=TRUE; Visit(w);
EnQueue(Q,w); /*u 尚未访问的邻接顶点 w 入队列 Q*/
}
}
}
以邻接矩阵为存储结构的整个图 G 进行广度优先遍历实现的 C 语言描述。
void BFSTraverseAL(MGraph G) /*广度优先遍历以邻接矩阵存储的图 G*/
{
int i;
for (i=0;i<G.vexnum;i++)
visited[i]=FALSE; /*标志向量初始化*/
for (i=0;i<G.vexnum;i++)
if (!visited[i]) BFSM(G,i); /* vi未访问过，从 vi开始 BFS 搜索*/
}
void BFSM(MGraph G,int k) /*以 vi为出发点，对邻接矩阵存储的图 G 进行 BFS 搜索*/
{
int i,j;
sqQueue Q;
InitQueue(Q);
Visit(G.vexs[k]); /*访问原点 Vk*/
visited[k]=TRUE;
EnQueue(Q,k); /*原点 Vk入队列*/
while (!QueueEmpty(Q))
{i=DeQueue(Q); /*Vi出队列*/
for (j=0;j<G.vexnum;j++) /*依次搜索 Vi的邻接点 Vj*/
if(G.edges[i][j]==1 && !visited[j]) /*若 Vj未访问*/
{Visit (G.vexs[j]); /*访问 Vj */
visited[j]=TRUE;
EnQueue(Q,j); /*访问过的 Vj入队列*/
}
}
}
此部分详细原理解释可以参考严蔚敏的数据结构（C语言版）
4. Dijkstra算法
Dijkstra 算法是由荷兰计算机科学家迪杰斯特拉于1959年提出的，是从一个节点遍历其余各节点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
4.1 Dijkstra算法原理
初始点看作一个集合S，其它点看作另一个集合挨个的把离初始点最近的点找到并加入集合S，集合中所有的点的d[i]都是该点到初始点最短路径长度，由于后加入的点是根据集合S中的点为基础拓展的，所以能找到最短路径。
用途： 用于求图中指定两点之间的最短路径，或者是指定一点到其它所有点之间的最短路径。
4.2 Dijkstra算法基本步骤
- 将图上的初始点看作一个集合S，其它点看作另一个集合
- 根据初始点，求出其它点到初始点的距离d[i] （若相邻，则d[i]为边权值；若不相邻，则d[i]为无限大）
- 选取最小的d[i]（记为d[x]），并将此d[i]边对应的点（记为x）加入集合S（实际上，加入集合的这个点的d[x]值就是它到初始点的最短距离）
- 再根据x，更新跟 x 相邻点 y 的d[y]值：d[y] = min{ d[y], d[x] + 边权值w[x][y] }，因为可能把距离调小，所以这个更新操作叫做松弛操作。
- 重复3，4两步，直到目标点也加入了集合，此时目标点所对应的d[i]即为最短路径长度。（注：重复第三步的时候，应该从所有的d[i]中寻找最小值，而不是只从与x点相邻的点中寻找）
图片中 B（23） 应该是B（13）
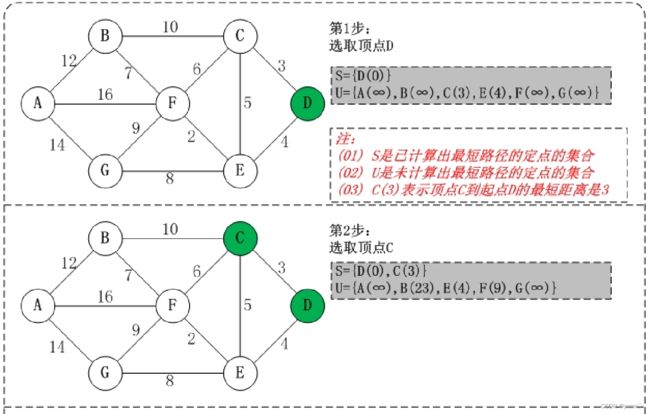
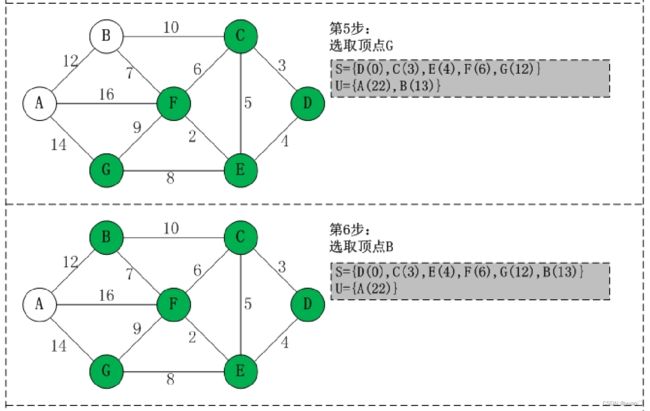
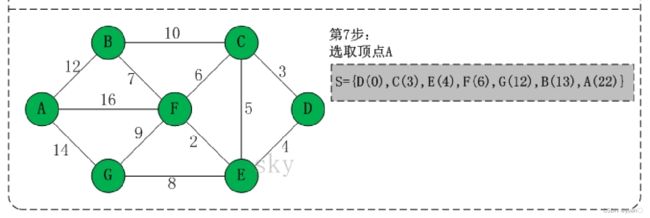
Dijkstra 算法十分简洁，能够有效的找到最优解，不足之处在数据节点庞大时所需的节点繁多，效率随着数据节点的增加而下降，耗费大量内存空间与计算时间。
5. MATLAB编写Dijkstra算法
MATLAB 编写 Dijkstra 算法的几个核心要素：
- 可以考虑将第1讲的栅格地图场景定义单独存为一个函数，无需出现在算法的主程序里。
- 前面的案例基于拓扑地图展开叙述，那么对于栅格地图，通常采用8邻域。考虑到“遍历每一个节点的邻近节点”的功能在程序中会多次出现，故可以考虑将其单独存为一个函数，以便调用。
5.1 defColormap.m
可以将之前所创建的栅格地图作为一个函数来使用
详见——路径规划——基于MATLAB的栅格地图
function [field,cmap] = defColorMap(rows, cols)
cmap = [1 1 1; ... % 1-白色-空地
0 0 0; ... % 2-黑色-静态障碍
1 0 0; ... % 3-红色-动态障碍
1 1 0;... % 4-黄色-起始点
1 0 1;... % 5-品红-目标点
0 1 0; ... % 6-绿色-到目标点的规划路径
0 1 1]; % 7-青色-动态规划的路径
% 构建颜色MAP图
colormap(cmap);
% 定义栅格地图全域，并初始化空白区域
field = ones(rows, cols);
% 障碍物区域
obsRate = 0.2;
obsNum = floor(rows*cols*obsRate);
obsIndex = randi([1,rows*cols],obsNum,1);
field(obsIndex) = 2;
5.2 getNeighborNodes.m
function neighborNodes = getNeighborNodes(rows, cols, lineIndex, field)
[row, col] = ind2sub([rows,cols], lineIndex);
% neighborNodes = inf(4,2);
neighborNodes = inf(8,2);
%% 查找当前父节点临近的周围8个子节点 注释掉后为4邻域
% 左上节点
if row-1 > 0 && col-1 > 0
child_node_sub = [row-1, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
child_brother_node_sub1 = [row-1, col];
child_brother_node_sub2 = [row, col-1];
neighborNodes(1,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
if ~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2)
cost = norm(child_node_sub - [row, col]); % 欧式距离，计算出代价
neighborNodes(1,2) = cost;
end
end
end
% 上节点
if row-1 > 0
child_node_sub = [row-1, col];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(2,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(2,2) = cost;
end
end
% 右上节点
if row-1 > 0 && col+1 <= cols
child_node_sub = [row-1, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
child_brother_node_sub1 = [row-1, col];
child_brother_node_sub2 = [row, col+1];
neighborNodes(3,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
if ~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2)
cost = norm(child_node_sub - [row, col]);
neighborNodes(3,2) = cost;
end
end
end
% 左节点
if col-1 > 0
child_node_sub = [row, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(4,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(4,2) = cost;
end
end
% 右节点
if col+1 <= cols
child_node_sub = [row, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(5,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(5,2) = cost;
end
end
% 左下节点
if row+1 <= rows && col-1 > 0
child_node_sub = [row+1, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
child_brother_node_sub1 = [row, col-1];
child_brother_node_sub2 = [row+1, col];
neighborNodes(6,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
if ~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2)
cost = norm(child_node_sub - [row, col]);
neighborNodes(6,2) = cost;
end
end
end
% 7.下节点
if row+1 <= rows
child_node_sub = [row+1, col];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(7,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(7,2) = cost;
end
end
% 8.右下节点
if row+1 <= rows && col+1 <= cols
child_node_sub = [row+1, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
child_brother_node_sub1 = [row, col+1];
child_brother_node_sub2 = [row+1, col];
neighborNodes(8,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
if ~(field(child_brother_node_sub1(1), child_brother_node_sub1(2)) == 2 & field(child_brother_node_sub2(1), child_brother_node_sub2(2)) == 2)
cost = norm(child_node_sub - [row, col]);
neighborNodes(8,2) = cost;
end
end
end
5.3 Dijkstra.m
% 基于栅格地图的机器人路径规划算法
% 第2节：Dijkstra算法
clc
clear
close all
%% 栅格界面、场景定义
% 行数和列数
rows = 20;
cols = 20;
[field,cmap] = defColorMap(rows, cols);
% 起点、终点、障碍物区域
startPos = 2;
goalPos = rows*cols -1 ;
field(startPos) = 4;
field(goalPos) = 5;
%% 算法初始化
% S/U的第一列表示栅格节点线性索引编号
% 对于S，第二列表示从源节点到本节点已求得的最小距离，不再变更；
% 对于U，第二列表示从源节点到本节点暂时求得的最小距离，可能会变更
U(:,1) = (1: rows*cols)';
U(:,2) = inf;
S = [startPos, 0];
U(startPos,:) = [];
% 更新起点的邻节点及代价
neighborNodes = getNeighborNodes(rows, cols, startPos, field);
% for i = 1:4
for i = 1: 8
childNode = neighborNodes(i,1);
% 判断该子节点是否存在
if ~isinf(childNode)
idx = find(U(:,1) == childNode);
U(idx,2) = neighborNodes(i,2);
end
end
% S集合的最优路径集合
for i = 1:rows*cols
path{i,1} = i;
end
% for i = 1:4
for i = 1: 8
childNode = neighborNodes(i,1);
if ~isinf(neighborNodes(i,2))
path{childNode,2} = [startPos,neighborNodes(i,1)];
end
end
%% 循环遍历
while ~isempty(U)
% 在U集合找出当前最小距离值的节点,视为父节点，并移除该节点至S集合中
[dist_min, idx] = min(U(:,2));
parentNode = U(idx, 1);
S(end+1,:) = [parentNode, dist_min];
U(idx,:) = [];
% 获得当前节点的临近子节点
neighborNodes = getNeighborNodes(rows, cols, parentNode, field);
% 依次遍历邻近子节点，判断是否在U集合中更新邻节点的距离值
% for i = 1:4
for i = 1: 8
% 需要判断的子节点
childNode = neighborNodes(i,1);
cost = neighborNodes(i,2);
if ~isinf(childNode) && ~ismember(childNode, S)
% 找出U集合中节点childNode的索引值
idx_U = find(childNode == U(:,1));
% 判断是否更新
if dist_min + cost < U(idx_U, 2)
U(idx_U, 2) = dist_min + cost;
% 更新最优路径
path{childNode, 2} = [path{parentNode, 2}, childNode];
end
end
end
end
%% 画栅格界面
% 找出目标最优路径
path_opt = path{goalPos,2};
% 给所有访问过的节点上色
for i = 1:rows*cols
if ~isempty(path{i,2})
field((path{i,1})) = 7;
end
end
field(startPos) = 4;
field(goalPos) = 5;
field(path_opt(2:end-1)) = 6;
% 画栅格图
image(1.5,1.5,field);
grid on;
set(gca,'gridline','-','gridcolor','k','linewidth',2,'GridAlpha',0.5);
set(gca,'xtick',1:cols+1,'ytick',1:rows+1);
axis image;
hold on;
% 画出轨迹
[y0,x0] = ind2sub([rows,cols], path_opt);
y = y0 + 0.5;
x = x0 + 0.5;
plot(x,y,'-','Color','r','LineWidth',2.5);
hold on;
% 对轨迹进行平滑——贝塞尔曲线
points = [x',y'];
M = 1000;
[x1,y1] = bezir_n(points, M);
plot(x1,y1,'-','Color','y','LineWidth',2.5);
% 对轨迹进行平滑——spcrv
hold on;
values = spcrv([[x(1) x x(end)];[y(1) y y(end)]],3);
plot(values(1,:),values(2,:), 'b','LineWidth',2.5);
S/U集的内容
| 第一列索引值 | 第二列索引值(代价值——距离) | 代表含义 |
|---|---|---|
| lnf | lnf | 未遍历 |
| number | lnf | 障碍物 |
| number | number | 空地 |
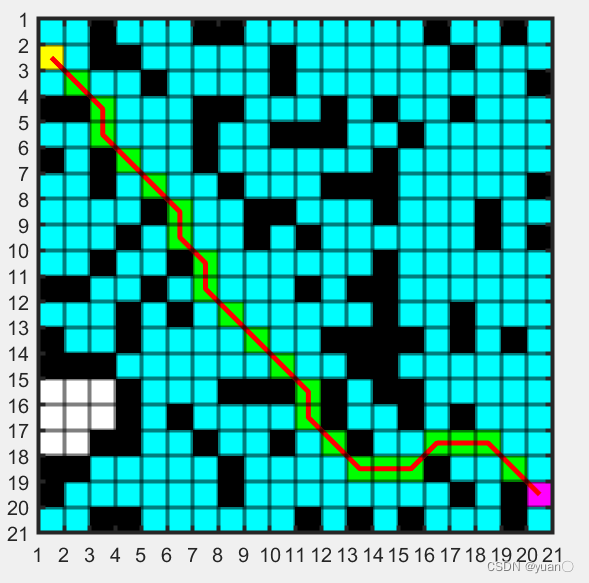
5.4 实验效果
Dijkstra 8邻域
注： 黄色——起点
紫色——终点
白色——空地
黑色——障碍物
绿色——最终路径
可以看到，Dijkstra算法几乎将所有能访问的点都访问了，其运算量较大，但同时能够得到最优解。
Dijkstra 4邻域
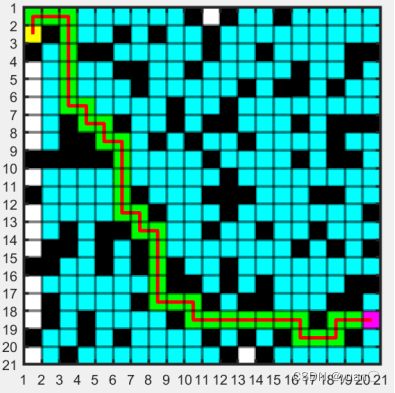
4邻域走的路径大多是直角，相比8邻域，不太平滑。
如下图所示：8邻域会出现这样一种状况。显然在现实中这种走法会与障碍相碰撞。对此，需要进行相关约束。例如，当要走左下方向时，还需要保证其左节点和下节点不为障碍物。
改进后的效果
可以看到不会再出现上述问题。但仍有一个缺陷——在部分转角时，会发生转向过大的问题，这对实际的无人车控制显然是不太合理的，对此采用贝塞尔曲线进行平滑。
平滑后的效果
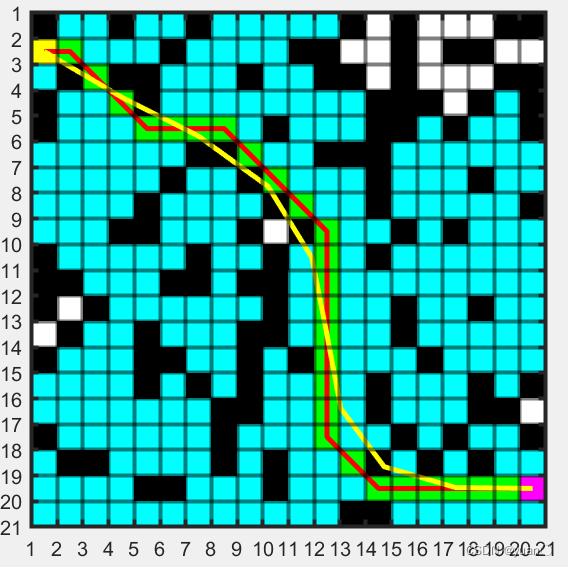
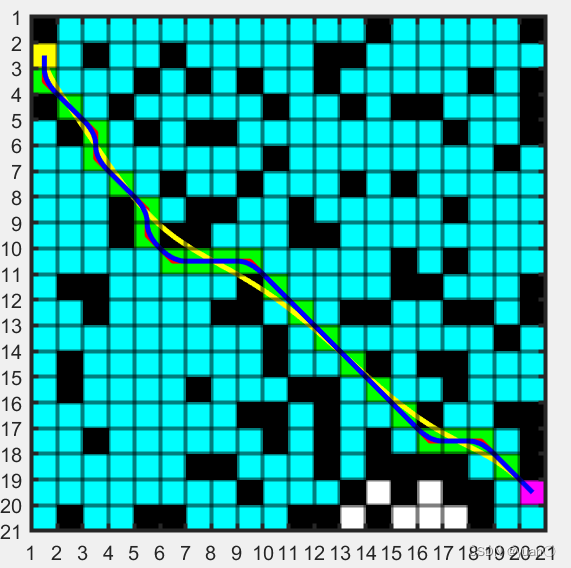
红色为未平滑路径，绿色方块为最终路径，黄色为贝塞尔曲线拟合得到，蓝色为spcrv函数平滑得到。
运行时长
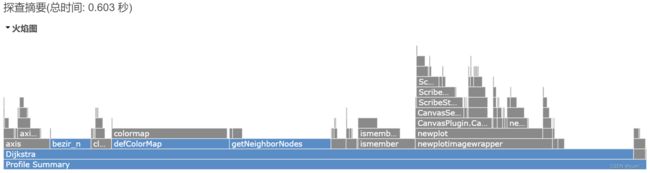栅格地图大小（20x20）
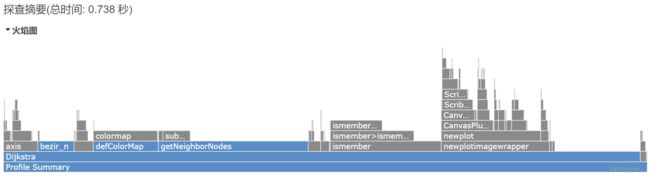栅格地图大小（30x30）
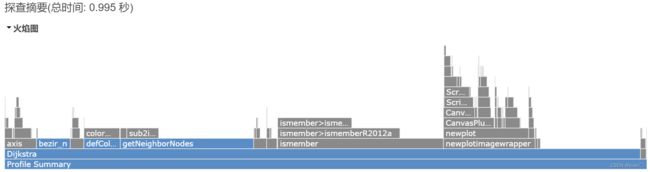
栅格地图大小（40x40）
可以看到Dijkstra算法对于栅格地图越大的情况，搜索时间越长，但其总耗时较长，不适用于实时的路径规划，不适用于局部路径规划，适用于全局路径规划。
声明
本人所有文章仅作为自己的学习记录，若有侵权，联系立删。