PyTorch深度学习实践概论笔记6-逻辑斯蒂回归
上一讲PyTorch深度学习实践概论笔记5-用pytorch实现线性回归介绍了用pytorch实现线性回归。这一讲主要讨论机器学习任务中的分类问题。我们要介绍的模型是Linear Regression,虽然名字叫回归,但是是处理分类问题。
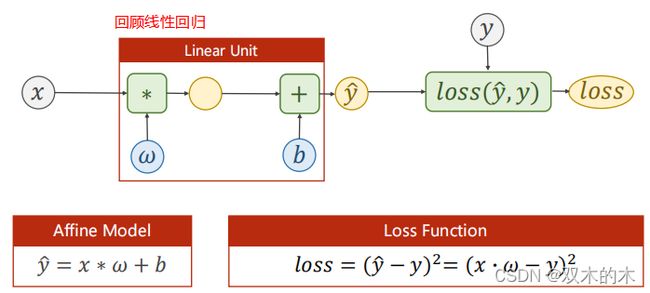
0 Revision-Linear Regression
回顾上一讲使用的数据,y是属于连续空间的,处理这种类型的数据一般用回归。但是在很多机器学习任务中要做的是分类。
1 Classification introduction
1.1 Classification-The MNIST Dataset
MNIST 数据集来自美国国家标准与技术研究所,National Institute of Standards and Technology (NIST)。 一共提供70000个样本。训练集 (training set) 由来自 250 个不同人手写的数字构成,其中 50% 是高中学生,50% 来自人口普查局 (the Census Bureau) 的工作人员。测试集(test set) 也是同样比例的手写数字数据。
因此y是属于一个离散值的集合{0,1,2,3,4,5,6,7,8,9},需要预测y是属于其中哪一个,这是分类问题。如果用回归做分类问题,是不合理的,因为类别之间没有实数当中数值大小的含义。在分类问题里面输出的是概率,找到概率最大的分类。在torchvision中有这个数据集,可以通过下面代码获取:
import torchvision
train_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=True, download=True)
test_set = torchvision.datasets.MNIST(root='../dataset/mnist', train=False, download=True)1.2 Classification-The CIFAR-10 Dataset
CIFAR-10是一个更接近普适物体的彩色图像数据集。CIFAR-10 是由Hinton 的学生Alex Krizhevsky 和Ilya Sutskever 整理的一个用于识别普适物体的小型数据集。一共包含10 个类别的RGB 彩色图片:飞机( airplane )、汽车( automobile )、鸟类( bird )、猫( cat )、鹿( deer )、狗( dog )、蛙类( frog )、马( horse )、船( ship )和卡车( truck )。每个图片的尺寸为32 × 32 ,每个类别有6000个图像,数据集中一共有50000 张训练图片和10000 张测试图片。在torchvision中也有这个数据集,可以通过下面代码获取:
import torchvision
train_set = torchvision.datasets.CIFAR10(…)
test_set = torchvision.datasets.CIFAR10(…)MNIST 数据集和CIFAR-10数据集对比:
(1) MNIST 是灰度图像,而CIFAR-10 是3通道(RGB)的彩色图像。
(2) MNIST 的图片尺寸为28 × 28,而CIFAR-10 的图片尺寸为32 × 32 。
(3) 相比于手写字符, CIFAR-10 含有的是现实世界中真实的物体,不仅噪声很大,而且物体的比例、特征都不尽相同,这为识别带来很大困难。直接的线性模型如Softmax 在CIFAR-10 上表现得很差。
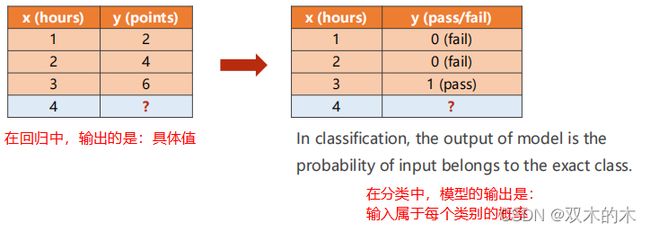
1.3 Regression vs Classification
只有两个类别的分类称为二分类,例如,pass或fail。在回归中,模型输出的是具体值;在分类中,模型输出的是输入x属于每个类别的概率,一般取概率最大的类。
2 Classification
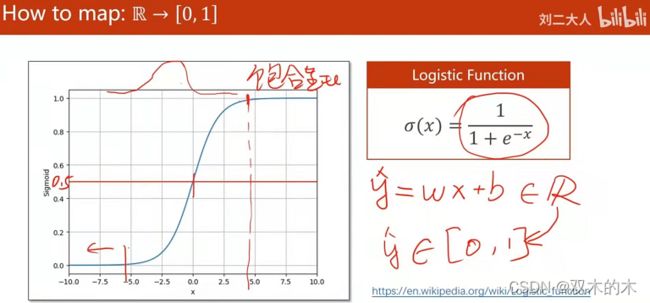
2.1 How to map?
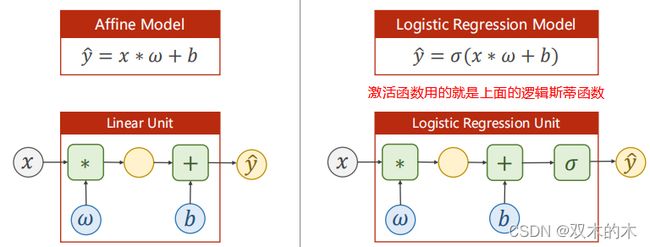
如何把输出从实数空间R映射到[0,1]区间呢?引入逻辑斯蒂函数。
计算得到的y=w*x+b代入逻辑斯蒂函数,控制y hat的取值在0-1。
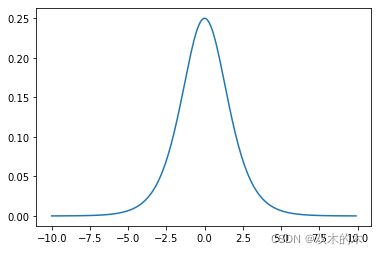
导函数类似上图这种形状的函数称为饱和函数。这个函数和正态分布有关系,具体可以查看链接拓展阅读。这种映射处理也保证了输出的概率在0-1之间。
2.2 Sigmoid functions
在做分类时可以用线性模型,再把输出用sigmoid函数算一下。看看其他的sigmiod函数。
如上图所示,这些都叫sigmoid函数,满足函数值有极限,函数值在(-1,1)之间,都是单调增函数,都是饱和函数,满足这几个条件就叫sigmoid函数。在所有的sigmoid函数中逻辑斯蒂函数最出名,所以现在有些框架里面就直接把逻辑斯蒂函数叫做sigmoid函数,在pytorch里面逻辑斯蒂函数就叫做sigmoid函数。
2.3 Logistic regression model
上面的sigma就是逻辑斯蒂函数。
2.4 Loss function for binary classification
请注意,模型变了之后,loss函数也跟着改变。
linear regression的y hat减y是实数相减,现在分类不再是数值,而是分布,y hat=P(class=1)和y=P(class=0) ,现在衡量的是分布之间的差异。(在概率论与数理统计中有KL散度)在这里的二分类中用的是cross-entropy(交叉熵)。
上述公式计算的loss就是BCE损失。如上表,当预测值越接近真实值,BCE损失越小,预测结果越准。对于多个样本的情况,计算Mini-Batch loss时取均值。
2.5 Implementation of Logistic Regression
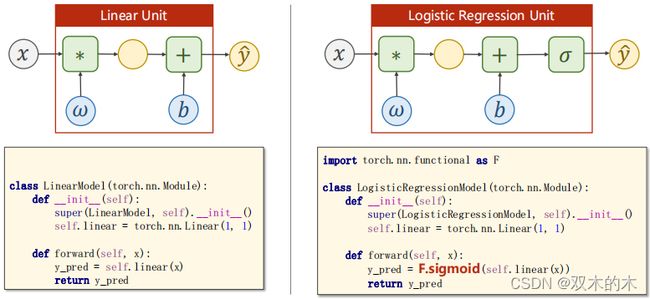
看看一般的线性回归模型和逻辑斯蒂回归模型的代码对比:
线性回归模型代码:
class LinearModel(torch.nn.Module):
def __init__(self):
super(LinearModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred逻辑斯蒂回归模型代码:
import torch.nn.functional as F
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = F.sigmoid(self.linear(x))
return y_pred看看整体训练过程,跟线性回归类似:
基于pytorch,整个的深度学习框架基本上都分成以上的4部分。之后也可以相应的加一些内容。
代码分析:
#1.准备数据集
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
#-------------------------------------------------------#
#2.设计模型
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)#linear是由Linear实例化得到的
def forward(self, x):
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
#-------------------------------------------------------#
#3.构造损失函数和优化器
criterion = torch.nn.BCELoss(size_average=False)
#size_average=False表示得到的损失不求均值
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#优化器不会构建计算图 torch.optim.SGD是一个类,带了参数就是实例化了这个类
#model.parameters()获得model的相应权重
#lr是学习率
#-------------------------------------------------------#
#4.训练
for epoch in range(1000):
y_pred = model(x_data)#通过前向传播算出y_pred
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()2.6 Result of Logistic Regression
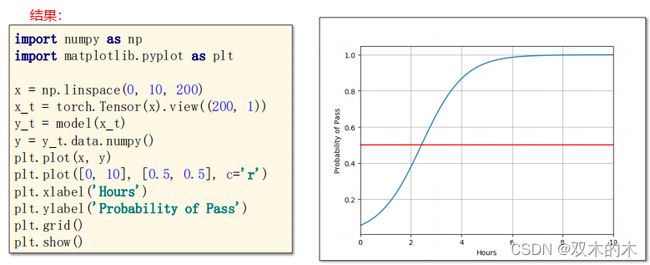
在上述训练完成之后,可以用得到的模型进行测试。
代码分析:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1)) #类似于np的reshape
y_t = model(x_t) #进行测试
y = y_t.data.numpy()
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()这一讲没有练习。
说明:记录学习笔记,如果错误欢迎指正!写文章不易,转载请联系我。