利用公共子图同构计算图编辑距离相似度（CSI_GED:An Efficient Approach for Graph Edit Similarity Computation ICDE2016）

文章介绍：

1. 文章标题：CSI_GED:An Efficient Approach for Graph Edit Similarity Computation
2. 文章来源：ICDE 2016
3. 作者单位：
   单位：埃及-本哈大学计算机与信息学院
   作者：卡拉姆·古达(经常研究图相似度搜索)
4. 原文链接
5. 百度文库链接

图1

摘要

 图相似度是许多应用程序中的基本操作。在本文中，我们主要讨论基于编辑距离的图相似度计算。现有的图编辑距离计算方法采用最佳优先的A * 搜索算法。这些方法受时间和空间限制。实际上，A* 算法只可以计算最多包含12个顶点的图的编辑距离。为了在较大和较远的图上实现图编辑相似性计算，我们提出了CSI_GED，这是一种新颖的基于边的映射方法，用于通过常见子结构同构枚举来计算图编辑距离。CSI_GED将回溯搜索与许多启发式技术结合使用，以减少内存需求并快速减少大部分映射搜索空间。实验表明，CSI_GED在计算小图，大图和编辑距离比较远的图上的编辑距离都非常有效。此外，我们将CSI_GED评估为独立的图编辑相似性搜索查询方法。实验表明，CSI_GED是有效且可扩展的，并且比基于最新索引的方法要高出两个数量级。

原文链接

文章简介

发表于：2016 IEEE第32届国际数据工程会议（ICDE）

第一节 介绍

  当前，大规模图形数据在诸如模式识别，生物信息学，化学信息学，社交网络，语义网，软件工程等领域中很普遍。由于图形模型的广泛应用，最近已经投入了大量的研究工作。在管理和分析图形数据时遇到的各种问题。
  计算图形对象的相似度是许多应用中的基本且必不可少的操作，包括图形分类和聚类[1]，[2]，化学中的分子比较[3]，计算机视觉中的对象识别[4]，图形相似性搜索和连接[5] – [6] [7] [8]等等。在本文中，我们讨论基于编辑距离的图相似度计算。与其他距离或相似性度量相比，图形编辑距离（GED）作为相似性度量更为可取，因为它具有公共性和广泛的适用性。它几乎适用于所有类型的数据图，其节点和边的标签字母不受限制，并且可以精确捕获结构差异。更有趣的是，随附的编辑序列为编辑距离值提供了解释，这对用户来说是非常有价值的功能。

  不幸的是，图编辑距离的吸引人的特性是以高计算复杂性为代价的。计算图形编辑距离已知是NP难题[6]。与其他难以解决的图匹配问题（例如，子图同构和最大公共子图同构）不同，为了计算图编辑距离，一个图的顶点可以映射到另一图的任何顶点，而不管它们的标签和度数如何。因此，搜索空间相对于所涉及图的顶点数是指数的。

  为解决图形编辑距离计算的高复杂性，目前(2016年)仅进行了很少的工作。大多数现有方法[9] – [10] [11] [12] 都采用最有限搜索策略A∗ 。A∗基本思想就是要找到从一个图的顶点到另一个图的顶点的映射，这会推算出最低的编辑成本。为了达到目标，A∗使用诸如遍历有序树一样的方法探索潜在的顶点映射空间，其中中间树节点代表局部（partial）映射，叶节点代表完整（complete）映射。在每一次的搜索状态下，A* 选择最佳的局部映射进行扩展，在这些拓展的时候，这些映射是当前具有最小induced编辑成本。继续此过程，直到选定的映射是一个完整的。

   A* 算法的方法主要问题是，局部映射的数量变得非常大，尤其是在比较大图和编辑距离比较远的图时。这些映射大多数都不能丢弃，必须一直维护到搜索的最后阶段，结果需要巨大的内存。另一个瓶颈是选择最小成本的局部映射以及为每个可能的映射扩展更新该成本所需的昂贵计算。内存和计算开销使A*算法的方法无法计算具有12个以上顶点的图形的编辑距离。实际上，较大的图并不少见。考虑例如药物开发领域。为了研究新化合物的性质，药物设计人员首先向化合物数据库查询与新化合物具有相似性编辑阈值的那些化合物。此步骤称为化合物筛选[13]，因为相似的化合物可能具有相似的生物活性，因此可以帮助药物设计者初步了解化合物。化学化合物数据库包含的图的平均顺序（average order）至少是A ∗可以处理的顺序的两倍。

  在本文中，我们提出了一种用于图编辑距离计算的新颖方法，称为CSI_GED，它可以最小化内存需求，并缩放到更大和更远的图。CSI_GED使用完全不同的方法来获取编辑距离。CSI_GED会先映射边，然后再直接从其最终顶点上计算编辑成本，而不是先映射顶点，然后再推断出边的编辑成本。虽然边的映射空间看起来相对较大，但是也只有在其组成顶点与先前匹配的顶点一致时才允许边匹配，这种匹配方法称为公共子结构同构限制。这种限制大大减少了搜索空间。此外，计算部分边映射所推断出的编辑距离很容易计算，因为它是直接从导出的公共子结构中计算出来的。相反， A* 的方法相当昂贵，因为针对每个可能的映射扩展倒要在单独的阶段中完成。

  CSI_GED利用回溯来探索边映射空间。最重要的好处是，对A* 算法是一个很重的负担的内存开销，将会被大大减小，因为 A* 使用深度优先，枚举了边的映射。此外，CSI_GED的框架允许实施多种启发式方法，以快速修剪掉大部分毫无希望的公共子结构同构。这些启发式方法是基于以下事实而开发的：先前已经探索完图的编辑成本是图编辑距离上的有效上限（即到目前为止在搜索中看到的）。因此，这些启发式方法的主要目标是强制执行搜索状态，这些状态相应的编辑成本超过了要先前遇到的最小上限值。¹

  因此节省了很大的空间。为了实现这一目标，第一个启发式方法是能够快速找到更严格的上界，而第二个最大化分配给每个映射的初始成本。文章最后的启发式搜索实现了搜索的预测(look-head)功能。

  实验表明，CSI_GED在计算小图，大图和编辑距离比较远的图上的编辑距离都非常有效。此外，我们将CSI_GED评估为独立²

的图编辑相似性搜索查询方法。实验表明，CSI_GED是有效且可扩展的，并且比基于最新索引的方法要高出两个数量级。

 本文的其余部分安排如下。

1. 在第2部分介绍图编辑相似度计算和最新针对此问题的方法。
2. 第3部分介绍了CSI_GED的框架及其构建的原因。
3. 第4节提出了用于优化CSI_GED不同试探法。
4. 在第5节CSI_GED在图形编辑相似性搜索问题的应用。
5. 在第6节分析实验结果报告。
6. 第7节讨论了相关工作。
7. 第8节总结全文。

第二节 前言

A.问题定义

  图 G 被定义为点对$(V,E)$的集合，其中$V=\{v_1,v_2,v_3,...,v_{|V|}\}$是一组顶点，并且$E\subseteq V\times V$是一组边（有向或无向）。 $|V|$和$|E|$ 是G顶点和边的数量，以及同时分别称为G的顺序（order）和大小(size)。给定一组离散值标签Σ，带标签的图 G 是三元组$（V，E，l）$，期中 $l$是标签函数：V∪ E→ Σ。让$L_V$ 和$L_E$ 表示分配给G的顶点和边的标签。本文着重于研究简单（无自环，无重复边），无向和标记图。在下面的描述中，标记图G的未标记版本，即G的结构，称为$S(G)$，除非另有说明，否则带标签的图简称为图。
  如果图$G$和另外一个图$G^{{}^{\prime }}$存在包含关系，用$G⊑G^{{}^{\prime }}$表示，则称图$G$是图$G^{{}^{\prime }}$的子图，或者图$G^{{}^{\prime }}$是图$G$的超图。

定义1：（子）图同构

  如果俩个图$G$和$G^{{}^{\prime }}$之间存在以下条件，则称俩个图是同构的：存在一个单射函数$f$，

使得

$(1){\forall }_{u\in V},l(u)=l^{{}^{\prime }}(f(u))$
$(2){\forall }_{(u,v)\in E},(f(u,v)\in E^{{}^{\prime }}),且l((u,v))=l^{{}^{\prime }}((f(u),f(v)).$

如果$G⊑G^{{}^{\prime }},并且G^{{}^{\prime }}⊑G$，则俩个图是同构的，用$G\cong G^{{}^{\prime }}$表示。
  图编辑操作[14]是对图进行的将其转换为另一图的操作。编辑操作包括插入或删除顶点或边，或更改顶点或边标签（称为重新标记）。给定两个图形$G_1$和$G_2$，对其中一个进行操作以获取另一个的顺序称为编辑路径。如果用数学记号则表示如下，令$p_i$为编辑操作，编辑路径$P=⟨p_i{⟩}_{i=1}^k$是将$G_1$转换为$G_2$的一系列编辑操作$⟨p_1，p_2，\dots ，p_k⟩$，即$P(G_1)=G_1{\to }^{p_1}{G}^1{\to }^{p_2}{G}^2\dots {\to }^{p_k}{G}^k\cong G_2$。使用$P$将$G_1$转换为$G_2$的编辑成本定义为：$C(G^1，G^2，P)={\sum }_{i=1}^{k}c(p_i)$，其中$c(p_i）$是单个编辑操作$p_i$的成本。取每个编辑操作的单位成本，即$c(p_i)=1$，$\forall i$，最小长度的编辑路径称为最佳编辑路径。

定义2：图形编辑距离

  给定两个图$G_1$和$G_2$。$G_1$和$G_2$之间的编辑距离，表示为$GED(G_1，G_2)$，是将$G_1$转换为$G_2$的最佳编辑路径的长度。

  以下是GED的两个简单但有效的下限，我们将在本文中使用它们。它们被称为全局（标签）边界。第一个是根据比较图的大小(顶点个数)和顺序（边个数）的差异得出的，由[6]给出为：
$$GED（G_1，G_2）\ge \Vert V_1|-|V_2\Vert +\Vert E_1|-|E_2\Vert 。（1）$$
  第二个边界通过考虑标签和结构信息来改进前一个边界，由[8]，[12]给出为：
$$GED（G_1，G_2）\ge \Gamma （L_{V_1}，L_{V_2}+\Gamma （L_{E_1}，L_{E_2}），（2）$$
其中对于任何X和Y，$\Gamma (X，Y）=max（|X|，|Y|）-|X\cap Y|）$。

定义3：(最大)公共子结构

  给定两个图$G_1$和$G_2$。如果$\exists H_1\subseteq G_1$和$H_2\subseteq G_2$使得$G\cong S（H_1）\cong S（H_2）$，则未标记图$G=（V，E）$被认为是$G_1$和$G_2$的共同子结构。如果不存在其他公共子结构$G^{\prime }=（V^{\prime }，E^{\prime }）$使得$|E^{\prime }|>|E|$（同理顶点也是），则公共子结构$G$是最大公共边（顶点）子结构。 (即$|V^{\prime }|>|V|$）。

  上图是两个比较图$G_1$和$G_2$的例子。边上的数字是它们的id，每个边$e_k$定义为：$e_k=（u_i，u_j）$或$e_k=（v_i，v_j），i<j$。

例1：

  图1显示了两个比较图$G_1$和$G_2$.$GED（G_1，G_2）=2$，因为可以用最少的两个编辑操作将$G_1$转换为$G_2$，
  如下所示：边$（u_1，u_2）$的删除操作和插入标签为$b$的新边$（u_1，u_4）$的边。根据公式2，值$$\Gamma （L_{V_1}，L_{V_2}+\Gamma （L_{E_1}，L_{E_2}）=[4-（|\{C，B，B，B\}\cap \{C，B，B，B\}|）]+[4-（|\{a，a，b，b\}\cap \{a，b，b，b\}|）]=[4-4]+[4-3]=1$$是$GED（G_1，G_2）$全局标签下界.$S（G_1）$是边和顶点的最大公共子结构，因为它具有4个边和4个顶点。

  计算图编辑距离是NP难题[6]。为解决图编辑距离计算的高复杂性，目前仅进行了很少的工作。接下来，我们概述最新的GED计算方法，并强调它们的局限性。下文中，将比较图$G_1$和$G_2$称为源图和目标图。它们的边（顶点）分别称为源边缘和目标边（顶点）。

B. GED计算：A *方法

  基于A * 算法的方法是图编辑距离计算的最新方法，它以最佳优先方式探索源图和目标图之间所有可能的一对一顶点映射9 – [10] [11] [12]。 A * 维护一组局部顶点映射及其诱导的编辑成本。在每个搜索状态下，它都会以最小的诱发编辑代价来扩展部分映射，以进行扩展，其中未映射的目标顶点以及空顶点（带有特殊标签的虚拟顶点）可能是扩展的候选对象。为了将选择过程引导到最有希望的局部映射，然后完善与每个局部映射相关的编辑成本，以包括对其余部分（两个图的未映射边和顶点）的编辑距离的启发式估计。 A * 保证，如果启发式估计值是其余部分的编辑距离的下限，则选取的第一个完整映射是最佳的。如果源顶点和目标顶点都出现在该映射中，则该顶点映射已完成，否则为部分映射。在搜索结束并且有一些未映射目标顶点的情况下，为了完成映射，将在源图中对每个未映射目标顶点执行顶点插入。.

  从数学形式上来表示，给出源图和目标图 $G_1=（V_1，E_1，l_1）$和 $G_2=（V_2，E_2，l_2）$。让源顶点按$（u_1，u_2，\dots ）$顺序处理，$f(V_1）=\{f（u_1），\dots ，f（u_{i-1）}\}$是要扩展的局部映射，并且 $c(f)$表示其相关的编辑成本。成本$c(f)$定义为：$$c(f)=g（f）+h(f)$$，其中$c(f)$代表对映射顶点及其隐含边编辑操作的推断出来的编辑成本，$h(f)$是剩余部分的编辑成本的下限。局部映射$f$遍历搜索空间时，一次扩展一项。对于新扩展的每个可能值$f(u_i)$，即来自值 $（V_2/f(|V_1|)）\cup \{v^n\}$，其中$v^n$是空顶点，$l_2(v^n)\notin \sum$ .构造出的新的局部映射 $$f（V_1）=\{f（u_1），\dots ，f（u_{i-1}），f（u_i）\}$$以及$c(f)$的计算（见下文）。如果size 为$|V_1|$的映射 $f$有一些未映射的目标顶点，为了完成映射，在源图中为每个未映射的目标顶点插入一个顶点，并且$g(f)$ 修改为包括插入的顶点的成本及其隐含的边编辑操作。

  上图解释了A*算法映射新的顶点成本更新

  算法Update_PED（图2）根据最近的扩展 $f(u_i)$更新$g(f)$ 。首先评估最近映射的顶点的编辑成本$f(u_i)$（第1–2行），然后接下来的算法评估其隐含的边（第3–10行）的成本。
  隐式边(由于映射顶点$f(u_i)$可能产生的边，这条边可能在图中，也可能不在)编辑操作的计算公式为：入射到$u_i$的边， 这条边和其他顶点已经匹配就把这条边删除。也就是说，如果 $（f(u_j,f(u_i))，j<i$不是一条目标边，就把这条边删了,并且如果$（f(u_j,f(u_i))，j<i）$有不同的标签，就重新修改标签。
  对于每个匹配的顶点$u_j（u_j不相邻u_i），j<i$ , 如果插入一条边$（f(u_j,f(u_i))，j<i）$是目标边，插入这条边。
  更新中$h(f)$取决于所使用的启发式方法。10通过二分匹配给出了剩余部分之间的编辑距离的估计。12使用剩余部分的全局标签下界作为启发式估计。
补充：7行表示，如果源边（G1俩个点构成所形成的边存在）并且目标边（G1中映射的俩点构成的边）存在，那么看看俩条边的标签是否相同，同则代价是0，否则代价为1.

  基于A*方法的方法面临许多问题。

1. 首先，局部映射的数量变得非常大，尤其是在比较大型图时。这些映射大多数都不能丢弃，必须一直维护到搜索的最后阶段。发生这种情况是因为当前的unpromising的局部映射（即编辑成本较高的映射）有机会在搜索的高级阶段进行扩展。结果，需要巨大的内存。
2. 第二，寻找最小成本的局部映射来扩展是昂贵的。如果使用优先级队列，此操作需要空间复杂度 $O(logn)$，其中$n$是保留的部分映射的数量。
     因此，主要的挑战是当比较图较大且编辑距离较远时的图。比较图越大越远的图，需要维护和处理的局部映射的数量越大。最后，更新相关局部映射 $f$的编辑费用$c(f)$计算上比较昂贵，并且必须在单独的阶段针对每个可能的映射完成扩展。

  显然，此类问题严重阻碍了 A* 算法在实际应用程序中使用。为了解决这些问题，在本文中，我们提出了一种用于图编辑距离计算的新颖方法，称为CSI_GED，该方法可将内存需求降至最低，并缩放到较大和较远的图。接下来，我们介绍新方法的工作原理。

第三节 CSI_GED：使用公共子图同构计算图编辑距离

  在开发有效的GED计算算法时，应考虑两个主要问题。

1. 第一个是找到一种方法来利用在每个搜索状态下计算的部分编辑成本，
2. 第二个是开发一种遍历技术，该技术可以继续搜索而不依赖于部分映射的全部信息。 换句话说，确定最佳编辑路径必须尽可能避免A *方法的问题，以便缩放到大而远的图。

  下面，我们将GED计算问题与比较图中枚举所有常见子结构的问题联系起来。
  给定两个图$G_1=（V_1，E_1，l_1）$和$G_2=（V_2，E_2，l_2）$，我们接下来定义任何顶点映射$f$下的保留边。

定义4: 顶点映射的保留边

  给定一个顶点映射$f：V_1\to V_2\cup v^n$。 如果$（f（u），f（u^{\prime }））\in E_2$，则未标记的源边$（u，u^{\prime }）\in E_1$被称为在$f$下保留。 如果$\exists （u，u^{\prime }）\in E_1$，且$v=f（u）和v^{\prime }=f（u^{\prime }）$，则未标记的目标边$（v，v^{\prime }）\in E_2$被称为$f$下的保留边。

  令$E\subseteq E_1$和$E^{\prime }\subseteq E_2$表示顶点映射$f$下保留的源边和目标边的集合。 考虑与保留边相关的两组顶点，即$V={\bigcup }_{（u，u^{\prime }）\in E}\{u，u^{\prime }\}$和$V^{\prime }={\bigcup }_{（v，v^{\prime }）\in E^{\prime }}\{v，v^{\prime }\}$， 称为保留的源顶点和目标顶点。 显然，两个图$G=（V，E）$和$G^{\prime }=（V^{\prime }，E^{\prime }）$具有相同的结构。 因此，由$f$的未标记保留边$E$及其相关的未标记顶点$V$组成的未标记图$G=（V，E）$是由$f$诱导的$G_1$和$G_2$的常见子结构。 公共子结构G可以断开连接，即确定它不是唯一的。

例2：

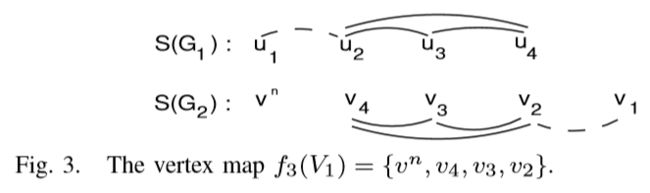
  考虑比较图1中$G_1$和$G_2$。定义三个映射
$$f_1,f_2,f_3：V_1\to V_2\cup V^{null}，$$
$$f_1(V_1)=\{v_1，v_2，v_3，v_4\}，$$
$$f_2（V_1）=\{v_1，v_3，v_4，v_2\}$$
$$f_3（V_1）=\{v^{(null)}，v_4，v_3，v_2\}$$。图3显示了映射$f_3$。图中保留边由粗体曲线显示。虚线曲线表示未保留的。通过其保留的边及其关联的顶点，因此可以给出$f_3$公共子结构，即$G^{{}^{\prime \prime \prime }}=（u_2，u_3，u_4)，（u_2，u_3），（u_2，u_4），（u_3，u_4））$。同时$f_1$和$f_2$的公共子结构也给出为 $G^{\prime }=S（G_1）$ 和 $G^{{}^{\prime \prime }}=G^{{}^{\prime \prime \prime }}$。$G^{\prime }$ 因为它有4个边和4个顶点，所以它边和结点有最大值。

定理1：映射$f$的的编辑成本$g(f)$

  给定两个图 $G_1=（V_1，E_1，l_1）$ 和 $G_2=（V_2，E_2，l_2）$和一个顶点映射$f：V_1\to V_2\cup V^{(null)}$。让$G=（V，E）$ 是 图$G_1$ 和 $G_2$ 的公共子结构，$G$是由$f$ 推断出的。假设$G^{(l_1)}$和$G^{（l_2）}$是公共子结构图$G$的对应的$G_1,G_2$的子图。$G^{(l_1)}$和$G^{（l_2）}$是通过重新覆盖标签得到的。映射$f$的的编辑成本 $g(f)$如下定义：
$$g（f）=c（G^{(l_1)}，G^{（l_2）}）+|V_2\setminus f（V_1）|+\lambda +\sum _{i=1}^2（|E_i|-|E|）（3）$$
$c_f（G^{(l_1)}，G^{（l_2）}）$是公共子结构编辑成本，$|V_2\setminus f（V_1）|$ 是一组未匹配的目标顶点的集合，并且$\lambda =\Gamma (L_{（V_1\setminus V）}，L_{（f（V_1）\setminus V)})$。

证明：
  映射$f$产生一个转变 $G_1$个 进入 $G_2$编辑路径 $P$。 操作$P$ 可以分为三组编辑操作：边删除组$D$，顶点/者边插入组$I$和顶点/边重新标记组 $R$。
  删除组$D$包括删除所有未保留的源边。这些边在目标图中没有对应部分。有$|E_1|-|E|$条这样的边。
  插入组$I$包括在源图中将对应于不匹配目标顶点的顶点插入，即插入$|V_2\setminus f（V_1）|$个顶点。 它还包含将边插入到源图中，对应于未保留的目标边，即插入$|E_2|-|E|$条边缘。
  重新标记操作组$R$包括在$G^{l_1}$和未保留的源顶点$V_1\setminus V$上重新标记。 前者计算为具有不同标签的$G^{l_1}$和$G^{l_2}$的相应顶点和边的数量。 该数字为：$$c_f（G^{l_1}，G^{l_2}）=|（u，u^{\prime }）\in E，l_1（u，u^{\prime }）\ne l_2（f（u），f（u^{\prime }））+|u\in V，l_1（u）\ne l_2（f（u））|$$后者被计算为具有与相应目标标签不同的标签的未保留源顶点的数量，即$$\Gamma (L_{(V_1\setminus V）}，L_{(f（V_1)/V）})$$

  基于定理1，一旦确定了其相应的公共子结构,计算完整的顶点映射$f$的induced的编辑成本变得容易而直接。例3刻画了$G_1$个和 $G_2$的 一个公共的子结构可以产生低于最高成本的编辑成本。

例3：

  比较图1中$G_1$ 和 $G_2$，以及在例2中定义的三个映射 $f_1,f_2和f_3$。使用 $f_3$ 将$G_1$转变为$G_2$转换的编辑成本等于8; 可以根据induced的公共子结构将其计算为：

1. 删除未保留的源边$（u_1，u_2）$，
2. 插入 $v_1$,即插入未匹配的目标顶点，
3. 插入 $（v_1，v_2）$，即插入未保留的目标边，
4. 4 个在公共子结构上重新标记操作。其中在源顶点上两个：$u_2$ 和$u_3$，
   在源边上两个： $（u_2，u_4）$ 和 $（u_3，u_4）$
5. 并在未保留的源顶点 $u_1$ 上执行重新标记操作（相当于 $u_1$删除）。

  同理可得$g（f_1）=5$ 和$g（f_2）=2$。因此，由$f_2$是最佳选择。
  请注意，在例3中，尽管$f_2$ 和 $f_3$ 生成相同的公共子结构，它们在该结构上产生不同的编辑成本。

  这样，可以提出一种计算图编辑距离的新颖方法。此方法表明枚举$G_1$ 和 $G_2$所有常见的子结构同构（简称CSI）,并为每个枚举的对象计算相应的编辑成本，如公式3所示。

  然后，将俩个图编辑距离计算为这些公共子结构所产生的成本的最小值。在图4中概述了名为CSI_GED的方法（CSI：下面的粗体字母：Common Substructure Isomorphism based Graph Edit Distance基于公共子结构同构的图编辑距离），定理2验证了其完整性。

定理2：（完整性）

  给定两个比较图 $G_1$个 和 $G_2$。 $CSI\_GED(G_1,G_2)$ 返回 $G_1$和 $G_2$之间的编辑距离 。

  CSI_GED方法可以减少获得编辑成本的计算开销，即每个顶点映射 $f$的 $g(f)$。不幸的是，任何基于顶点的映射去枚举CSI的方法都需要上面所示的同等计算成本。

  在这些方法中，例如， 15为了构造公共子结构，如果目标顶点不违反先前匹配的顶点上的连接，则目标顶点与源顶点匹配。为了检查以前的连接，该方法所进行的计算与基于A ∗的方法中的隐式边编辑操作相同。

  面对这一挑战，CSI_GED通过映射边而不是顶点来构造CSI，也就是说，考虑了边映射而不是顶点映射。映射边使构建CSI时出现的连接检查问题变得容易，下面我们会讨论这个。乍看之下，尽管边映射空间似乎相对较大，但我们接下来表明用于CSI枚举的空间比整个空间小得多。它可能小于稀疏图上基于顶点的映射空间，在许多实际应用中都是这种情况。

A. 枚举公共子图同构

   为了匹配边，我们将任何目标边视为有序的顶点对。因此，对于任何目标边$e=（v，v\prime ）\in E_2$，让 e^r= （v′，v ） 表示其反向边，${\tilde{E}}_2^r$= { e ，e^r：e∈ E2}表示目标边的扩展集。当且仅当 v 和 v′ 与u和 u′分别匹配，我们说目标边e′= （v ，v ′）∈${\tilde{E}}_2^r$匹配上了源边 e = （u ，u ′）∈ E₁，符号表示为 e → e′。接下来，我们给出了任何映射在识别公共子结构时必须满足的属性。

引理1：

  给定两个比较图$G_1$= （V₁，E₁，l₁） 和 $G_2$= （V₂，E ₂，l ₂）。映射$f$:E₁$\to$E₂∪ { eⁿ}是一个边的映射(eⁿ是空边)，当且仅当e----->f(e)，其中e属于E₁中的任何一条边。如果满足在以下情况，边映射$f$定义了一个公共的子结构，
（1）仅允许将一个或多个源边映射到空边；
（2）对于任何两个相邻的源边e = （u ，u′） 和 e′= （u ，w ） 如果 f（e ）≠ $e^n$ 和 f（e′）≠ eⁿ 那么它们必须在匹配连接顶点时都连接顶点u 。

  引理1表明，考虑用于CSI枚举的边映射的空间比原始空间小得多。在下文中，边映射f 定义为公用子结构,表示成索引边的多重集和：
$$f(E_1)=\{e_{i_1},e_{i_1},...,e_{i_{|E_1|}}\}$$
  其中e_ij表示e_j的匹配边， 它是从有限的可能的集合中选择出来的，集合为 P_j⊆ E₂∪ { eⁿ}，其中eⁿ是唯一可以在 f（E₁）中重复的边。

  为了CSIs的枚举，CSI_GED使用回溯的方去遍历边映射空间。回溯将边的映射当做是树状结构排列。其工作方式如下。:
  最初边的映射f是空的; 随着遍历搜索空间，它一次扩展一个边。映射f的长度与搜索树中相应节点的深度相同。给定长度l的局部边映射 f（E_l）= { e_i1， e_i2… ，e_il-1}，下一个扩展的可能值 e_il来自一个子集 C_l⊆ P_l，称为组合集。如果e′∈ P_l− C_l，那么回溯算法不会考虑根节点是f_l+1= { e_i1， e_i2… ，e_il-1,e^’}的子树中的节点。由于此类子树已从原来的搜索空间中删除，因此C_l也称为修剪。

  图5概述了回溯算法。主循环尝试用当前组合集中 C_l 中的每一个边 e′，去扩展部分边映射f_l 。

图5算法循环过程（1-10）如下：

第一步（第2行）是计算f _l+1。可以简单地通过扩展目标边e′来实现。

第二步（第3行）在第二步结束后，e′ 及其相反的边 ${e^{{}^{\prime }}}^r$标记为已经匹配。

第三步（第5行）是提取新的扩展集P _l，它是由还没有进行匹配的目标边 $e\in \widetilde{E_2}$组成的。

第四步（第6行）是为下一个pass创建一个新的组合集，用来进行有效的扩展。如果目标边满足引理1的第二个条件，即目标顶点的端点与先前匹配的端点一致，则它是有效的扩展。
  因此，组合集 $C_{l+1}$由可能集合 $P_{l+1}$中的那些边组成，这些边在用于扩展 $f_{l+1}$时会产生一个公共子结构。不在组合集中的任何边均指修剪的子树。

第五步（第7行）是为每个扩展递归调用 $CSI-backtrack$算法。

第六步（第8行），完整的映射f 找到，将其添加到 CSI，即完整的CSI的集合。

  如上面所示，回溯方法执行了搜索空间的深度优先遍历，从而提供了有效的存储操作，解决了A*内存访问的主要问题。此外，通过在每个边映射$f$上维护一个顶点映射$M$以将映射存储在已经匹配的边的最终顶点上，可以容易地检查可能扩展的有效性。当扩展映射f时，新的目标边（v ，v ′）如果要映射源边 （u_i，u_j），非空集合M（i）或M（j）必须等于v或v’，才能有效扩展。
  定理3给出了CSI_GED所考虑的边映射空间大小的上限估计。

定理3：CSI_GED的搜索空间

CSI_GED决定了搜索空间大小的大小为
$$O（|E_2|\times (|V_2|/2-2)!\times （d-1{)}^{|E_1|-|V_1|/2})$$其中 d 是目标图的最大顶点度。

证明：
  首先，在不失一般性的前提下，假设$G_1$和$G_2$的顶点数均为偶数，并且$|V_1|\ge |V_2|$。由于$\widetilde{E_2}\cup e^n$是每个边$e_i\in E_1$的匹配候选集，因此边映射搜索空间的总大小为$$\prod _{i=1}^{|E_1|}|{\tilde{E}}_2|$$但是，由CSI_GED考虑的搜索空间的实际大小计算为$$S=\prod _{i=1}^{|E1|}|C（e_i）|$$，其中$C（e_i）\subseteq \widetilde{E_2}$是搜索中的有效候选集。要匹配的第一源边具有等于$|\widetilde{E_2}|=2\times |E_2|$的候选数。
  为了计算每个剩余源边$e_i\in E_1$的有效候选者数量，我们首先在搜索时将这些边缘分类为两种类型：自由边和捆绑边。
  如果一条边与至少一个先前匹配的边相邻，则该边缘被称为捆边，用$e^t$表示，否则，将其称为自由边并用$e^f$表示。令F和T表示自由边和捆绑边的集合。因此，$$S=\prod _{j=1}^{|F|}|C（e_j^f）|\prod _{k=1}^{|T|}|C（e_k^t）|$$。自由边缘的数量最多为$|V_1|/2$，即$|F|\le |V_1|/2$，因为任何一组自由边缘$F$都表示$G_1$中的最大边缘匹配，最大值为$|V_1|/2$——即大小最大边缘匹配。计算每个自由边的有效候选者数量为$\frac{|V_2|}{2}-k$，其中$k$是先前匹配的目标边缘的数量，$\frac{|V_2|}{2}$是$G_2$中最大边缘匹配的大小。因此，$$\prod _{j=1}^{|F|}|C（e_j^f）|=2|E_2|\times \prod _{j=1}^{|V_1|/2-1}（|V_2|/2-1-j）=O（|E_2|\times （|V_2|/2-2)！）$$，因为$|V_1|\ge |V_2|$和$2|E_2|$是第一个匹配的源边缘的候选数。
  考虑到绑边，有两种情况。
  在第一种情况下，绑边仅与一个先前匹配的边相邻。在这种情况下，最多存在$d-1$个有效候选，其中$d=ma{x}_{v_j\in V_2}（deg（v_j））$。
  在第二种情况下，绑边连接到两个先前匹配的边。对于每个这样的边缘，只有一个有效的候选者。因此，$$\prod _{k=1}^{|T|}|C（e_k^t）|\le \prod _{k=1}^{|T|}（d-1）=（d-1{）}^{|T|}。$$由于$|T|$至少为$|E_1|-|V_1|/2$，则空间大小为$$S=O（|E_2|\times （|V_2|/2--2）！\times （d-1{)}^{|E_1|-|V_1|/2）}）$$

  从定理3可以清楚地看出，CSI_GED 所考虑的空间，比尺寸为$O（|V_2{|}^{|V_1|})$ 的基于顶点的映射空间小得多，尤其是在比较图稀疏时。 这是因为在稀疏图³

中，边的数量$|E_1|$ 非常接近顶点数$|V_1|$ ，且$d\ll |V_2|$ 。 而且，$(|V_2|/2-2）！\ll （|V_2|/2-2）|V_1|/2$ 。 仅当目标图是度为$d=|V_2|-1$ 且密度完全的完全图时，顶点空间和边空间的大小几乎相同。 在两个图都非常密集的情况下，即$|E_1|\gg |V_1|且k=|V_2|$ ，则顶点映射空间较小。

例4：

  考虑图1中的比较图$G_1$和$G_2$。图6显示了$G_1$和$G_2$的完整边映射搜索树的一部分，其中第i层上的节点表示可能与源边$e_i\in E_1$匹配的目标边。
   如图所示，源边根据给定的源边顺序每一次映射到一条目标边。 因此，内部节点对应于部分边映射，而其余节点则对应于完整的边映射。 回溯搜索空间可能比整个空间小得多。
  例如，我们从$f_0=\varnothing$和$C_0={\tilde{E}}_2\cup e^n$开始。 在第1层，将$C_0$中的每个项目依次添加到$f_0$中。 例如，将$e_1=（v_1，v_2）$添加以获得$f_1=e_1$。 然后将$e_1$和$e_1^r$标记为匹配。 对于$e_1$的可能集合$P_1$由${\tilde{E}}_2$中所有尚未匹配的目标边组成。但是，由于$e_2=（v_2，v_3）$，$e_4=（v_2，v_4）$和$e^n$是唯一有效的扩展，因此修剪以$e_2^r$，$e_3$，$e_3^r$和$e_4^r$为根的子树。
  比较大型图时，CSI的数量变得很大。 庞大的搜索空间是回溯的主要挑战。 为了迎接这一挑战并开发有效的CSI_GED算法，需要新的启发式方法才能从回溯树中删除整个分支。 下面我们描述用于优化CSI_GED的不同启发式方法。

第四节 优化CSI_GED

  对于最大化公共子结构同构问题，现在目前的方法是基于顶点的回溯算法，通过子结构的大小修剪搜索空间（15, 3, 16）。但是，在我们的设置中，子结构的大小不起作用，因为我们必须枚举所有常见的子结构。 幸运的是，可以按如下方式使用映射的编辑成本来修剪回溯树。

  由于回溯以深度优先的方式枚举CSI，因此某些CSI将在搜索中先于其他CSI可用。由这些枚举引起的编辑成本实际上是图编辑距离的上限，可用于在某些搜索状态下修剪回溯树的分支。确切地说，把那些具有（预期）较高编辑成本的树节点修剪掉。

  为此，我们没有像图4那样，在CSI列举出来之后，在单独下一个阶段中计算每个CSI引起的编辑成本，而是在枚举CSI的过程中就计算每一个CSI的成本，并为每个部分CSI跟新成本值。如果该值大于当前上限值，则对于可以拓展当前部分CSI的那些公共子结构的搜索将会停止，并继续尝试扩展其他部分CSI。

  在决定在枚举CSI的时候，计算其成本之前，我们需要确定每一个CSI映射$f$的成本$g(f)$到底是怎么组成的。定理1给出的成本值$g(f)$是5个独立值的总和。

$g(f)$解释如下：

第一项的 $c(G^{l_1},G^{l_2})$表示了 $G_1,G_2$的公共子图 $G$的产生的俩个子图 $G^{l_1},G^{l_2}$之间的编辑成本；

第二个和第三个值计算未保留的源边和目标边的数量，分别计算为 $|E_1|-|E|,|E_2|-|E|,$

最后两个值是从没有出现在 $G$中的源点和目标定点的的编辑操作考虑的。对于不匹配的目标顶点，需要进行 $|V_2/f(V_1)|$ 个顶点插入，并且该数目构成了第四个值。

最后一个值来自未保留的源顶点上所需的重新标记。

  将前两个成本注入CSI构建十分容易。给定搜索状态，如果找到有效的映射扩展，则扩展在该状态下标识的公共子结构；否则，它保持不变，并且源边被映射到空边$e^n$，这意味着删除该边。因此，一方面，根据第一个成本值，在匹配用于拓展映射$f$的源边和目标边所产生的的编辑成本，将会增大$g(f)$。另一方面，根据第二个成本值，删除源边将增大$g(f)$。第三和第四个成本也可以算进来，但需要额外的计算¹

  因此，这些值有待随后进行计算（即在完成映射之后）。第四个值$||V_1|-|V_2||$ 是可以用作每个CSI的初始成本，因为它是全局的并且独立于任何CSI。

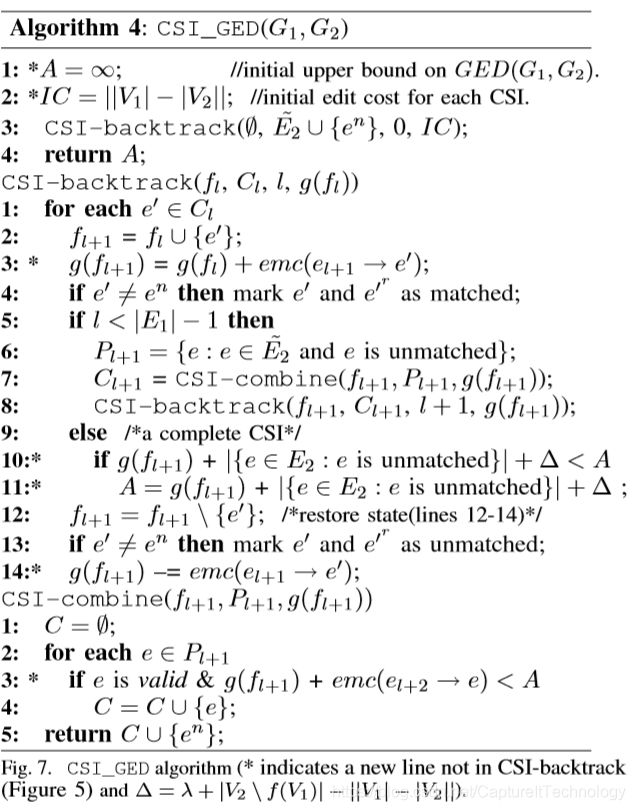
  图7中给出了构建CSI过程中考虑到成本后的CSI_GED新代码。它是$CSI\_backtrack$的直接扩展。主要的补充是将前俩个成本值注入到$g(f)$中，以消除回溯树的分支。除了CSI枚举的主要步骤外，新代码在算法开始的时候添加了一个假设为无穷大的上界$A=\infty$和为每一个$CSI$映射$f$分配的初始化成本$IC=||V_1|-|V_2||$。
  本算法在映射拓展之后添加一个步骤（$CSI\_backtrack$第三行），用来更新$g(f)$，同时也增加了一个步骤$CSI\_backtrack$第10、11行）去更新$A$。为了包含基于上界值的修剪，在$CSI\_combine的$第三行修剪的地方添加新的条件。用来更新$g(f)$的边匹配成本$emc(e\to e^{{}^{\prime }})$定义如下。

定义5：边匹配成本

  给定源边和目标边 e = （u ，u ′） 和 e′= （v ，v′）。将边$e^{{}^{\prime }}$分配给e的成本，称为边匹配成本并表示为 emc(e → e′），给出定义为：$$emc(e\to e\prime ）=\{\begin{array}{rcl}c(u\to v)+c(v^{{}^{\prime }}\to v^{{}^{\prime }})+c(e\to e^{{}^{\prime }})& & e\ne e^n\\ 1& & e=e^n\end{array}$$
  若匹配的项含有相同的标签则c=0，否则c=1⁴

  显然，定义5中的两种情况会更新$g(f)$⁵的前俩项的值。

  为了提高基于上限的修剪，首先想到的是，不仅仅基于 $g(f)$这 一项进行修剪，还可以考虑到未映射的边和顶点的编辑距离的下限。但是，在不断扩展的搜索树的每个树节点上计算下限是不切实际的。

在这里，采用了新的高效启发式方法来增强修剪效果。

第一种启发式方法排列目标边，以便能够快速找到更严格的上限

第二种则最大化分配给每个CSI的初始编辑成本。

第三种实现了搜索的预测功能。

  这样的启发式搜索将允许在搜索前期遇到其编辑成本超过上限值的树节点。因此减少了许多分支树的考虑。接下来，我们详细介绍这些启发式方法。

A.给目标边排序

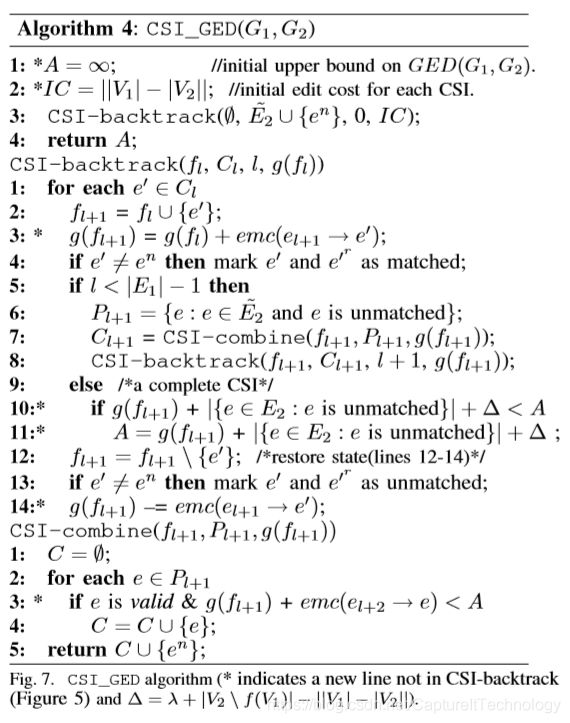
  假定每个有效扩展大小为$l$，部分$CSI$来自相同的目标边的集合${\tilde{E}}_2$（图7中的第6行）。 因此，在树的第$i$层($1\le i\le |E_1|$)处使用的目标边${\tilde{E}}_2$可以这样排序：首先枚举产生更严格上限的那些$CSI$。 采用的排序法将${\tilde{E}}_2$按成本值$C（e_l，e^{\prime }）$的升序排列在树的第i层上，其中函数$C$计算近似图编辑成本，前提是将目标边$e^{\prime }$分配给源边缘$e$。
  为了定义成本函数$C$，我们首先定义边星（围绕边的局部结构）和星匹配成本。

定义6：星图 (这边不想看了，好恶心啊！)

  给定图 G = （V，E ，l ） 和边 e ∈ E。边星e，表示图G是一个子图，它是指和e相连的边构成的子图，用s(e)表示。

定义7：星边匹配费用

  给定两个边 e = （u ，u ′） 和 e′= （v ，v ′），它们分别是俩个图中的源边和目标边。星边的匹配成本，可以用下面的公式表示：
$$smc(e,e^{{}^{\prime }})=emc(e⟶e^{{}^{\prime }})+\Gamma (L_{E_u},L_{E_v})+\Gamma (L_{E_{u^{{}^{\prime }}}},L_{E_{v^{{}^{\prime }}}})$$

其中LE_x是和顶点x相连的边的多重集合，不包括核心边的标签。

定义8：余星图

  给定图 G = （V，E，l ） 和边星 s(e)，e∈ E。定义余星图G^e是在原图中切除边星之后的子图。
 给定源边和目标边 e_l 和 e^’.假设$G_1^{e_l}=(V_1^{{}^{\prime }},E_1^{{}^{\prime }},l_1^{{}^{\prime }})$和$G_2^{e_{’}}=(V_2^{{}^{\prime }},E_2^{{}^{\prime }},l_2^{{}^{\prime }})$分别是 $s(e_l)和s(e^{{}^{\prime }})$在其原图中的余图。由此，通过星图和余图的定义，得到了俩条边映射的成本：
$$C(e_l,e^{{}^{\prime }})=smc(e_l,e^{{}^{\prime }})+\Gamma (L_{V_1^{{}^{\prime }}},L_{V_2^{{}^{\prime }}})+\Gamma (L_{E_1^{{}^{\prime }}},E_{V_2^{{}^{\prime }}})$$

例5：

 下面举例通过星图和余图的定义，计算边的映射成本的例子。在图1和图2中分别给出源边$e=（u_3,u_2）,目标边e^{{}^{\prime }}（v_3,v_4)$的星图，那么可以得出余图分别为$G^e=((u_1,u_4),\varnothing ，l_1),G^{e^{{}^{\prime }}}=((v_1,v_2),(v_1,v_2)，l_2)$。通过如下计算可以得出俩条边的映射成本为5：
 
由$$C(e_l,e^{{}^{\prime }})=smc(e_l,e^{{}^{\prime }})+\Gamma (L_{V_1^{{}^{\prime }}},L_{V_2^{{}^{\prime }}})+\Gamma (L_{E_1^{{}^{\prime }}},E_{V_2^{{}^{\prime }}})$$可知，
$$C(e_l,e^{{}^{\prime }})=smc(e_l,e^{{}^{\prime }})+\Gamma (L_{V_1^{{}^{\prime }}},L_{V_2^{{}^{\prime }}})+\Gamma (L_{E_1^{{}^{\prime }}},E_{V_2^{{}^{\prime }}})=2+1+1=4$$

  其中余图的顶点和边的标签的界分别计算为0和1。如果源边按照$$E=((u_1,v_2),(u_2,v_3),(u_3,v_4),(u_4,v_5))$$的顺序处理，那么在树的第二层，目标边应该按照$$((v_3，v_4），（v_3，v_2），（v_2，v_3），（v_2，v_1），（v_4，v_3），（v_2，v_4），（v_4，v_2），（v_1，v_2）)$$进行排列 ，其中成本值C是按边星图$s(u_2，u_3)$计算的，分别为：$$(2,2,3,4,5,5,6,6)$$。

B.最大化初始公共子图同构（CSI）成本

  可以最大化分配给每个公共子图同构CSI的初始成本值，从而包括图大小差异和图顺序差异。也就是说，分配给每个公共子图同构CSI的初始成本$f$可以定义为成初始化成本$IC=||V_1|-|V_2||+||E_1|-|E_2||$。将图大小差添加到初始成本需要修改边匹配成本$emc$，尤其是已删除的源边上。也就是说，在匹配边的过程中，我们不考虑评估源边的删除作为编辑成本（定义5），而是考虑到$|E_1|和|E_2|$可能出现的不同值情况来进行修改。以下定理涵盖了这些情况。

定理4：扩展$f$删除源边成本

 给定一个空的公共子图同构映射$f$，且初始成本 $g(f)=||V_1|-|V_2||+||E_1|-|E_2||$，在扩展$f$的时候删除源边的成本如下计算：
$$emc(e⟶e^n)=\{\begin{array}{rlrlrl}2,& & & & & |E_1|\le |E_2|;;\\ 2,& & & & & |E_1|>|E_2|\&k\ge (|E_1|-|E_2|);\\ 0,& & & & & |E_1|>|E_2|\&k<(|E_1|-|E_2|);\end{array}$$
其中 ķ 是先前删除的源边的数量。

证明：
关于源边和目标边的数量，我们有两种可能的情况，即$|E_1|和|E_2|$。
 情形一：$|E_1|\le |E_2|$,转变G₁变成同构的图 G₂，我们最初需要在G₁中添加$|E_2|-|E_1|$条边使两个图的边数量均等。因此，在公共子图同构CSI构造期间，对于每个删除的源边，都需要在源图中的某处添加一个新边，从而进行两次编辑操作，以保持相等数量的源边和目标边。
 情形二：$|E_1|>|E_2|$。初始化中$g(f)=|E_1|-|E_2|$意味着删除多达此数量的源边不会影响编辑成本，因为初始化中已经添加了相等的成本。用尽初始成本后，即删除$|E_1|-|E_2|$ 源边后，任何后续的源边删除都需要在源图上添加另一条边，从而进行两次编辑操作，以保持相等数量的源边和目标边。

 除了最大化分配给每个CSI的初始成本外，定理4还可以平滑注入未保留目标边的编辑费用$|E_1|-|E|$，纳入公共子图同构CSI枚举过程。相应地修改了图7中的CSI_GED伪代码，以适应边匹配成本和初始成本值的新定义。未保留目标边的数量也从CSI回溯的第10和11行的后续计算阶段中删除。

C.基于预测（look-ahead）的修剪

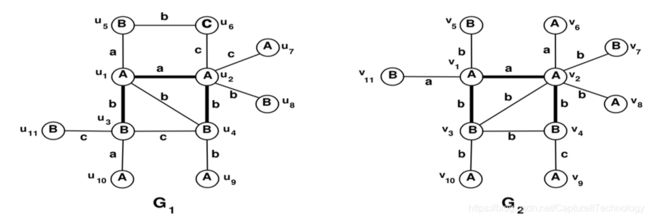
  以图9源图和目标图 $G_1和G_2$为例。这两个图的顶点数相同，但是$G_1$个有一条额外的边。因此，分配给每个公共子结构枚举$CSIf$的初始成本等于1。下面考虑将粗体目标边与粗体源边匹配的部分公共子结构枚举CSI的映射 $f$。由于公共子结构在子图上引起的编辑成本等于零，此部分公共子结构枚举CSI的编辑费$g（f）$等于1。对于任何大于1的上界，基于此成本值$g（f）$，目前无法停止扩展此部分$CSI$。

 在本小节中，我们介绍另一个成本函数$g^{{}^{\prime }}（f）$ 有效修剪此类情形，除$g（f）$之外，每个公共子结构的枚举映射$f$都要维护该函数。 此函数实现了前瞻性。也就是说，它能够在搜索中提前在搜索树的第$i$层中计算编辑成本，并查看其是否大于当前计算的的上界，从修剪映射。

 给定图 G。为其中的一个子图$H⊑G$定义内部邻域和外部邻域。

定义9：子图的内部和外部邻居

  给定图 G = （V，E ，l ） 和一个子图 $H=（V_H，E_H，l）\subseteq G$ 。
子图H的内部邻居定义为：$N_I=\{(u,v)\in E:u,v\in V_H\}$,外部邻居定义为：$N_O=\{(u,v)\in E:u\in V_H\cap v\notin V_H\}$。
  基于一个子图 $H\subseteq G$的内部和外部邻域，定义$H$中顶点的内部度和外部度。用下面的符号表示：顶点的内部邻居为$${d}_I(v)=|\{(u,v)\in N_I(V_H)\}$$顶点的外部邻居为$$d_O(v)=|deg(v)-d_I(v)|$$。

  现在，给定源图和目标图 $G_1和G_2$以及一个部分公共子图枚举映射$f$。假设$M$是通过边映射$f$而产生的顶点映射，新的代价函数$g^{{}^{\prime }}(f)$根据子图的内部和外部邻居产生如下定义。$G_1和G_2$通过映射$f$产生公共子结构$G=(V,E)$,则在图$G_1$中表示的子结构为$g^{l_1}\in G_1$，同理在$G_2$中公共子结构表示为$g^{l_2}\in G_2.$ 代价函数$g^{{}^{\prime }}$中包含四项内容的和：对应顶点度的代价$c_d$,对应的内部邻居边的代价$c_e$，余下边的代价$c_r$，还有通过公共子图枚举CSI的映射$f$，进行图$G_1和图G_2$重新加标签的代价$k$，即$$g^{{}^{\prime }}(f)=c_d+c_e+c_r+k$$

 其中的具体运算如下所示：
度成本$c_d$可以表示为： $$c_d=\sum _{u\in V_{G^{l_1}}}|d_o(u)-d_o(M(u))|+\frac{1}{2}|d_I(u)-d_I(M(u))|,(4)$$
  其中分数$\frac{1}{2}$表示每一个内部的边在运算时都被用过俩次，每一个结束的端点被用过一次
内部边的成本$c_e$可以表示为：
$$c_e=\sum _{u,u^{{}^{\prime }}\in V_{G^{l_1}}}c((u,u^{{}^{\prime }})\to (M(u),M(u,u^{{}^{\prime }}))$$
  其中$(u,u^{{}^{\prime }})\in N_I(V_{G^{l_1}})$，$(M(u),M(u,u^{{}^{\prime }}))\in N_I(V_{G^{l_2}})$，若映射的边标签相同，比如原图中是a，映射的目标边是c，则标签 不同返回1，否则为0。
余边成本$c_r=|n_1-n_2|$表示如下
  其中$n_i=|\frac{E_i}{(N_I(V_{G^{l_i}}))\cup N_O(V_{G^{l_i}})}|,i=1,2$
顶点重新加标签成本$k$如下计算：
$$k=max(\Gamma (L_{V_1},L_{V_2}),h+||V_1|-|V_2|)),$$
其中h是在匹配顶点上重新加标签的数量。

定理5：

  给定两个比较图 $G_1$ 和 $G_2$，以及公共子图同构$CSI$的完全映射$f$。对于任何公共子图同构$CSI$的完全映射$f$ ，有$g^{{}^{\prime }}(f)\le g(f)$。

例6：

  上图 $G_1和G_2$中，假定存在映射$f$,它是公共子结构的一种情形，通过它可以构造一个公共子结构G，和一个顶点映射$M=\{v_1,v_2,v_3,v_4$