基于统计的语言模型-n元语法模型
n-gram模型概述
1、n-gram模型,也称为N元语法模型,是一种基于统计语言模型的算法,n表示n个词语,n元语法模型通过n个词语的概率判断句子的结构。
2、n元语法模型的算法思想:将文本里面的内容按照字节进行大小为N的滑动窗口操作,形成了长度时N的字节片段序列,每个字节片段称为gram。对所有gram的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键gram列表,也就是这个文本的向量特征空间,列表中的每一种gram就是一个特征向量维度。

3、该模型基于马尔科夫假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是Bi-Gram(二元语法模型)和Tri-Gram(三元语法模型)。
4、n-gram模型常见的应用场景:输入法的提示、搜索引擎等
n-gram原理
1、马尔科夫假设
给定时间线上有一串事件顺序发生,假设每个事件的发生概率只取决于前1个或t (t >1)个事件,那么这串事件构成的因果链被称作马尔可夫链。在语言模型中,第i个事件指的是w,作为第i个单词出现。也就是说,每个单词出现的概率只取决于前1个或t个单词:
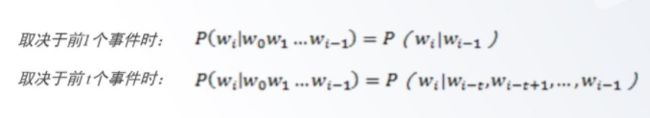
举例,当n=2时,为二元语法模型(Bi-Gram),即每个单词出现的概率只与前1个单词有关,根据公式计算整个句子出现的概率P(S) 为句子中每个单词出现概率的乘积:
P ( S ) = P ( w 1 , w 2 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 ) … P ( w n ∣ w n − 1 ) P(S) = P(w_1,w_2, \dots,w_n) = P(w_1)P(w_2|w_1)P(w_3|w_2)\dots P(w_n|w_{n-1}) P(S)=P(w1,w2,…,wn)=P(w1)P(w2∣w1)P(w3∣w2)…P(wn∣wn−1)
对于句子“今天天气晴朗”,利用Bi-gram时,该句子的概率如下:
P ( 今 天 天 气 晴 朗 ) = P ( 今 ) P ( 天 ∣ 今 ) P ( 天 ∣ 天 ) P ( 气 ∣ 天 ) P ( 晴 ∣ 天 ) P ( 朗 ∣ 晴 ) P(今天天气晴朗) = P(今)P(天|今)P(天|天)P(气|天)P(晴|天)P(朗|晴) P(今天天气晴朗)=P(今)P(天∣今)P(天∣天)P(气∣天)P(晴∣天)P(朗∣晴)
若n=3时,为三元语法模型(Tri-gram),即每个单词出现的概率只与前两个(n-1)单词有关,根据公式计算整个句子出现的概率P(S) 为句子中每个单词出现概率的乘积:
P ( S ) = P ( w 1 , w 2 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 w 1 ) … P ( w n ∣ w n − 2 w n − 1 ) P(S) = P(w_1,w_2, \dots,w_n) = P(w_1)P(w_2|w_1)P(w_3|w_2w_1)\dots P(w_n|w_{n-2}w_{n-1}) P(S)=P(w1,w2,…,wn)=P(w1)P(w2∣w1)P(w3∣w2w1)…P(wn∣wn−2wn−1)
则对于句子“今天天气晴朗”,利用Tri-gram时,该句子的概率如下:
P ( 今 天 天 气 晴 朗 ) = P ( 今 ) P ( 天 ∣ 今 ) P ( 天 ∣ 天 今 ) P ( 气 ∣ 天 天 ) P ( 晴 ∣ 气 天 ) P ( 朗 ∣ 晴 气 ) P(今天天气晴朗) = P(今)P(天|今)P(天|天今)P(气|天天)P(晴|气天)P(朗|晴气) P(今天天气晴朗)=P(今)P(天∣今)P(天∣天今)P(气∣天天)P(晴∣气天)P(朗∣晴气)
2、利用n-gram计算句子出现的概率
当n>1时,为了使句首词的条件概率有意义,需要给原序列加上一个或多个起始符 ,即 w 0 = < B O S > w_0=
同理,为了使句尾的条件概率有意义,也需要加上一个或多个结束符。


对于Bi-gram模型而言, P ( w i ∣ w i − 1 ) P(w_i|w_{i-1}) P(wi∣wi−1)可以使用极大似然估计得到,即:
P ( w i ∣ w i − 1 ) = c ( w i − 1 , w i ) ∑ w i c ( w i − 1 , w i ) = c ( w i − 1 , w i ) c ( w i − 1 ) P(w_i|w_{i-1}) = \frac{c(w_{i-1},w_i)}{\sum_{w_i}c(w_{i-1},w_i)} = \frac{c(w_{i-1},w_i)}{c(w_{i-1})} P(wi∣wi−1)=∑wic(wi−1,wi)c(wi−1,wi)=c(wi−1)c(wi−1,wi)
其中,c()表示子序列在数据集中出现的次数。
对于n-gram模型而言,条件概率的计算方法为:
P ( w i ∣ w 1 , … , w i − 1 ) = c ( w 1 , w 2 , … , w i ) ∑ w c ( w 1 , w 2 , … , w i , w ) = c ( w 1 , w 2 , … , w i ) c ( w 1 , w 2 , … , w i − 1 ) P(w_i|w_1,\dots,w_{i-1}) = \frac{c(w_1,w_2,\dots,w_i)}{\sum_wc(w_1,w_2,\dots,w_i,w)} \\ = \frac{c(w_1,w_2,\dots,w_i)}{c(w_1,w_2,\dots,w_{i-1})} P(wi∣w1,…,wi−1)=∑wc(w1,w2,…,wi,w)c(w1,w2,…,wi)=c(w1,w2,…,wi−1)c(w1,w2,…,wi)
公式有些难以理解,举个例子。
假设一个语料库有三个句子‘今天天气晴朗’,‘今天是个好日子’,‘天气阴’
统计词频如下:
| 今 | 天 | 气 | 晴 | 朗 | 是 | 个 | 好 | 日 | 子 | 阴 | 总共 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 16 |
那使用Bi-gram计算‘今天天气晴’的概率为:
P ( 今 天 天 气 晴 朗 ) = P ( 今 ∣ < B O S > ) ⋅ P ( 天 ∣ 今 ) ⋅ P ( 天 ∣ 天 ) ⋅ P ( 气 ∣ 天 ) ⋅ P ( 晴 ∣ 气 ) ⋅ P ( 朗 ∣ 晴 ) ⋅ P ( < E O S > ∣ 朗 ) = c ( < B O S > , 今 ) c ( < B O S > ) ⋅ c ( 今 , 天 ) c ( 今 ) ⋅ c ( 天 , 天 ) c ( 天 ) ⋅ c ( 天 , 气 ) c ( 天 ) ⋅ c ( 气 , 晴 ) c ( 气 ) ⋅ c ( 晴 , 朗 ) c ( 晴 ) ⋅ c ( 朗 , < E O S > ) c ( 朗 ) = 2 3 × 2 2 × 1 4 × 2 4 × 1 2 × 1 1 × 1 1 = 1 24 \begin{aligned} P(今天天气晴朗) &= P(今|
P ( 今 天 是 个 好 日 子 ) = P ( 今 ∣ < B O S > ) ⋅ P ( 天 ∣ 今 ) ⋅ P ( 是 ∣ 天 ) ⋅ P ( 个 ∣ 是 ) ⋅ P ( 好 ∣ 个 ) ⋅ P ( 日 ∣ 好 ) ⋅ P ( 子 ∣ 日 ) ⋅ P ( < E O S > ∣ 子 ) = c ( < B O S > , 今 ) c ( < B O S > ) ⋅ c ( 今 , 天 ) c ( 今 ) ⋅ c ( 天 , 是 ) c ( 天 ) ⋅ c ( 是 , 个 ) c ( 是 ) ⋅ c ( 个 , 好 ) c ( 个 ) ⋅ c ( 好 , 日 ) c ( 好 ) ⋅ c ( 日 , 子 ) c ( 日 ) ⋅ c ( 子 , < E O S > ) c ( 子 ) = 2 3 × 2 2 × 1 4 × 1 1 × 1 1 × 1 1 × 1 1 × 1 1 = 1 6 \begin{aligned} P(今天是个好日子) &= P(今|
P ( 天 气 阴 ) = P ( 天 ∣ < B O S > ) ⋅ P ( 气 ∣ 天 ) ⋅ P ( 阴 ∣ 气 ) ⋅ P ( < E O S > ∣ 阴 ) = c ( < B O S > , 天 ) c ( < B O S > ) ⋅ c ( 天 , 气 ) c ( 天 ) ⋅ c ( 气 , 阴 ) c ( 气 ) ⋅ c ( 阴 , < E O S > ) c ( 阴 ) = 4 3 × 2 4 × 1 2 × 1 1 = 1 3 \begin{aligned} P(天气阴) &= P(天|