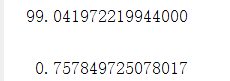数值分析实验四 最小二乘法曲线拟合
一、实验目的
1.使用不同的模型对数据进行最小二乘拟合；
2.分析使用不同模型最小二乘法对数据进行拟合的RMSE(均方根误差)；
3.根据分析结果求出最合理的拟合模型。
二、实验题目
1.用表1-1中的世界人口统计数值估计1980年的人口，求最佳最小二乘法数值估计：
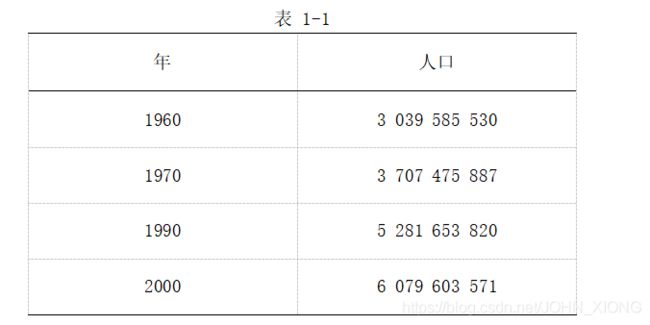(a) 直线；(b) 抛物线。它们都通过这些数据点，并求这些拟合的RMSE。在每一种情形下，估计1980年的人口。哪一种拟合给出最佳估计。（40分）
2. 世界石油产量以每天百万桶计，如表1-2所示，求最佳最小二乘法数值估计：
(a) 直线；(b) 抛物线；© 立方曲线。它们都通过10个数据点。并求这些拟合的RMSE。利用上面的每一种拟合来估计2010年的生产水平。就RMSE而言，那一种拟合最好的代表了这些数据。（60分）
说明：RMSE(root-mean-square error，均方根误差)。
三、实验原理
1、最小二乘法
已知：一组数据（xi，yi）(i = 0,1,…,m)，在函数集合
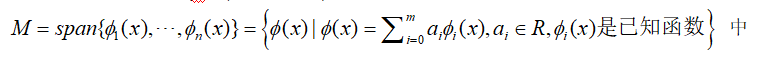
四、实验内容与结果
1.用表1-1中的世界人口统计数值估计1980年的人口，求最佳最小二乘法数值估计：
(a) 直线拟合估计1980年的人口结果及RMSE分析（15分）
1. 程序源码
拟合函数代码
function [population,RMSE] = fit(x,y,n,year)
%FIT 此处显示有关此函数的摘要
% 此处显示详细说明
count_x = length(x);
G = zeros(n+1,n+1);
Gf = zeros(n+1,1);
%计算法方程组等式最左边
for i=1:n+1
for j=1:n+1
m = 0;
for k=1:count_x
m = m + x(k)^(i+j-2);
end
G(i,j) = m;
end
end
%计算法方程组等式右边
for i=1:n+1
m = 0;
for k = 1:count_x
m = m + x(k)^(i-1)*y(k);
end
Gf(i) = m;
end
%列主消元法求系数
[augmentedMatrix,a] = ColMain(G,Gf);
%对系数矩阵进行翻转
a = fliplr(a');
x_new = x(1):5:x(count_x);
pre = polyval(a,x_new);
population = polyval(a,year);
plot(x,y,'r*',x_new,pre,'kx-',year,population,'bo');
legend('原始数据','拟合曲线','1980预测','Location','NorthWest');
%计算RMSE
Gx = polyval(a,x);
sum = 0;
for i=1:count_x
sum = sum + (Gx(i)-y(i))^2;
end
RMSE = sqrt((sum)/count_x);
end
高斯消元求系数代码
function [augmentedMatrix,ans] = ColMain(A,b)
%COLMAIN 此处显示有关此函数的摘要
% 此处显示详细说明
%常量定义
ZERO = 10^(-15);
%增广矩阵
augmentedMatrix = [A b];
[row_a,col_a] = size(A);
[row_b,col_b] = size(b);
%解
ans = zeros(col_a,1);
%先判断A是不是方阵
if row_a ~=col_a
sprintf('矩阵A不是方阵')
return;
end
%判断b是否符合要求
if row_b ~= row_a
sprintf('b的格式为列向量且b的行数和A的行数要相同')
return;
end
%判断b的行和A的行是否一致
if row_a ~= row_b
sprintf('向量b长度必须和矩阵A的行数相等')
return;
end
%进行消元
for col = 1:col_a-1
%找每一列的最大值
maxCol = max(abs(augmentedMatrix(col:row_a,col)));
%判断A是否为系数矩阵
if maxCol < ZERO
sprintf('系数矩阵A是奇异矩阵!程序退出!')
return;
end
%进行交换
for row = col:col_a
if maxCol == ((augmentedMatrix(row,col)))
temp = augmentedMatrix(row,:);
augmentedMatrix(row,:) = augmentedMatrix(col,:);
augmentedMatrix(col,:) = temp;
break;
end
end
%执行消元操作
for row = col+1:col_a
%计算mij
mRowCol = (augmentedMatrix(row,col)/augmentedMatrix(col,col));
%消元
augmentedMatrix(row,:) = augmentedMatrix(row,:)-mRowCol*augmentedMatrix(col,:);
end
end
%将每个解的系数变为1，就相当于是最后除去系数了
for row = 1:row_a
augmentedMatrix(row,:) = augmentedMatrix(row,:)/augmentedMatrix(row,row);
end
%消元后的b
b = augmentedMatrix(:,col_a+1);
%回带求解
ans(col_a) = b(col_a);
for row = col_a - 1:-1:1
ans(row) = 0;
for col = row+1:col_a
ans(row) = ans(row) + augmentedMatrix(row,col)*ans(col);
end
ans(row) = b(row) - ans(row);
end
end
2.计算结果与分析
将数据代入程序中，得到预测的1980年的人口数量大约为：4.527079702000000e+09
RMSE=3.675108816241655e+07
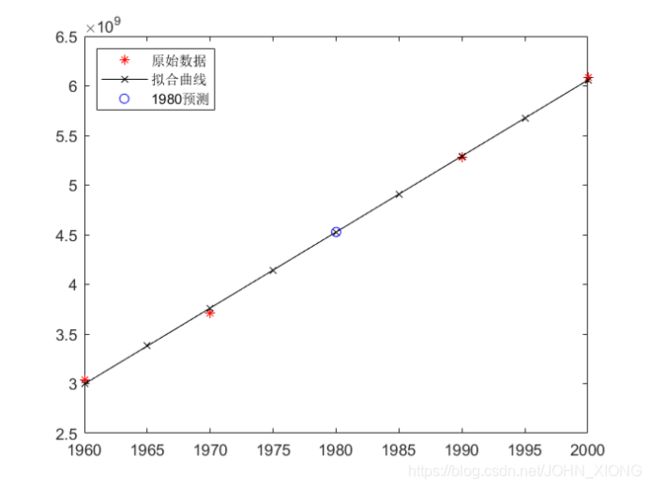
(b) 抛物线拟合估计1980年的人口的结果及RMSE分析（15分）
1. 程序源码
拟合函数代码
function [population,RMSE] = fit(x,y,n,year)
%FIT 此处显示有关此函数的摘要
% 此处显示详细说明
count_x = length(x);
G = zeros(n+1,n+1);
Gf = zeros(n+1,1);
%计算法方程组等式最左边
for i=1:n+1
for j=1:n+1
m = 0;
for k=1:count_x
m = m + x(k)^(i+j-2);
end
G(i,j) = m;
end
end
%计算法方程组等式右边
for i=1:n+1
m = 0;
for k = 1:count_x
m = m + x(k)^(i-1)*y(k);
end
Gf(i) = m;
end
%列主消元法求系数
[augmentedMatrix,a] = ColMain(G,Gf);
%对系数矩阵进行翻转
a = fliplr(a');
x_new = x(1):5:x(count_x);
pre = polyval(a,x_new);
population = polyval(a,year);
plot(x,y,'r*',x_new,pre,'kx-',year,population,'bo');
legend('原始数据','拟合曲线','1980预测','Location','NorthWest');
%计算RMSE
Gx = polyval(a,x);
sum = 0;
for i=1:count_x
sum = sum + (Gx(i)-y(i))^2;
end
RMSE = sqrt((sum)/count_x);
end
高斯消元求系数代码
function [augmentedMatrix,ans] = ColMain(A,b)
%COLMAIN 此处显示有关此函数的摘要
% 此处显示详细说明
%常量定义
ZERO = 10^(-15);
%增广矩阵
augmentedMatrix = [A b];
[row_a,col_a] = size(A);
[row_b,col_b] = size(b);
%解
ans = zeros(col_a,1);
%先判断A是不是方阵
if row_a ~=col_a
sprintf('矩阵A不是方阵')
return;
end
%判断b是否符合要求
if row_b ~= row_a
sprintf('b的格式为列向量且b的行数和A的行数要相同')
return;
end
%判断b的行和A的行是否一致
if row_a ~= row_b
sprintf('向量b长度必须和矩阵A的行数相等')
return;
end
%进行消元
for col = 1:col_a-1
%找每一列的最大值
maxCol = max(abs(augmentedMatrix(col:row_a,col)));
%判断A是否为系数矩阵
if maxCol < ZERO
sprintf('系数矩阵A是奇异矩阵!程序退出!')
return;
end
%进行交换
for row = col:col_a
if maxCol == ((augmentedMatrix(row,col)))
temp = augmentedMatrix(row,:);
augmentedMatrix(row,:) = augmentedMatrix(col,:);
augmentedMatrix(col,:) = temp;
break;
end
end
%执行消元操作
for row = col+1:col_a
%计算mij
mRowCol = (augmentedMatrix(row,col)/augmentedMatrix(col,col));
%消元
augmentedMatrix(row,:) = augmentedMatrix(row,:)-mRowCol*augmentedMatrix(col,:);
end
end
%将每个解的系数变为1，就相当于是最后除去系数了
for row = 1:row_a
augmentedMatrix(row,:) = augmentedMatrix(row,:)/augmentedMatrix(row,row);
end
%消元后的b
b = augmentedMatrix(:,col_a+1);
%回带求解
ans(col_a) = b(col_a);
for row = col_a - 1:-1:1
ans(row) = 0;
for col = row+1:col_a
ans(row) = ans(row) + augmentedMatrix(row,col)*ans(col);
end
ans(row) = b(row) - ans(row);
end
end
3.计算结果与分析
将数据代入程序中，得到预测的1980年的人口数量大约为：4.472888283964722e+09
RMSE=1.712971418739812e+07
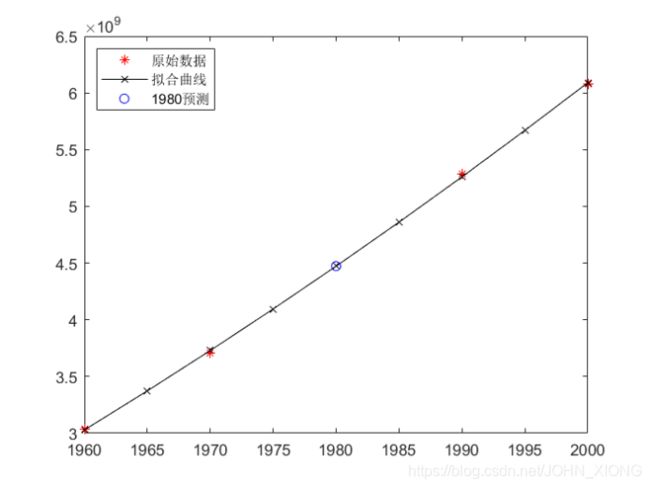
（c）估计1980年的人口，根据拟合的RMSE，比较分析哪一种拟合给出的是最佳估计。（10分）
直线拟合的RMSE=3.675108816241655e+07
抛物线拟合的RMSE=1.712971418743657e+07
我们可以看出，抛物线拟合的RMSE更小，所以抛物线拟合要好一些
世界石油产量，求最佳最小二乘法数值估计：
(a) 直线估计世界石油产量2010年的生产水平，其估计结果及RMSE分析；（15分）
1.程序源码
源程序和上一题的都一样，此处省略
2.计算结果与分析
将数据代入程序中，得到2010年石油产量大约为：83.382272727811142
RMSE = 0.976318096449374
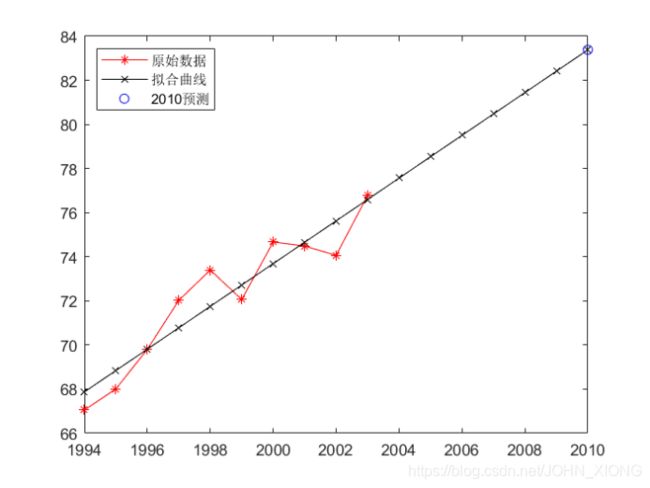
(b) 抛物线估计世界石油产量2010年的生产水平，其估计结果及RMSE分析；（15分）
- 程序源码
源程序和上一题的都一样，此处省略 - 计算结果与分析
将数据代入程序中，得到2010年石油产量大约为：74.411566176742781
RMSE = 0.822676653645600
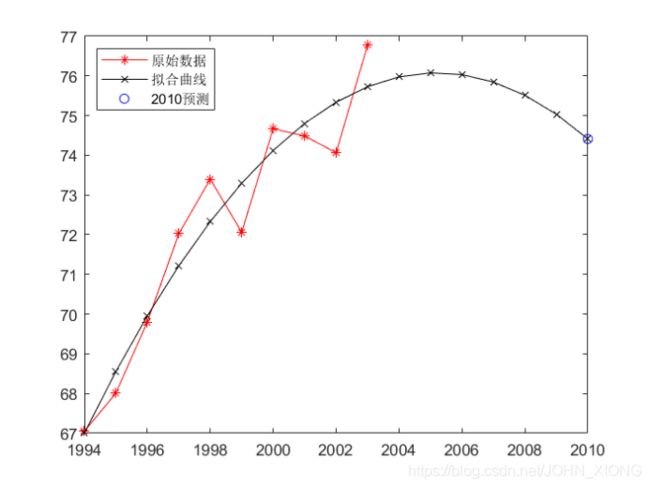
（c）立方曲线估计世界石油产量2010年的生产水平，其估计结果及RMSE分析；（15分）
3. 程序源码
x0 = [1994,1995,1996,1997,1998,1999,2000,2001,2002,2003];
y0 = [67.052000000000000,68.008000000000000,69.803000000000000,72.024000000000000,73.400000000000000,72.063000000000000,74.669000000000000,74.487000000000000,74.065000000000000,76.777000000000000];
u = [2010];
a3 = polyfit(x0,y0, 3);
x_new = [x0 x0(length(x0))+1:1:2010];
pre = polyval(a3,x_new);
petrol_pre = polyval(a3,2010);
plot(x0, y0, 'red*-', x_new, pre, 'kx-',2010,petrol_pre,'bo');
legend('原始数据','三次曲线拟合','2010预测','Location','NorthWest');
xlabel('年份');
ylabel('人口数量');
- 计算结果与分析
将数据代入程序中，得到2010年石油产量大约为：99.041972219944000
RMSE = 0.757849725078017
（d）估计世界石油产量2010年的生产水平，根据拟合的RMSE，比较分析哪一种拟合给出的是最佳估计。（15分）
从上面的结果中，我们可以看出：
直线模型的RMSE=0.976318096449374
抛物线模型的RMSE=0.822676653645600
立方曲线模型的RMSE=0.757849725078017
所以立方曲线模型拟合效果更好