数值分析:数据的最小二乘拟合
1 实验目的
在已知某天在不同时间的前温度高低,借用最小二乘法确定这一天的气温变化规律。通过MATLAB编程,选取适当函数进行求解绘图。
2 实验内容
假定某天的气温变化记录如下表所示:
| 时间(t) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 温度(x(t)) |
15 |
14 |
14 |
14 |
14 |
15 |
16 |
18 |
20 |
22 |
23 |
25 |
28 |
| 时间(t) |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
| 温度(x(t)) |
31 |
32 |
31 |
29 |
27 |
25 |
24 |
22 |
20 |
18 |
17 |
16 |
试用最小二乘法确定这一天的气温变化规律,考虑用下列类型的函数,计算误差平方和,并作图比较效果。
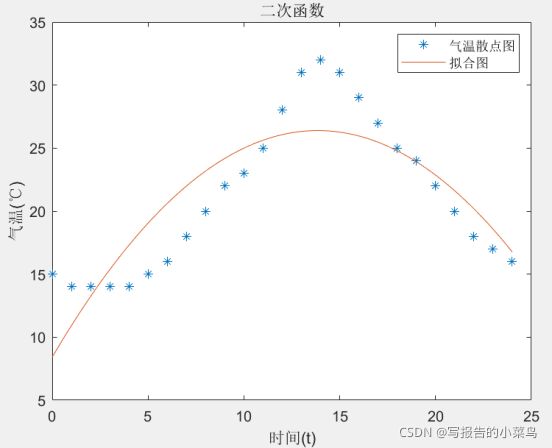
(1)二次函数
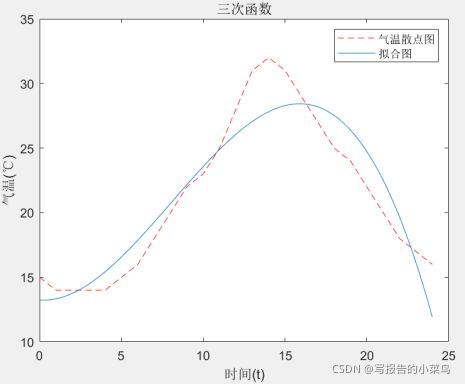
(2)三次函数
(3)四次函数
3 实验知识点
最小二乘法、非线性拟合
4 算法思想
所谓拟合是指已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别最小。拟合的方法除了最小二乘法外,还有拉格朗日插值法、牛顿插值法、牛顿迭代法、区间二分法、弦截法、雅克比迭代法和牛顿科特斯数值积分发等方法。
最小二乘拟合步骤:
2为最小,按ni=1这样的标准定义的bai拟合函数称为du最小二乘拟合,是离散情形下的最佳平方逼近.对给定数据点{(Xi,Yi)}(i=0,1,…,m),在取定的函数类Φ 中,求p(x)∈Φ ,使误差的平方和E2最小,E2=∑[p(Xi)-Yi]2。从几何意义上讲,就是寻求与给定点 {(Xi,Yi)}(i=0,1,…,m)的距离平方和为最小的曲线y=p(x)。函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
5 实验代码
5.1 二次函数
t=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
[p2,e2]=polyfit(t,y,2);
p=polyfit(t,log(y),2)
b=-p(1)
c=p(2)/(2*b)
a=exp(p(3)+b*c^2)
x1=0:0.1:24;
y2=polyval(p2,x1);
plot(t,y,'*',x1,y2)
xlabel('时间(t)');
ylabel('气温(℃)');
legend('气温散点图','拟合图');
title('二次函数');
e2
5.2 三次函数
t=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
[p3,e3]=polyfit(t,y,3);
p=polyfit(t,log(y),3)
b=-p(1)
c=p(2)/(2*b)
a=exp(p(3)+b*c^2)
x1=0:0.1:24;
y3=polyval(p3,x1);
plot(t,y,'r--',x1,y3)
xlabel('时间(t)');
ylabel('气温(℃)');
legend('气温散点图','拟合图');
title('三次函数');
e2
5.3 四次函数
t=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
[p4,e4]=polyfit(t,y,4);
p=polyfit(t,log(y),4)
b=-p(1)
c=p(2)/(2*b)
a=exp(p(4)+b*c^2)
x1=0:0.1:24;
y4=polyval(p3,x1);
plot(t,y,'r--',x1,y3)
xlabel('时间(t)');
ylabel('气温(℃)');
legend('气温散点图','拟合图');
title('四次函数');
e2
6.4 函数 ,式中a,b,c为常数(拟合参数)
,式中a,b,c为常数(拟合参数)
t=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
[p2,e2]=polyfit(t,y,2);[p3,e3]=polyfit(t,y,3);[p4,e4]=polyfit(t,y,4);
p=polyfit(t,log(y),2)
b=-p(1)
c=p(2)/(2*b)
a=exp(p(3)+b*c^2)
x1=0:0.1:24;
ye=a*exp(-b*(x1-c).^2);y5=a*exp(-b*(t-c).^2);e5=sqrt(sum((y-y5).^2));
plot(t,ye,'g-')
xlabel('时间(t)');ylabel('气温(℃)');legend('气温散点图','拟合图');
e2
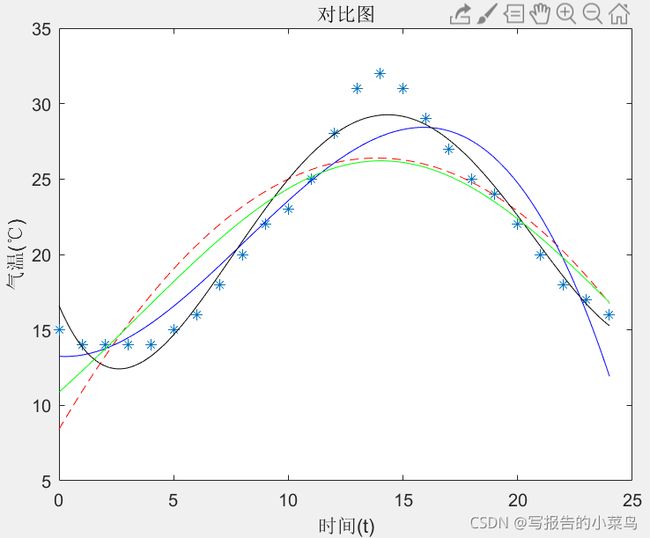
6.5 综合对比
t=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
[p2,e2]=polyfit(t,y,2);[p3,e3]=polyfit(t,y,3);[p4,e4]=polyfit(t,y,4);
p=polyfit(t,log(y),2)
b=-p(1)
c=p(2)/(2*b)
a=exp(p(3)+b*c^2)
x1=0:0.1:24;
y2=polyval(p2,x1);
y3=polyval(p3,x1);
y4=polyval(p4,x1);
ye=a*exp(-b*(x1-c).^2);y5=a*exp(-b*(t-c).^2);e5=sqrt(sum((y-y5).^2));
plot(t,y,'*',x1,y2,'r--',x1,y3,'b-',x1,y4,'k-',x1,ye,'g-')
xlabel('时间(t)');ylabel('气温(℃)');legend('气温散点图','拟合图');
title('二次函数');
e2