NEUQ-ACM week 2

T1:P2249 【深基13.例1】查找

题目描述

输入 n 个不超过 10^9 的单调不减的（就是后面的数字不小于前面的数字）非负整数 a1​,a2​,…,an​，然后进行 m次询问。对于每次询问，给出一个整数 q，要求输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 -1 。

输入格式

第一行 2个整数 n 和 m，表示数字个数和询问次数。

第二行 n 个整数，表示这些待查询的数字。

第三行 m 个整数，表示询问这些数字的编号，从 1 开始编号。

输出格式

输出一行，m个整数，以空格隔开，表示答案。

输入输出样例

输入 

11 3
1 3 3 3 5 7 9 11 13 15 15
1 3 6

输出 

1 2 -1 

说明/提示

数据保证，1 \leq n \leq 10^61≤n≤106，0 \leq a_i,q \leq 10^90≤ai​,q≤109，1 \leq m \leq 10^51≤m≤105

本题输入输出量较大，请使用较快的 IO 方式。

需要思考的问题

1.如何查找是都有这个数-二分法

2.若存在，如何快速找出第一次出现的位置-还是二分法（这个不容易想到）

（其实这题用lower_bound好像秒解）

思路

1.开一个数组存储数据

2.用二分法找是否存在目标值

3.若存在用二分法在它之前搜索第一次出现的位置

代码（注意二分法开闭区间和是否取等）

#include
using namespace std;
                 
long n,m,q;
int main()//p.s这题好像可以直接用lower_bound做
{
	cin>>n>>m;
	long arr[n];
	for(int i=0;i>arr[i];
	long  q;
	while(m>0)
	{
		cin>>q;
		long l=0,r=n;
		long mid;
		int b=-1;
		while(l<=r)//这里要取等(?)
		{
			mid=(l+r)/2;//第一次二分法求符合要求的一个元素
			if(arr[mid]==q)
			{
				if(mid>0&&arr[mid-1]==q)
				{
					long high=mid,low=0;
					while(lowq)r=mid-1;
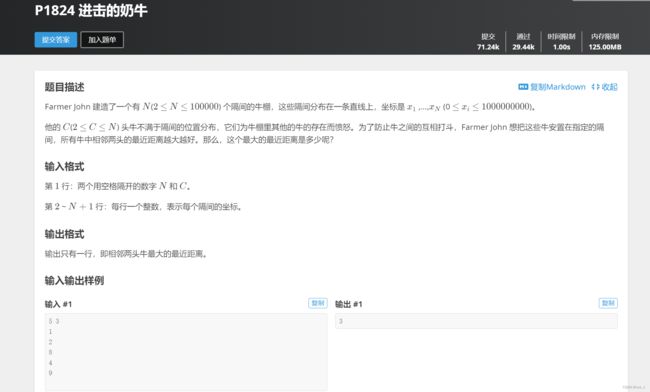
			else if(arr[mid]

T2.P1824 进击的奶牛

 需要思考的问题

1.''最大的最近距离'' --考虑二分法

2.怎么求这个距离（废话）

思路

1.先用数组初始化各个牛棚坐标

2.用二分法枚举可能的答案，编写函数判断这种情况是否成立（能不能装下所有牛）

代码

#include//用二分法枚举答案
using namespace std;
long arr[100001];
long n,c,mid;
long ans=0;
bool check(long m)//检查当距离为mid时符不符合要求
{
	
		long cnt=0;//实际能装几头牛
		long d;
		long l=arr[0];//初始化隔间为arr[0]
		for(int i=1;i=m)//如果两个相邻隔间距离大于m就符合要求
			{
				cnt++;
				l=arr[i];//更新隔间号
			}
		}
		if(cnt>=c-1)return true;//实际能装的比需要的多就符合题意
		else return false;
	
	
}

int main()
{
	cin>>n>>c;
	for(int i=0;i>arr[i];
	sort(arr,arr+n);//用二分法之前先排序
	long l=arr[0],r=arr[n-1];//为啥不能l=0，r=n-1??
	while(l<=r)//二分法
	{
		long mid=(l+r)/2;
		if(check(mid))
		{
			ans=mid;
			l=mid+1;
		}
		else r=mid-1;
	}
	cout<

T3.P2678 [NOIP2015 提高组] 跳石头

 需要思考的问题

1.如何初始化数组（注意起点和终点不参与运算）

2.如何判断要搬几块石头（贪心）

思路

1.建立数组输入数据，注意输入要从数组第二号位开始，且终点要单独再输一次

2.用二分法枚举答案

3.check函数：假设每一步都要符合距离，则石头间距不够的话就挪，最后算挪了多少个

代码

#include
using namespace std;
int d,n,m;
const int N = 5 * 1e5 + 10;
int arr[N];
bool check(int u)
{
    int cnt=0;//搬走的石头总数
    int nex=0;//下一步将要去哪
    int cur=0;//目前位置
    while(nexm)return false;//搬走的石头不能超过给的m
     return true;
}


int main()
{
    int ans;
    cin>>d>>n>>m;
    for(int i = 1; i <= n; i ++) cin>>arr[i];//注意要从1开始，因为arr[0]不能搬走（不参与函数运算）
    arr[n+1] = d;//把终点放到数组里 
    int l = 0,r = d;
    while(l<=r)//典型二分法（注意l可等于r）
    {
      int mid = (l + r )/2;
        if(check(mid)) 
        {
            l=mid+1;
            ans = mid;
            
        }
        else r = mid - 1;
    }
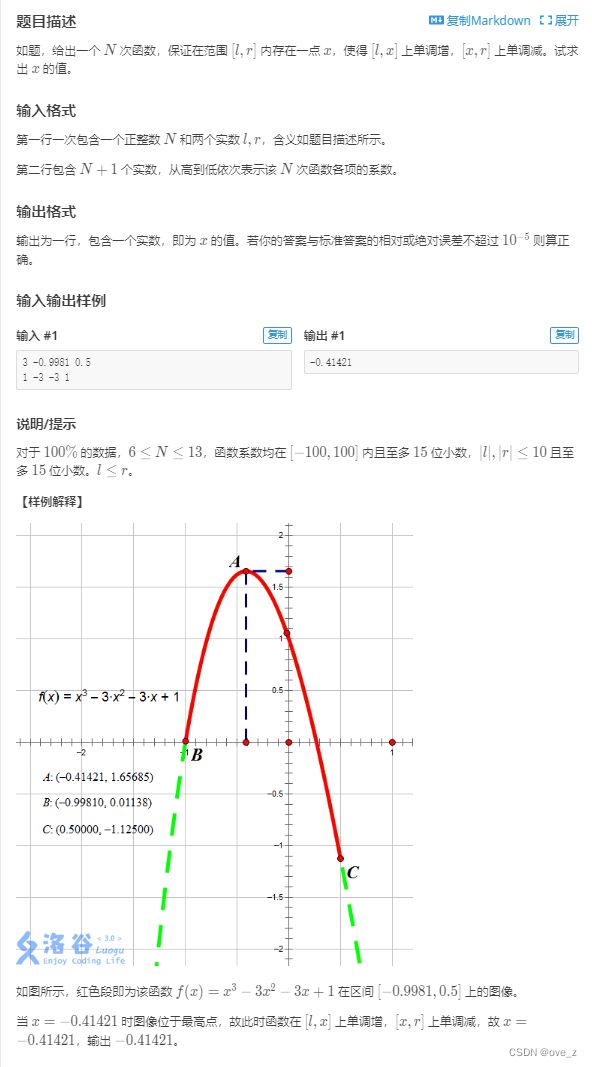
    cout<

T4.P1024 [NOIP2001 提高组] 一元三次方程求解

需要思考的问题

1.怎么判断根的位置（零点存在性定理+二分）

2.怎么在遍历区间同时确定根的位置

思路

1.初始化数据，编一个函数算出x对应的y

2.先在长度为1的区间一个一个查找，有零点再用二分法逼近

代码

#include//完全没用到二分法的一种解
using namespace std;
double a,b,c,d;
double ans[3];
int main()
{
    cin>>a>>b>>c>>d;
    int i=0;
    for(double x=-100;x<=100;x+=0.01)
    {
        if((a*x*x*x+b*x*x+c*x+d)*(a*(x+0.01)*(x+0.01)*(x+0.01)+b*(x+0.01)*(x+0.01)+c*(x+0.01)+d)<0)
        {
            ans[i]=x+0.01;
            i++;
        }
        
    }
    sort(ans,ans+3);
    for(int i=0;i<3;i++)cout<
using namespace std;
double a,b,c,d;
double check(double x)//算出对应的y
{
    double y;
    y=a*x*x*x+b*x*x+c*x+d;
    return y;
}

int main()
{
    cin>>a>>b>>c>>d;
    for(int i=-100;i<100;i++)
    {
        double l=i,r=(i+1);
        double mid;
        if(check(l)==0)cout<=0.001)//注意精度设置，保留两位小数要差值小于0.01
            {
                mid=(l+r)/2;//开始二分
                if(check(mid)*check(l)<=0)r=mid;
                else l=mid;
            }
            cout<

T5.P3382 【模板】三分法

需要思考的问题

1.怎么用三分法

代码（还不是很理解原理）

#include 
using namespace std;
#define epx 1e-7
double a[100];
double n,l,r,midl,midr;
double f(double x)
{
    double num=0;
    for(int i=0;i<=n;i++)
        num+=a[i]*pow(x,n-i);//算出x对应的y
    return num;
}
int main()
{
    cin>>n>>l>>r;
    for(int i=0;i<=n;i++)
        cin>>a[i];
     while(fabs(r-l)>=epx)//三分法的精髓
    {
        midl=l+(r-l)/3.0;
        midr=r-(r-l)/3.0;
        if(f(midl)>f(midr))
        r=midr;
        else
        l=midl;
    }//三分法的精髓
    cout<