NEUQ-ACM week4
7-1 Lily
需要思考的问题
这题比较简单,唯一要考虑的可能就是怎么在摆放c的时候不覆盖掉已经有的l
思路
1.创建字符串,读取数据
2.从头到尾遍历,是l的地方就先输出l
3.对于是‘ . ’的地方先判断前后有没有l,如果前后都没有l就可以放c,否则按‘ . ’输出。
代码
#include
using namespace std;
string str;
int arr[1005];
int main()
{
int n;
cin>>n;//感觉这步没啥用
cin>>str;
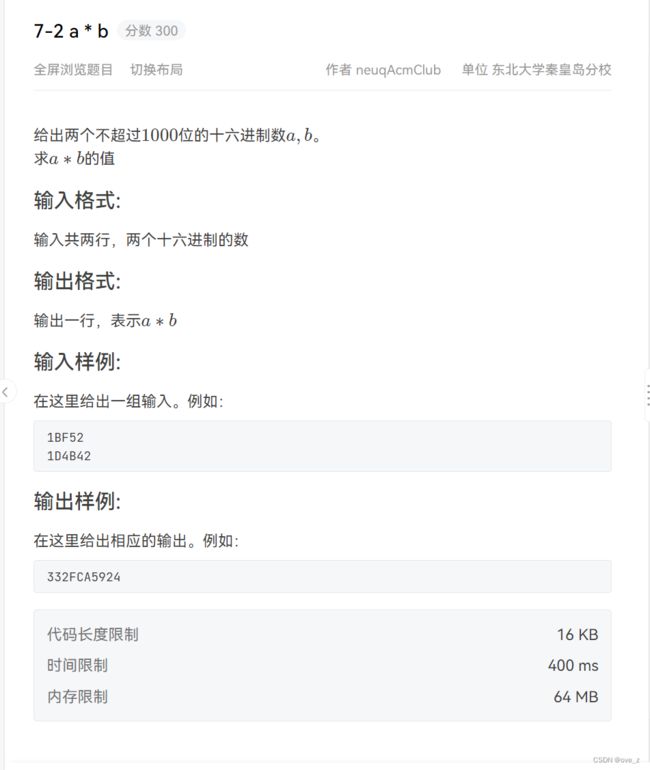
for(int i=0;i 7-2 a x b
需要思考的问题
1.十六进制怎么表示9以上的位
2.十六进制乘法进位怎么实现
3.乘完的数字怎么变回十六进制再输出
思路
1.开三个数组,两个用来存乘数
2.倒序,顺便把a~f这几个字母asc码-7,使得a相当于10的asc码+1,以此类推
3.高精度乘法(之前有讲过)
4.同样的方法把10~15变成字母a~f
5.删除前导0,输出
代码
#include
using namespace std;
char a1[1000],b1[1000],c1[10000];
int a[1000],b[1000],c[100000];
int main()
{
cin>>a1>>b1;
int lena,lenb;
lena=strlen(a1);
lenb=strlen(b1);
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));//初始化数据
for(int i=1;i<=lena;i++)
{
if(a1[lena-i]>='A'&&a1[lena-i]<='Z')a[i]=a1[lena-i]-'7';//碰到字母用asc码转化成数字
else a[i]=a1[lena-i]-'0';
}
for(int i=1;i<=lenb;i++)
{
if(b1[lenb-i]>='A'&&b1[lenb-i]<='Z')b[i]=b1[lenb-i]-'7';//碰到字母用asc码转化成数字
else b[i]=b1[lenb-i]-'0';
}
int temp;
for(int i=1;i<=lena;i++)
{
for(int j=1;j<=lenb;j++)
{
c[i+j-1]+=a[i]*b[j];
c[i+j]+=c[i+j-1]/16;
c[i+j-1]%=16;//高精度乘法(注意是十六进制所以除的是16)
}
}
int lenc=lena+lenb;
while(c[lenc]==0&&lenc>=1)lenc--;//删除前导0
for(int i=1;i<=lenc;i++)
{
if(c[i]>=10&&c[i]<=15)c1[i]=c[i]+'7';
else c1[i]=c[i]+'0';
}
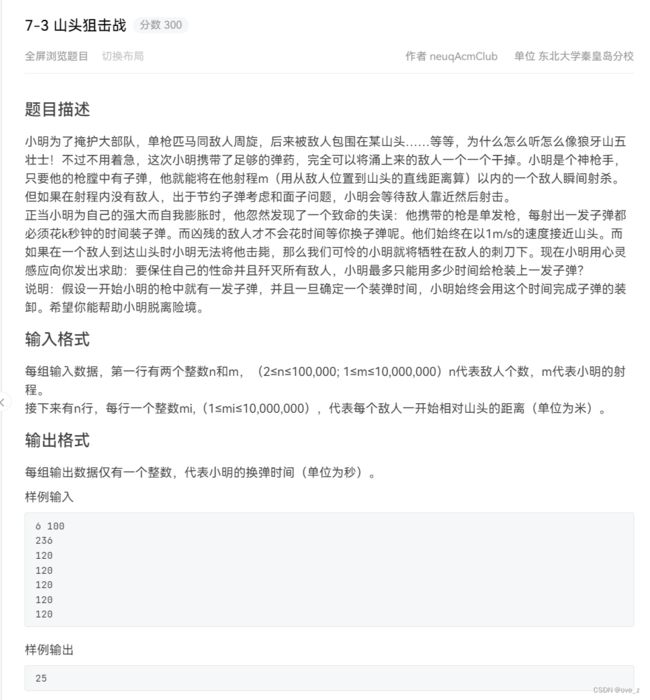
for(int i=lenc;i>=1;i--)cout< 7-3 山头狙击战
需要思考的问题
1.怎么表示每个敌人的位置(因为被杀掉可以相当于把这个元素扔掉了,所以考虑队列处理)
2.敌人一直在移动,怎么把动态的问题转化成静态的处理(感觉这个是难点)
3.怎么求最大换弹时间(二分法遍历答案,但是这题似乎可以不用)
思路
1.先假设小明不会死,等他杀完全部敌人之后看离他最远的那个敌人再这段时间走过的路程和最远敌人一开始距离小明的距离,如果走过的路大于距离说明在被杀之前已经到达小明身边,此时小明失败
2.遍历答案,把可能的答案用1)的思想判断是否可行,当第一次出现不可行的情况说明上一种情况就是最大值
代码
#include
using namespace std;
const long Max=1e7;
long arr[Max];
long n,m;
queueenemy;//用队列处理(栈应该也可以)
bool check(int x)//x就是换弹时间
{
long cnt=0;//统计总路程
int win=1;//标识符,失败置为0
for(int i=0;im)//第一个敌人单独考虑
cnt+=enemy.front()-m;
enemy.pop();
while(win)
{
cnt+=x;//换弹
if(enemy.front()-cnt<0)
{
win=0;
break;
} //代表敌人已经到达,失败
if(enemy.front()-cnt>m)//如果换完弹后理他最近的敌人还没进入射程
{
long time=enemy.front()-cnt-m;//等到最近的敌人刚刚进入射程花费的时间
cnt+=time;//把等待时间加到总时间里
enemy.pop();//击杀
}
else//这个时候射程范围内已经有敌人
{
enemy.pop();//击杀距离他最近的敌人
}
if(enemy.empty())break;
}
while(!enemy.empty())enemy.pop();//一定要记得每次判断完要清空队列
if(win==0)return false;
else return true;
}
int main()
{
int ans;
cin>>n>>m;
for(int i=0;i>arr[i];
sort(arr,arr+n);//排序,方便比较
for(int i=1;;i++)//这里也可以用二分法()
{
if(check(i))
ans=i;
else break;//只要一次不符合就能判定上一个是最大时间
}
cout< 7-5一元三次方程
需要思考的地方
肯定要二分查找,但怎么在不知道单调性的情况下用二分法
思路
求出导函数两个零点,两个零点把函数分成三个单调的区间,在这三个单调区间之内用二分法
代码
#include
using namespace std;
int n;
const double eps=1e-6;
double a,b,c,d,p,q;
double x1,x2;
double f(double x)//算出x对应的y
{
double y=a*x*x*x+b*x*x+c*x+d;
return y;
}
double find(double l,double r)//二分查找
{
double mid=(l+r)/2;
while(fabs(f(mid)) > eps)//不论递增递减都可以
{
if(f(mid)*f(r)>0)r=mid;//mid和r在同一侧,所以r缩到mid
if(f(mid)*f(l)>0)l=mid;//mid和l在同一侧,所以l增到mid
mid=(l+r)/2;//注意要更新mid
}
return mid;
}
int main()
{
cin>>n;
for(int i=0;i>a>>b>>c>>d>>p>>q;
x1=(-b-sqrt(b*b-3*a*c))/(3*a);//找出两个极值点,分成三段单调的区间
x2=(-b+sqrt(b*b-3*a*c))/(3*a);
if(x1>x2)swap(x1,x2);//保证总小到大的区间查找顺序
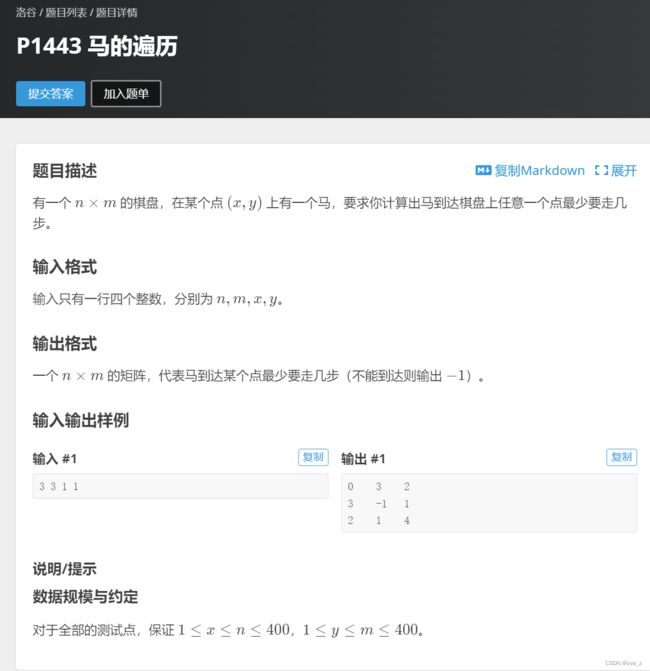
cout< p1443 马的遍历
需要思考的问题
1.最重要的,bfs怎么用
2.用什么数据结构可以一个数据对应两个坐标(pair)
思路
1.初始化数据,用pair类型的队列存储
2.bfs搜索
代码
#include
using namespace std;
int n,m,x,y;
int direction_x[8]={-1,-2,-2,-1,1,2,2,1};//总所周知马走日
int direction_y[8]={2,1,-1,-2,2,1,-1,-2};
queue >q;//bfs用队列实现
int step[400][400];//存步数
bool vis[400][400];//这个点是否走过
int main()
{
cin>>n>>m>>x>>y;
memset(vis,false,sizeof(vis));//先全部初始化为没经过
memset(step,-1,sizeof(step));
step[x][y]=0;//设置起点为第零步
vis[x][y]=true;//把起点标记为已经走过的状态
q.push(make_pair(x,y));//pair真好用
while(!q.empty())//只要队列非空就说明能扩展到其他的点,就一直做循环
{
int x_first=q.front().first;
int y_first=q.front().second;//取出队首并出队
q.pop();
for(int i=0;i<8;i++)//遍历所有可能状态
{
int x_next=x_first+direction_x[i];
int y_next=y_first+direction_y[i];
if(x_next<1||x_next>n||y_next<1||y_next>m||vis[x_next][y_next])continue;//边界条件不满足就说明走不通,跳过
vis[x_next][y_next]=true;//把后一个点标记为走过
q.push(make_pair(x_next,y_next));//把这个点加入队列中
step[x_next][y_next]=step[x_first][y_first]+1;//相当于是一个递推关系
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cout< P1605 迷宫
需要思考的地方
经典dfs题目~就是需要知道dfs怎么实现的。
代码
#include
using namespace std;
int m,n,t;
int sx,sy,fx,fy;
int ans=0;
int mp[10][5]={0};//整体地图,先把每个点都初始化为零
int plus_x[4]={1,-1,0,0},plus_y[4]={0,0,1,-1};//下一步可能的四个状态
bool flag[10][10]={false};//判断某个点是否到达过
bool judge(int x,int y)//判断这个点是否符合要求
{
if(x<1||x>n||y<1||y>m)return false;//越界
if(mp[x][y]==1||flag[x][y]==true)return false;//这个状态之前走过
return true;//否则就可以走
}
void dfs(int x,int y)
{
if(x==fx&&y==fy)//到达终点
{
ans++;
return;//话说这个return到底是啥意思捏
}
flag[x][y]=true;//先标记为没走过
for(int i=0;i<4;i++)//遍历下个状态所有可能情况
{
int next_x,next_y;
next_x=x+plus_x[i];
next_y=y+plus_y[i];
if(judge(next_x,next_y))//判断这个情况是否可行
{
dfs(next_x,next_y);//对下个状态dfs
flag[next_x][next_y]=false;//回溯
}
}
}
int main()
{
cin>>m>>n>>t;//长 宽 障碍数
cin>>sx>>sy>>fx>>fy;//起点坐标和终点坐标
for(int i=0;i>x>>y;
mp[x][y]=1;//有障碍的话就置为1
}
dfs(sx,sy);//从起点开始dfs
cout< 这周学dfs和bfs,感觉对其中的回溯过程一直不太清楚到底是怎么通过代码一步步实现的,具体地说,明白回溯的目的和比较宏观的解释(退回上一个状态)但是具体的代码一步步的推导还是不太行。目前似乎只能根据模板来写题,看来还需多练习呀~