NEUQ-ACM week 6

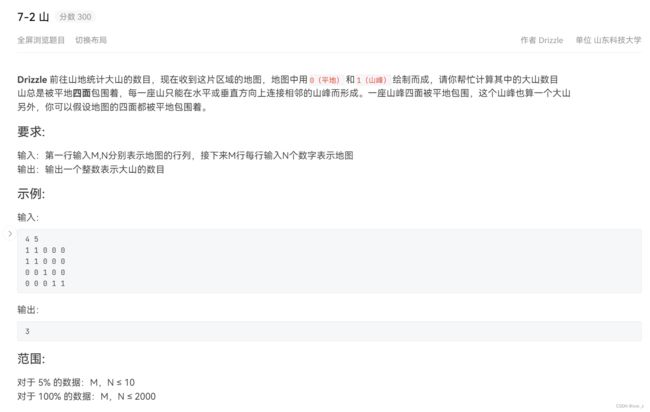
T1 7-2 山

 需要思考的问题

1.bfs裸题，相当于搜索连通块个数

2.这种有带坐标的题目基本可以用pair做

代码

#include
using namespace std;
int m,n,ans=0;
int mp[2005][2005]={0};
bool vis[2005][2005];
int x_plus[4]={1,0,0,-1};
int y_plus[4]={0,1,-1,0};
queue >q;
int main()
{
    memset(vis,false,sizeof(vis));
    cin>>m>>n;
    for(int i=0;i>mp[i][j];//初始化地图
    }

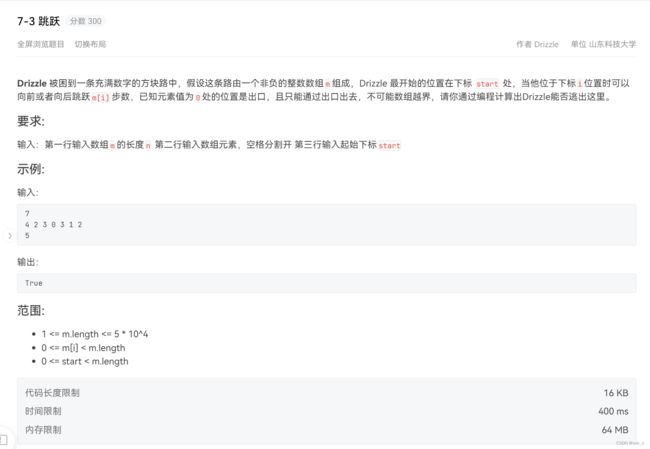
    for(int i=0;i=0&&x_next=0&&y_next

T2.7-3 跳跃

需要思考的问题

类似于上周做的奇怪的电梯，都是比较简单的dfs

代码

#include
using namespace std;
const int N=5*1e4;
int n,start,flag=0;
int m[N];
bool vis[N];
void dfs(int x)
{
    if(m[x]==0)flag=1;
    vis[x]=true;
    for(int i=1;i>=-1;i-=2)
    {
        int next=x+i*m[x];
        if(vis[next]==false&&next>=0&&next>n;
    for(int i=0;i>m[i];
    cin>>start;
    dfs(start);
    if(flag)cout<<"True";
    else cout<<"False";
   
}

T3.p1007 独木桥

需要思考的问题

1.怎么把两个士兵碰在一起然后分别回头这一过程转化成代码--其实只要假设他们穿过彼此

2.最大时间和最小时间分别代表着什么--最大时间，最后面士兵走到离桥最远的一端 最小时间-最中间士兵从远端离开桥

思路

1.先初始化每个士兵的位置坐标

2.再求出最大和最小值

代码

#include
using namespace std;
int main()
{
    int Max=0,Min=0;
    int l,n;
    cin>>l>>n;
    for(int i=0;i>m;
        Max=max(Max,max(l-m+1,m));
        Min=max(Min,min(l-m+1,m));//精髓
    }
    cout<

T4.P1090 [NOIP2004 提高组] 合并果子 

需要思考的问题

就是尽量优先选取总重量小的两堆果子来合并，用优先队列实现

思路

1.声明优先队列，把每一堆果子重量入列

2.把队列前两个取出来加和，再把加和后的重量入列，同时ans加上这个数

代码

#include
using namespace std;
priority_queue,greater >q;//优先队列声明
int n,weight,ans;
int main()
{
    cin>>n;
    for(int i=0;i>weight;
        q.push(weight);
    }   
    while(q.size()>=2)
    {
        int a=q.top();
        q.pop();
        int b=q.top();
        q.pop();
        ans+=(a+b);
        q.push(a+b);
    }
    cout<

 T5.P1223 排队接水

需要思考的问题

一眼贪心

思路

1.用两个数组一个存序号一个存用时

2.对每个人用时以及对应序号升序排列，此时这个顺序就是最小时间

3.算出答案，即每个人等待时间➗总人数

#include
using namespace std;
int arr[1005],num[1005];
int n;
double sum=0;
int main()
{
    cin>>n;
    for(int i=0;i>arr[i];
        num[i]=i+1;
    }
    for(int i=0;iarr[j])
            {
                int k=arr[i];
                arr[i]=arr[j];
                arr[j]=k;
                int x=num[i];
                num[i]=num[j];
                num[j]=x;
            }
        }
    }
    for(int i=0;i

T6.P1199 [NOIP2010 普及组] 三国游戏

需要思考的问题

由题目可知小涵和电脑都拿不到每个武将的最大默契值，因为小涵每拿起最大组合的其中一个，另一个就被电脑拿走了，但是电脑也无法占有该组合的最大值，因为另一个在小涵手里，这个组合的最大值其实就作废了。但是小涵在第二次选将时可以拿到第一次选中的武将的次大默契值组合。在双方都拿不到最大默契值的情况下，显然谁拿到次大默契组合的最大值，谁就赢了。

思路

1.先开一个二维数组，对称的初始化每个武将的默契值

2.对每行进行升序排列

3.选出表格里最大的默契值和次大的默契值配对即可

#include
using namespace std;
int a[505][505];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i>a[i][j];
            a[j][i]=a[i][j];
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        sort(a[i]+1,a[i]+1+n);
        if(a[i][n-1]>ans) ans=a[i][n-1];
                
    }
    cout<<'1'<