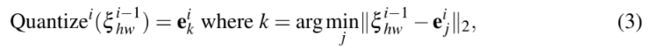BMVC2022 | HR-VQVAE：用于图像重建和生成的基于Hierarchical Residual Learning的VQVAE

原文标题：Hierarchical Residual Learning Based Vector Quantized Variational Autoencoder for Image Reconstruction and Generation

链接：https://bmvc2022.mpi-inf.mpg.de/0636_poster.pdf

paper：https://arxiv.org/abs/2208.04554

一、问题提出

离散的潜在变量允许使用强大的自回归模型，以避免后验崩溃问题。此外，该模型可以大大减少重建图像所需的信息量。然而，VQVAE存在码本崩溃的问题：在训练过程中的某个时刻，码本的某些部分可能不再使用，模型不再使用离散表示的全部容量，导致重建效果不佳。此外，k-means问题随着质心的增加变得更加严重，用大量离散编码编码输入的能力降低了

VQVAE2通过采用多层量化表示(如顶层、中层和底层)来处理图像中的分层信息，对VQVAE进行了扩展，然后，使用两个自回归卷积网络分别对结构信息和纹理信息进行建模，生成新的图像。然而，不同的层共享相同的目标函数。这并不鼓励层对互补信息进行编码，并导致codebook的低效使用。

二、模型方法

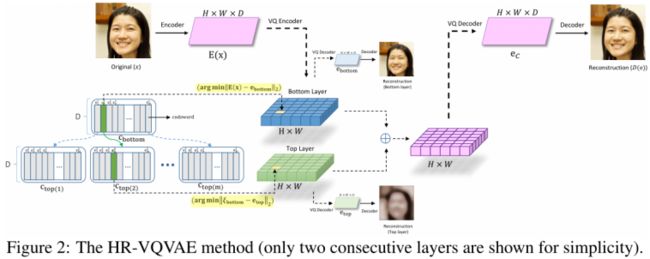
与VQVAE不同的是，embedding随后被迭代量化为n个离散潜在变量的层。假设第一层有一个大小为m的码本，第二层将有m个大小为m的码本，以此类推，第i层有m^(i-1)个大小为m的codebook，总共有m^i个code。

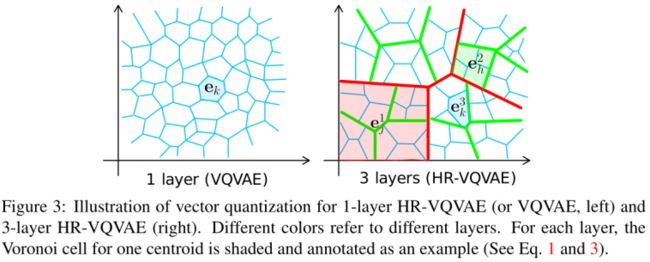
这种分层搜索过程提供了本地访问码本索引的优势，极大地减少了搜索时间（可类比于操作系统中的分页搜索）：

在每i层中，对码本进行优化：

使用哪个codebook是由前一层选择的code et决定的。在每层，将code组合成张量ei∈R(H×W×D)。然后，在不同的层中，将张量ei组合在一起，形成“组合”离散表示eC，反过来，它被feed到解码器中，重建图像x：

目标函数为：

使用自回归模型(PixelCNN)将先验分布拟合到所有训练样本中。这样的模型将输入空间上的联合概率分布分解为样本每个维度的条件分布的乘积。对于新图像的生成，使用ancestral采样，利用概率的链式法则。

三、实验

1、dataset

FFHQ(256 × 256)， ImageNet(128 × 128)， CIFAR10(32 × 32)、MNIST(28 × 28)

2、实验

1）层数

定义n层模型，每个码本有m个码字。为确保模型之间的分辨率水平相同，在最后一层中比较具有相同数量code的模型，即最大的像素值。

在最后一层都有64个码字，但我们观察到，增加模型的深度会导致更多细节的重建：

codebook的分层性质在训练过程中起到了正则化的作用，并允许模型更有效地分配code。

与VQVAE-2比较了模型深度(即层数)对重构均方误差(MSE)的影响：

增加模型层数可以提高HR-VQVAE的性能。此外，HR-VQVAE在所有数据集上的性能都随着层数的增加而不断提高。然而，增加层数并不能从一定程度上提高VQVAE-2的性能(对于Imagenet和FFHQ)，在某些情况下(MNIST和CIFAR10)，性能下降。

2）codebook大小

增加码本大小以及VQVAE和VQVAE-2的效果：

不同数据集和方法的平均MSE与码字数。当码本大小增加到一定限度时，VQV AE和VQV AE-2都会崩溃。然而，HR-VQVAE继续改善。

重建过程：

VQV AE和VQV AE-2都受到codebook崩塌的影响。相反，HR-VQVAE可以充分利用增加的复杂性，并生成最佳重建。

3）每层codebook的效果

3层HR-VQVAE和3层VQVAE-2，说明了两种模型中不同层编码的不同信息：

HR-VQVAE图像重建(第一行)比VQVAE-2(第二行)获得了更好的重建质量和更多的细节。一种可能的解释是HR-VQVAE鼓励不同的层对图像的不同信息进行编码;而VQVAE-2中的信息是大量重叠的。这可能导致低效率的潜在表示。

HR-VQVAE, VQV AE, VQVAE-2图像重建的均方误差(MSE)和fréchet初始距离(FID)：

重建速度：

HR-VQV AE和VQV AE-2生成的随机样本：

其实这篇文章创新度是有限的，显然将VQVAE2改成更多层是一个很自然的想法吧。