《FCOS：Fully Convolutional One-Stage Object Detection》论文笔记

代码地址：FCOS

1. 概述

导读：这篇文章使用类似语义分割的方法提出了一个全卷积一阶段检测器（FCOS），该检测器是anchor-free的，因而就避免了那些经典anchor检测器需要的复杂计算与内存资源（IoU计算）以及对应的参数，最后的检测结果只需要经过NMS即可输出检测结果。该网络结构通过每个前景像素上在预测一个4维的向量$(l,t,r,b)$来确定检测框。

下面图1中左图展示了FCOS的检测表达，由图展示的是同一个位置无法明确确定那个检测框需要用于回归，文章后面通过一定的策略（最小面积选择）与多尺度预测缓解。

尽管基于anchor的检测器在实际使用中已经取得了一些成功的案例，但是同时也是存在如下的一些缺点：

• 1）检测的结果对anchor的scale、ratio以及数量比较敏感。比如在RetinaNet中这些参数能够在COCO数据集上体现出4%的差别。所以这些参数需要精心设计才可以；
• 2）即使这些参数被很好设计出来了，但是这些参数在设计出来的时候就被定死了，这个限制了检测器的扩展性（遇到新的问题就需要重新设计），并且对于小目标检测存在难度；
• 3）一般为了取得较高的召回率，会将anchor的个数设置得很大，这就导致了很多的anchor都是负样本，从而正负样本的比例极不平衡；
• 4）如此多数量的anchor也会显著增加计算量与内存资源；

这篇文章的方法能够达到传统上使用anchor的检测算法精度，其中为了抑制距离目标中心较远预测质量差的问题引入center-ness分支，它预测一个像素距离边界框中心的偏移。它的score用于降低这些低质量框的权重并在NMS中被合并。

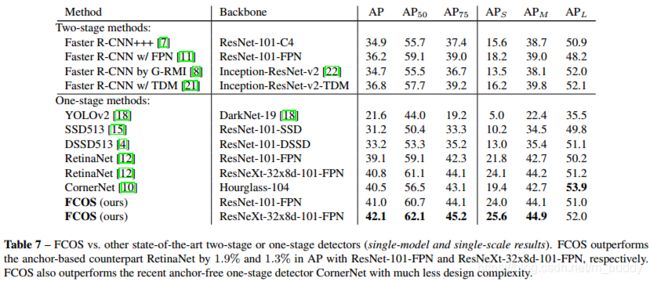
这篇文章提出的方法具有如下的优点：

• 1）使用这篇文章的方法应将检测与其它的全卷积解决的任务联合起来了，因而就可以使用诸如语义分割中的方法来优化检测；
• 2）由于是anchor-free的就排除了前面提到的由anchor带来的一些列问题；
• 3）文章提出了state-of-art的一阶段检测算法FCOS，这个算法可用于替换掉两阶段检测算法中的RPN网络，这样产生的结果将更好；
• 4）这篇文章提出的方法可以通过少量的更改就可以直接被用于其它视觉任务中，诸如实例分割与关键点检测；

2. 方法设计

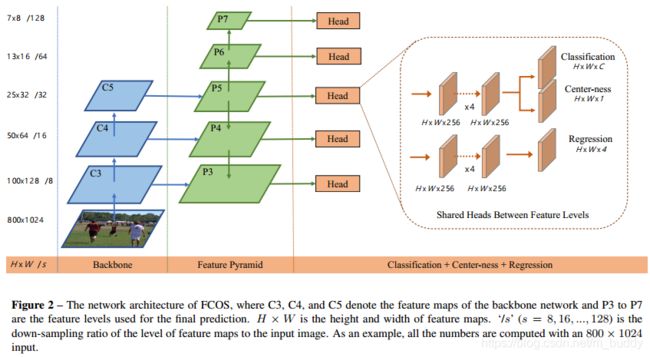
2.1 网络结构

2.2 全卷积一阶段检测器

杜宇来自backbone第$i$层的特征表示为$F_i$，对于GT表是为$B_i=(x_0^{(i)},y_0^{(i)},x_1^{(i)},y_1^{(i)},c^{(i)})$，分别表示左上与右下两个坐标及分类的类别。对于该特征图上坐标为$(x,y)$的点，其对应到原图区域的中心点为$(\frac{s}{2}+xs,\frac{s}{2}+ys)$。

在anchor-based的检测算法中将anchor的中心当做目标的位置，并回归与之对应的参数。但是在这篇文章是直接在每个特征图的点上回归检测框，这样的机制有点类似于语义分割，逐像素进行的。

位于位置$(x,y)$处的采样被划归为正样本的条件是其匹配到任意一个GT并且分类类别不为背景。对于网络的回归目标$t^{\ast }=(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，这几个东西分别表示采样点与检测框四个边界的距离。对于一个采样点可能对应多个重叠较多的目标的时候，图1中右图所示，这里是选取当前采样点最小面积的区域作为回归的目标，则对应的回归目标可以描述为：

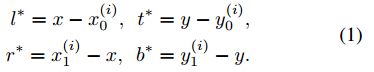
PS： anchor-based方法只选用IoU最高的anchor去进行回归，而在FCOS中是选用尽可能多的前景采样去回归，这是文章中认为好于对应的anchor-based检测器的原因。

网络输出：
网络的输出包含一个分类向量$p$，与4维的坐标回归参数（相比anchor-based方法，并不会随着anchor增加而计算量加大）。

损失函数：
损失函数与一般的检测方法损失函数类似，也是采用分类损失加上边界框回归损失的形式：

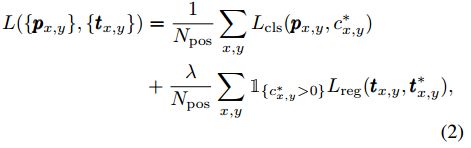
其中，对于分类损失是使用focal loss，而边界框的回归损失采用的是IoU loss。

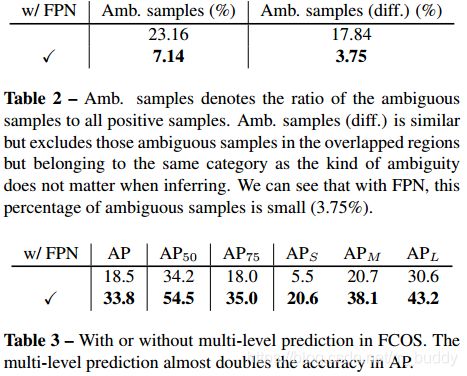
2.3 FCOS使用FPN进行多尺度预测

文中提到多尺度预测会为文章的方法带来两个方面的好处：1）提供更好的召回率；2）缓解前文提到的检测框归属模糊问题（规定各层回归尺度缓解）；

在FPN的检测网络中，基于anchor的检测器会按照anchor的大小将生成的anchor boxes分配到不同尺度的特征图上，从而提升检测的精度。这篇文章的方法也有类似的机制，只不过是直接指定的，由$m_i$确定。既是满足$max(l^{\ast },t^{\ast },r^{\ast },b^{\ast }>m_i)ormax(l^{\ast },t^{\ast },r^{\ast },b^{\ast }<m_{i-1})$，其中$m_2,m_3,m_4,m_5,m_6,m_7$的取值分别为$0,64,128,256,512,\infty$（个人觉得有些问题，后序看看代码具体怎么写的-_-||）。

FPN对于模糊目标与性能的影响见表2与表3所示：

2.4 FCOS中的Center-ness

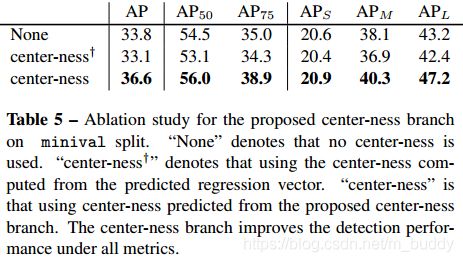
在FPN检测结果的基础上，文章发现由于一些低质量的预测框导致文章算法差于对应的一阶段检测器，这些低质量的检测框主要由定位远离目标中心导致的，对此文章提出了一个有效且不需要任何参数的应对策略Center-ness来进行抑制，这部分工作由与分类相平行的分支来进行预测，对应的预测结果与分类置信度相乘用于最后筛选检测结果。
对于Center-ness预测GT的标注文章写得比较简略，只是给定一个对于一个位置的回归目标其Center-ness的计算过程：

以及一个Center-ness的示意图：

采用的损失函数是binary交叉熵损失函数，这个损失会加入到公式2中一起参与训练。（具体怎么生成Center-ness标注的需要对照源码-_-||）
Center-ness对性能带来的影响见表5所示：

3. 实验结果