deeplearning.ai课程作业:Course 1 Week 2
deeplearning.ai课程作业:Course 1 Week 2
原始作业在GitHub上下载,本文仅作为本人学习过程的记录,含答案,不喜勿看。全部自己跑过,保证可行。
Part 1:Python Basics with Numpy (optional assignment)
Welcome to your first assignment. This exercise gives you a brief introduction to Python. Even if you’ve used Python before, this will help familiarize you with functions we’ll need.
Instructions:
- You will be using Python 3.
- Avoid using for-loops and while-loops, unless you are explicitly told to do so.
- Do not modify the (# GRADED FUNCTION [function name]) comment in some cells. Your work would not be graded if you change this. Each cell containing that comment should only contain one function.
- After coding your function, run the cell right below it to check if your result is correct.
After this assignment you will:
- Be able to use iPython Notebooks
- Be able to use numpy functions and numpy matrix/vector operations
- Understand the concept of “broadcasting”
- Be able to vectorize code
Let’s get started!
About iPython Notebooks
iPython Notebooks are interactive coding environments embedded in a webpage. You will be using iPython notebooks in this class. You only need to write code between the ### START CODE HERE ### and ### END CODE HERE ### comments. After writing your code, you can run the cell by either pressing “SHIFT”+”ENTER” or by clicking on “Run Cell” (denoted by a play symbol) in the upper bar of the notebook.
We will often specify “(≈ X lines of code)” in the comments to tell you about how much code you need to write. It is just a rough estimate, so don’t feel bad if your code is longer or shorter.
Exercise: Set test to “Hello World” in the cell below to print “Hello World” and run the two cells below.
### START CODE HERE ### (≈ 1 line of code)
test = "Hello World"
### END CODE HERE ###
print ("test: " + test)
test: Hello World
Expected output:
test: Hello World
What you need to remember:
- Run your cells using SHIFT+ENTER (or “Run cell”)
- Write code in the designated areas using Python 3 only
- Do not modify the code outside of the designated areas
1 - Building basic functions with numpy
Numpy is the main package for scientific computing in Python. It is maintained by a large community (www.numpy.org). In this exercise you will learn several key numpy functions such as np.exp, np.log, and np.reshape. You will need to know how to use these functions for future assignments.
1.1 - sigmoid function, np.exp()
Exercise: Build a function that returns the sigmoid of a real number x. Use math.exp(x) for the exponential function.
Reminder:
sigmoid(x)=11+e−xsigmoid(x)=11+e−x is sometimes also known as the logistic function. It is a non-linear function used not only in Machine Learning (Logistic Regression), but also in Deep Learning.
To refer to a function belonging to a specific package you could call it using package_name.function(). Run the code below to see an example with math.exp().
# GRADED FUNCTION: basic_sigmoid
import math
def basic_sigmoid(x):
"""
Compute sigmoid of x.
Arguments:
x -- A scalar
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1 / (1 + 1/ math.exp(x))
### END CODE HERE ###
return s
basic_sigmoid(3)
0.9525741268224334
Expected Output:
| Input | Output |
|---|---|
| basic_sigmoid(3) | 0.9525741268224334 |
Actually, we rarely use the “math” library in deep learning because the inputs of the functions are real numbers. In deep learning we mostly use matrices and vectors. This is why numpy is more useful.
### One reason why we use "numpy" instead of "math" in Deep Learning ###
x = [1, 2, 3]
basic_sigmoid(x) # you will see this give an error when you run it, because x is a vector.
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
in ()
1 ### One reason why we use "numpy" instead of "math" in Deep Learning ###
2 x = [1, 2, 3]
----> 3 basic_sigmoid(x) # you will see this give an error when you run it, because x is a vector.
in basic_sigmoid(x)
15
16 ### START CODE HERE ### (≈ 1 line of code)
---> 17 s = 1.0 / (1 + 1/ math.exp(x))
18 ### END CODE HERE ###
19
TypeError: a float is required
In fact, if x = ( x 1 , x 2 , . . . , x n ) x = ( x 1 , x 2 , . . . , x n ) \ x=(x_1,x_2,...,x_n)x=(x_1,x_2,...,x_n) x=(x1,x2,...,xn)x=(x1,x2,...,xn) is a row vector then np.exp(x)np.exp(x) will apply the exponential function to every element of x. The output will thus be: n p . e x p ( x ) = ( e x 1 , e x 2 , . . . , e x n ) \ np.exp(x)=(e^{x_1},e^{x_2},...,e^{x_n}) np.exp(x)=(ex1,ex2,...,exn)
import numpy as np
# example of np.exp
x = np.array([1, 2, 3])
print(np.exp(x)) # result is (exp(1), exp(2), exp(3))
[ 2.71828183 7.3890561 20.08553692]
Furthermore, if x is a vector, then a Python operation such as s = x + 3 \ s=x+3 s=x+3 or s = 1 x \ s=\frac{1}{x} s=x1 will output s as a vector of the same size as x.
# example of vector operation
x = np.array([1, 2, 3])
print (x + 3)
[4 5 6]
Any time you need more info on a numpy function, we encourage you to look at the official documentation.
You can also create a new cell in the notebook and write np.exp? (for example) to get quick access to the documentation.
Exercise: Implement the sigmoid function using numpy.
Instructions: x could now be either a real number, a vector, or a matrix. The data structures we use in numpy to represent these shapes (vectors, matrices…) are called numpy arrays. You don’t need to know more for now.
F o r x ∈ R n , s i g m o i d ( x ) = s i g m o i d ( x 1 x 2 . . . x n ) = ( 1 1 + e x 1 1 1 + e x 2 . . . 1 1 + e x n ) \ For\quad x\in\mathbb R^n,sigmoid(x)=sigmoid\begin{pmatrix} x_1\\ x_2\\ ...\\ x_n \end{pmatrix}=\begin{pmatrix} \frac{1}{1+e^{x_1}}\\ \frac{1}{1+e^{x_2}}\\ ...\\ \frac{1}{1+e^{x_n}}\\ \end{pmatrix} Forx∈Rn,sigmoid(x)=sigmoid⎝⎜⎜⎛x1x2...xn⎠⎟⎟⎞=⎝⎜⎜⎛1+ex111+ex21...1+exn1⎠⎟⎟⎞
# GRADED FUNCTION: sigmoid
import numpy as np # this means you can access numpy functions by writing np.function() instead of numpy.function()
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1.0 / (1 + 1 / np.exp(x))
### END CODE HERE ###
return s
x = np.array([1, 2, 3])
sigmoid(x)
array([ 0.73105858, 0.88079708, 0.95257413])
1.2 - Sigmoid gradient
Exercise: Implement the function sigmoid_grad() to compute the gradient of the sigmoid function with respect to its input x. The formula is:
s i g m o i d . d e r i v a t i v e s ( x ) = σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \ sigmoid.derivatives(x)=\sigma ^\prime(x)=\sigma(x)(1-\sigma(x)) sigmoid.derivatives(x)=σ′(x)=σ(x)(1−σ(x))
You often code this function in two steps:
1.Set s to be the sigmoid of x. You might find your sigmoid(x) function useful.
2.Compute σ ′ ( x ) = s ( 1 − s ) \ \sigma ^\prime(x)=s(1−s) σ′(x)=s(1−s)
# GRADED FUNCTION: sigmoid_derivative
def sigmoid_derivative(x):
"""
Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
Arguments:
x -- A scalar or numpy array
Return:
ds -- Your computed gradient.
"""
### START CODE HERE ### (≈ 2 lines of code)
s = 1.0 / (1 + 1 / np.exp(x))
ds = s * (1 - s)
### END CODE HERE ###
return ds
x = np.array([1, 2, 3])
print ("sigmoid_derivative(x) = " + str(sigmoid_derivative(x)))
sigmoid_derivative(x) = [ 0.19661193 0.10499359 0.04517666]
1.3 - Reshaping arrays
Two common numpy functions used in deep learning are np.shape and np.reshape().
- X.shape is used to get the shape (dimension) of a matrix/vector X.
- X.reshape(…) is used to reshape X into some other dimension.
For example, in computer science, an image is represented by a 3D array of shape ( l e n g t h , h e i g h t , d e p t h = 3 ) \ (length,height,depth=3) (length,height,depth=3). However, when you read an image as the input of an algorithm you convert it to a vector of shape ( l e n g t h ∗ h e i g h t ∗ 3 , 1 ) \ (length∗height∗3,1) (length∗height∗3,1). In other words, you “unroll”, or reshape, the 3D array into a 1D vector.

Exercise: Implement image2vector() that takes an input of shape (length, height, 3) and returns a vector of shape (lengthheight3, 1). For example, if you would like to reshape an array v of shape (a, b, c) into a vector of shape (a*b,c) you would do:
v = v.reshape((v.shape[0]*v.shape[1], v.shape[2])) # v.shape[0] = a ; v.shape[1] = b ; v.shape[2] = c
- Please don’t hardcode the dimensions of image as a constant. Instead look up the quantities you need with image.shape[0], etc.
# GRADED FUNCTION: image2vector
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
### START CODE HERE ### (≈ 1 line of code)
v = image.reshape((image.shape[0] * image.shape[1] * image.shape[2], 1))
### END CODE HERE ###
return v
# This is a 3 by 3 by 2 array, typically images will be (num_px_x, num_px_y,3) where 3 represents the RGB values
image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print ("image2vector(image) = " + str(image2vector(image)))
image2vector(image) = [[ 0.67826139]
[ 0.29380381]
[ 0.90714982]
[ 0.52835647]
[ 0.4215251 ]
[ 0.45017551]
[ 0.92814219]
[ 0.96677647]
[ 0.85304703]
[ 0.52351845]
[ 0.19981397]
[ 0.27417313]
[ 0.60659855]
[ 0.00533165]
[ 0.10820313]
[ 0.49978937]
[ 0.34144279]
[ 0.94630077]]
1.4 - Normalizing rows
Another common technique we use in Machine Learning and Deep Learning is to normalize our data. It often leads to a better performance because gradient descent converges faster after normalization. Here, by normalization we mean changing x to x ∥ x ∥ \ \frac{x}{∥x∥} ∥x∥x (dividing each row vector of x by its norm).
For example,if
x = [ 0 3 4 2 6 4 ] \ x=\begin{bmatrix} 0 & 3 & 4\\ 2 & 6 & 4\end{bmatrix} x=[023644]
then ∥ x ∥ = n p . l i n a l g . n o r m ( x , a x i s = 1 , k e e p d i m s = T r u e ) = [ 5 56 ] \ \left \| x \right \|=np.linalg.norm(x,axis=1,keepdims=True)=\begin{bmatrix}5\\ \sqrt{56}\end{bmatrix} ∥x∥=np.linalg.norm(x,axis=1,keepdims=True)=[556]
and x . n o r m a l i z e d = x ∥ x ∥ = [ 0 3 5 4 5 2 56 6 56 4 56 ] \ x.normalized=\frac{x}{\left \| x \right\|}=\begin{bmatrix}0&\frac{3}{5} &\frac{4}{5}\\ \frac{2}{\sqrt{56}} &\frac{6}{\sqrt{56}} & \frac{4}{\sqrt{56}} \end{bmatrix} x.normalized=∥x∥x=[05625356654564]
Note that you can divide matrices of different sizes and it works fine: this is called broadcasting and you’re going to learn about it in part 5.
Exercise: Implement normalizeRows() to normalize the rows of a matrix. After applying this function to an input matrix x, each row of x should be a vector of unit length (meaning length 1).
# GRADED FUNCTION: normalizeRows
def normalizeRows(x):
"""
Implement a function that normalizes each row of the matrix x (to have unit length).
Argument:
x -- A numpy matrix of shape (n, m)
Returns:
x -- The normalized (by row) numpy matrix. You are allowed to modify x.
"""
### START CODE HERE ### (≈ 2 lines of code)
# Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, axis = ..., keepdims = True)
x_norm = np.linalg.norm(x, axis=1, keepdims = True) #计算每一行的长度,得到一个列向量
# Divide x by its norm.
x = x / x_norm #利用numpy的广播,用矩阵与列向量相除。
### END CODE HERE ###
return x
x = np.array([
[0, 3, 4],
[1, 6, 4]])
print("normalizeRows(x) = " + str(normalizeRows(x)))
normalizeRows(x) = [[ 0. 0.6 0.8 ]
[ 0.13736056 0.82416338 0.54944226]]
Note:
In normalizeRows(), you can try to print the shapes of x_norm and x, and then rerun the assessment. You’ll find out that they have different shapes. This is normal given that x_norm takes the norm of each row of x. So x_norm has the same number of rows but only 1 column. So how did it work when you divided x by x_norm? This is called broadcasting and we’ll talk about it now!
1.5 - Broadcasting and the softmax function
A very important concept to understand in numpy is “broadcasting”. It is very useful for performing mathematical operations between arrays of different shapes. For the full details on broadcasting, you can read the official broadcasting documentation.
Exercise: Implement a softmax function using numpy. You can think of softmax as a normalizing function used when your algorithm needs to classify two or more classes. You will learn more about softmax in the second course of this specialization.
Instructions:
- f o r x ∈ R 1 × n , s o f t m a x ( x ) = s o f t m a x ( [ x 1 x 2 . . . x n ] ) = [ e x 1 ∑ j e x j e x 2 ∑ j e x j . . . e x n ∑ j e x j ] \ for\quad x\in\mathbb R^{1\times n},softmax(x)=softmax([x_1 \quad x_2 \quad ... \quad x_n])=[\frac{e^{x_1}}{\sum_{j} e^{x_j}} \quad \frac{e^{x_2}}{\sum_{j} e^{x_j}} \quad ... \quad \frac{e^{x_n}}{\sum_{j} e^{x_j}}] forx∈R1×n,softmax(x)=softmax([x1x2...xn])=[∑jexjex1∑jexjex2...∑jexjexn]
- for a matrix x ∈ R m × n \ x\in\mathbb R^{m\times n} x∈Rm×n, x i j \ x_{ij} xij maps to the element in the i t h \ i^{th} ith row and j t h \ j^{th} jth column j t h \ j^{th} jth column of x, thus we have:
s o f t m a x ( x ) = s o f t m a x [ x 11 x 12 x 13 . . . x 1 n x 21 x 22 x 23 . . . x 2 n ⋮ ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 x m 3 . . . x m n ] \ softmax(x)=softmax\begin{bmatrix}x_{11} & x_{12} & x_{13} & ... & x_{1n}\\ x_{21} & x_{22} & x_{23} & ... & x_{2n}\\ \vdots &\vdots & \vdots & \ddots &\vdots \\ x_{m1} & x_{m2} & x_{m3} & ... & x_{mn} \end{bmatrix} softmax(x)=softmax⎣⎢⎢⎢⎡x11x21⋮xm1x12x22⋮xm2x13x23⋮xm3......⋱...x1nx2n⋮xmn⎦⎥⎥⎥⎤
= [ e x 11 ∑ j e x 1 j e x 12 ∑ j e x 1 j e x 13 ∑ j e x 1 j … e x 1 n ∑ j e x 1 j e x 21 ∑ j e x 2 j e x 22 ∑ j e x 2 j e x 23 ∑ j e x 2 j … e x 2 n ∑ j e x 2 j ⋮ ⋮ ⋮ ⋱ ⋮ e x m 1 ∑ j e x m j e x m 2 ∑ j e x m j e x m 3 ∑ j e x m j … e x m n ∑ j e x m j ] \ =\begin{bmatrix}\frac{e^{x_{11}}}{\sum_{j} e^{x_{1j}}} & \frac{e^{x_{12}}} {\sum_{j} e^{x_{1j}}} & \frac{e^{x_{13}}}{\sum_{j} e^{x_{1j}}} & \dots & \frac{e^{x_{1n}}}{\sum_{j} e^{x_{1j}}}\\ \frac{e^{x_{21}}}{\sum_{j} e^{x_{2j}}} & \frac{e^{x_{22}}} {\sum_{j} e^{x_{2j}}} & \frac{e^{x_{23}}}{\sum_{j} e^{x_{2j}}} & \dots & \frac{e^{x_{2n}}}{\sum_{j} e^{x_{2j}}}\\ \vdots &\vdots & \vdots & \ddots &\vdots \\ \frac{e^{x_{m1}}}{\sum_{j} e^{x_{mj}}} & \frac{e^{x_{m2}}} {\sum_{j} e^{x_{mj}}} & \frac{e^{x_{m3}}}{\sum_{j} e^{x_{mj}}} & \dots & \frac{e^{x_{mn}}}{\sum_{j} e^{x_{mj}}}\\ \end{bmatrix} =⎣⎢⎢⎢⎢⎢⎡∑jex1jex11∑jex2jex21⋮∑jexmjexm1∑jex1jex12∑jex2jex22⋮∑jexmjexm2∑jex1jex13∑jex2jex23⋮∑jexmjexm3……⋱…∑jex1jex1n∑jex2jex2n⋮∑jexmjexmn⎦⎥⎥⎥⎥⎥⎤
= ( s o f t m a x ( f i r s t r o w o f x ) s o f t m a x ( s e c o n d r o w o f x ) … s o f t m a x ( l a s t r o w o f x ) ) \ =\begin{pmatrix}softmax(first \quad row \quad of \quad x)\\ softmax(second \quad row \quad of \quad x)\\ \dots\\ softmax(last \quad row \quad of \quad x) \end{pmatrix} =⎝⎜⎜⎛softmax(firstrowofx)softmax(secondrowofx)…softmax(lastrowofx)⎠⎟⎟⎞
# GRADED FUNCTION: softmax
def softmax(x):
"""Calculates the softmax for each row of the input x.
Your code should work for a row vector and also for matrices of shape (n, m).
Argument:
x -- A numpy matrix of shape (n,m)
Returns:
s -- A numpy matrix equal to the softmax of x, of shape (n,m)
"""
### START CODE HERE ### (≈ 3 lines of code)
# Apply exp() element-wise to x. Use np.exp(...).
x_exp = np.exp(x) # (n,m)
# Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
x_sum = np.sum(x_exp, axis = 1, keepdims = True) # (n,1)
# Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
s = x_exp / x_sum # (n,m) 广播的作用
### END CODE HERE ###
return s
x = np.array([
[9, 2, 5, 0, 0],
[7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(x)))
softmax(x) = [[ 9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
1.21052389e-04]
[ 8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
8.01252314e-04]]
Note:
- If you print the shapes of x_exp, x_sum and s above and rerun the assessment cell, you will see that x_sum is of shape (2,1) while x_exp and s are of shape (2,5). x_exp/x_sum works due to python broadcasting.
What you need to remember:
- np.exp(x) works for any np.array x and applies the exponential function to every coordinate
- the sigmoid function and its gradient
- image2vector is commonly used in deep learning
- np.reshape is widely used. In the future, you’ll see that keeping your matrix/vector dimensions straight will go toward eliminating a lot of bugs.
- numpy has efficient built-in functions
- broadcasting is extremely useful
2) Vectorization
In deep learning, you deal with very large datasets. Hence, a non-computationally-optimal function can become a huge bottleneck in your algorithm and can result in a model that takes ages to run. To make sure that your code is computationally efficient, you will use vectorization. For example, try to tell the difference between the following implementations of the dot/outer/elementwise product.
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
tic = time.process_time()
dot = 0
for i in range(len(x1)):
dot+= x1[i]*x2[i]
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
tic = time.process_time()
outer = np.zeros((len(x1),len(x2))) # we create a len(x1)*len(x2) matrix with only zeros
for i in range(len(x1)):
for j in range(len(x2)):
outer[i,j] = x1[i]*x2[j]
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC ELEMENTWISE IMPLEMENTATION ###
tic = time.process_time()
mul = np.zeros(len(x1))
for i in range(len(x1)):
mul[i] = x1[i]*x2[i]
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
tic = time.process_time()
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
for j in range(len(x1)):
gdot[i] += W[i,j]*x1[j]
toc = time.process_time()
print ("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
dot = 278
----- Computation time = 0.2854390000002205ms
outer = [[ 81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0.
0.]
[ 18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0.
0.]
[ 45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 63. 14. 14. 63. 0. 63. 14. 35. 0. 0. 63. 14. 35. 0.
0.]
[ 45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0.
0.]
[ 18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0.
0.]
[ 45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]]
----- Computation time = 0.340502999999881ms
elementwise multiplication = [ 81. 4. 10. 0. 0. 63. 10. 0. 0. 0. 81. 4. 25. 0. 0.]
----- Computation time = 0.21034700000011064ms
gdot = [ 31.19670632 24.24358575 24.08807423]
----- Computation time = 0.4973530000000892ms
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
dot = 278
----- Computation time = 0.17332000000003234ms
outer = [[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[63 14 14 63 0 63 14 35 0 0 63 14 35 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
----- Computation time = 0.15053899999983855ms
elementwise multiplication = [81 4 10 0 0 63 10 0 0 0 81 4 25 0 0]
----- Computation time = 0.11027100000005063ms
gdot = [ 31.19670632 24.24358575 24.08807423]
----- Computation time = 0.22889199999998056ms
As you may have noticed, the vectorized implementation is much cleaner and more efficient. For bigger vectors/matrices, the differences in running time become even bigger.
Note that np.dot() performs a matrix-matrix or matrix-vector multiplication. This is different from np.multiply() and the * operator (which is equivalent to.* in Matlab/Octave), which performs an element-wise multiplication.
2.1 Implement the L1 and L2 loss functions
Exercise: Implement the numpy vectorized version of the L1 loss. You may find the function abs(x) (absolute value of x) useful.
Reminder:
- The loss is used to evaluate the performance of your model. The bigger your loss is, the more different your predictions ( y ^ ) \ (\hat{y}) (y^) are from the true values ( y ) \ (y) (y). In deep learning, you use optimization algorithms like Gradient Descent to train your model and to minimize the cost.
- L1 loss is defined as:
L 1 ( y ^ , y ) = ∑ i = 0 m ∣ y ( i ) − y ^ ( i ) ∣ \ L_1(\hat{y},y)=\sum_{i=0}^m \left| y^{(i)}-\hat{y}^{(i)} \right| L1(y^,y)=i=0∑m∣∣∣y(i)−y^(i)∣∣∣
# GRADED FUNCTION: L1
def L1(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L1 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
loss = np.sum(np.abs(y - yhat))
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
L1 = 1.1
Exercise: Implement the numpy vectorized version of the L2 loss. There are several way of implementing the L2 loss but you may find the function np.dot() useful. As a reminder, if x = [ x 1 , x 2 , . . . , x n ] x = [ x 1 , x 2 , . . . , x n ] \ x=[x_1,x_2,...,x_n]x=[x_1,x_2,...,x_n] x=[x1,x2,...,xn]x=[x1,x2,...,xn], then np.dot(x,x) = ∑ j = 0 n x j 2 \ =\sum_{j=0}^n x^2_j =∑j=0nxj2.
- L2 loss is defined as
L 2 ( y ^ , y ) = ∑ i = 0 m ( y ( i ) − y ^ ( i ) ) 2 \ L_2(\hat{y},y)=\sum_{i=0}^m ( y^{(i)}-\hat{y}^{(i)} )^2 L2(y^,y)=i=0∑m(y(i)−y^(i))2
# GRADED FUNCTION: L2
def L2(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L2 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
loss =np.sum(np.power((y - yhat), 2))
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))
L2 = 0.43
What you need to remember:
- Vectorization is very important in deep learning. It provides computational efficiency and clarity.
- You have reviewed the L1 and L2 loss.
- You are familiar with many numpy functions such as np.sum, np.dot, np.multiply, np.maximum, etc…
Part 2: Logistic Regression with a Neural Network mindset
You will learn to:
- Build the general architecture of a learning algorithm, including:
- Initializing parameters
- Calculating the cost function and its gradient
- Using an optimization algorithm (gradient descent)
- Gather all three functions above into a main model function, in the right order.
1 - Packages
First, let’s run the cell below to import all the packages that you will need during this assignment.
- numpy is the fundamental package for scientific computing with Python.
- h5py is a common package to interact with a dataset that is stored on an H5 file.
- matplotlib is a famous library to plot graphs in Python.
- PIL and scipy are used here to test your model with your own picture at the end.
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
% matplotlib inline
请点这里下载dataset and lr_utils函数下载数据集及相关函数.
PS: 这里导入数据集有很多人都不会,具体操作可以看我另一篇博客,请点。
2 - Overview of the Problem set
Problem Statement: You are given a dataset (“data.h5”) containing:
- a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
- a test set of m_test images labeled as cat or non-cat
- each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
You will build a simple image-recognition algorithm that can correctly classify pictures as cat or non-cat.
Let’s get more familiar with the dataset. Load the data by running the following code.
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
We added “_orig” at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don’t need any preprocessing).
Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the index value and re-run to see other images.
# Example of a picture
index = 50
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
y = [1], it's a 'cat' picture.

Many software bugs in deep learning come from having matrix/vector dimensions that don’t fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
Exercise: Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px (= height = width of a training image)
Remember thattrain_set_x_origis a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can accessm_trainby writingtrain_set_x_orig.shape[0].
### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
Number of training examples: m_train = 209
Number of testing examples: m_test = 50
Height/Width of each image: num_px = 64
Each image is of size: (64, 64, 3)
train_set_x shape: (209, 64, 64, 3)
train_set_y shape: (1, 209)
test_set_x shape: (50, 64, 64, 3)
test_set_y shape: (1, 50)
For convenience, you should now reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px∗num_px∗3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
Exercise: Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num_px∗num_px∗3, 1).
A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b∗c∗d, a) is to use:
X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = train_set_x_orig.reshape(m_train, -1).T
test_set_x_flatten = test_set_x_orig.reshape(m_test, -1).T
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)
sanity check after reshaping: [17 31 56 22 33]
To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
Let’s standardize our dataset.
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
What you need to remember:
Common steps for pre-processing a new dataset are:
- Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, …)
- Reshape the datasets such that each example is now a vector of size (num_px * num_px * 3, 1)
- “Standardize” the data
3 - General Architecture of the learning algorithm
It’s time to design a simple algorithm to distinguish cat images from non-cat images.
You will build a Logistic Regression, using a Neural Network mindset. The following Figure explains why Logistic Regression is actually a very simple Neural Network!
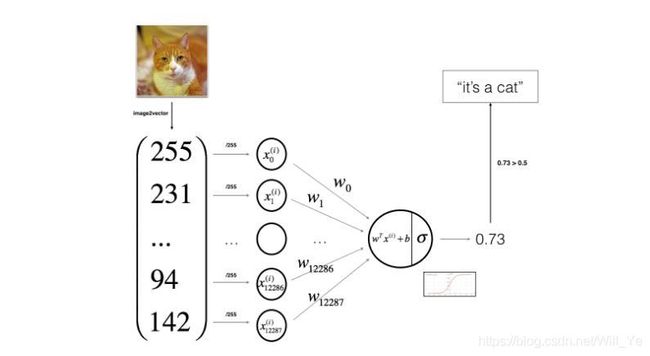
Mathematical expression of the algorithm:
For one example x ( i ) \ x^{(i)} x(i):
z ( i ) = w T x ( i ) + b \ z^{(i)}=w^Tx^{(i)}+b z(i)=wTx(i)+b
y ^ ( i ) = a ( i ) = s i g m o i d ( z ( i ) ) \ \hat{y}^{(i)}=a^{(i)}=sigmoid(z^{(i)}) y^(i)=a(i)=sigmoid(z(i))
L ( a ( i ) , y ( i ) ) = − y ( i ) l o g ( a ( i ) ) − ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) \ L(a^{(i)},y^{(i)})=-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)}) L(a(i),y(i))=−y(i)log(a(i))−(1−y(i))log(1−a(i))
The cost is then computed by summing over all training examples:
J = 1 m ∑ i = 1 m L ( a ( i ) , y ( i ) ) \ J=\frac{1}{m}\sum_{i=1}^m L(a^{(i)},y^{(i)}) J=m1i=1∑mL(a(i),y(i))
Key steps:
In this exercise, you will carry out the following steps:
- Initialize the parameters of the model
- Learn the parameters for the model by minimizing the cost
- Use the learned parameters to make predictions (on the test set)
- Analyse the results and conclude
4 - Building the parts of our algorithm
The main steps for building a Neural Network are:
- Define the model structure (such as number of input features)
- Initialize the model’s parameters
- Loop:
- Calculate current loss (forward propagation)
- Calculate current gradient (backward propagation)
- Update parameters (gradient descent)
You often build 1-3 separately and integrate them into one function we call model().
4.1 - Helper functions
Exercise: Using your code from “Python Basics”, implement sigmoid(). As you’ve seen in the figure above, you need to compute s i g m o i d ( w T x + b ) = 1 1 + e − ( w T x + b ) \ sigmoid(w^Tx+b)=\frac{1}{1+e^{−(w^Tx+b)}} sigmoid(wTx+b)=1+e−(wTx+b)1 to make predictions. Use np.exp().
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1/(1+np.exp(-z))
### END CODE HERE ###
return s
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
sigmoid([0, 2]) = [ 0.5 0.88079708]
4.2 - Initializing parameters
Exercise: Implement parameter initialization in the cell below. You have to initialize w as a vector of zeros. If you don’t know what numpy function to use, look up np.zeros() in the Numpy library’s documentation.
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros((dim, 1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
w = [[ 0.]
[ 0.]]
b = 0
For image inputs, w will be of shape (num_px x num_px × 3, 1).
4.3 - Forward and Backward propagation
Now that your parameters are initialized, you can do the “forward” and “backward” propagation steps for learning the parameters.
Exercise: Implement a function propagate() that computes the cost function and its gradient.
Hints:
Forward Propagation:
- You get X
- You compute A = σ ( w T X + b ) = ( a ( 0 ) , a ( 1 ) , … , a ( m − 1 ) , a ( m ) ) \ A=\sigma(w^TX+b)=(a^{(0)},a^{(1)},\dots,a^{(m−1)},a^{(m)}) A=σ(wTX+b)=(a(0),a(1),…,a(m−1),a(m))
- You calculate the cost function: J = − 1 m ∑ i = 1 m y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) \ J=−\frac{1}{m}\sum_{i=1}^m y^{(i)}log(a^{(i)})+(1−y^{(i)})log(1−a^{(i)}) J=−m1∑i=1my(i)log(a(i))+(1−y(i))log(1−a(i))
Here are the two formulas you will be using:
d J d w = 1 m X ( A − Y ) T \ \frac{dJ}{dw}=\frac{1}{m}X(A-Y)^T dwdJ=m1X(A−Y)T
d J d b = 1 m ∑ i = 1 m ( a ( i ) − y ( i ) ) \ \frac{dJ}{db}=\frac{1}{m}\sum_{i=1}^m (a^{(i)}−y^{(i)}) dbdJ=m1i=1∑m(a(i)−y(i))
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = sigmoid(np.dot(w.T, X)+b) # compute activation
cost = -(1.0/m)*np.sum(Y*np.log(A)+(1-Y)*np.log(1-A)) # compute cost
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = (1.0/m)*np.dot(X,(A-Y).T)
db = (1.0/m)*np.sum(A-Y)
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
dw = [[ 0.99845601]
[ 2.39507239]]
db = 0.00145557813678
cost = 5.80154531939
d) Optimization
- You have initialized your parameters.
- You are also able to compute a cost function and its gradient.
- Now, you want to update the parameters using gradient descent.
Exercise: Write down the optimization function. The goal is to learn w \ w w and b \ b b by minimizing the cost function J \ J J. For a parameter θ \ θ θ, the update rule is θ = θ − α d θ \ θ=θ−α dθ θ=θ−αdθ, where α \ α α is the learning rate.
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = w - learning_rate*dw
b = b - learning_rate*db
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
w = [[-0.08608643]
[ 0.10971233]]
b = -0.1442742664803268
dw = [[0.12311093]
[0.13629247]]
db = -0.14923915884638042
Exercise: The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the predict() function. There is two steps to computing predictions:
- Calculate Y ^ = A = σ ( w T X + b ) \ \hat{Y}=A=\sigma(w^TX+b) Y^=A=σ(wTX+b)
- Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5), stores the predictions in a vector
Y_prediction. If you wish, you can use anif/elsestatement in aforloop (though there is also a way to vectorize this).
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1) #X.shape[0]代表特征数个数,w是权重
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(w.T, X) + b)
### END CODE HERE ###
for i in range(A.shape[1]): #A.shape[1]=列数即输入样本数
# Convert probabilities A[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
if A[0,i] > 0.5:
Y_prediction[0,i] = 1
else:
Y_prediction[0,i] = 0
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]]) # X.shape[1]=3
print ("predictions = " + str(predict(w, b, X)))
predictions = [[ 1. 1. 0.]]
What you need to remember:
You’ve implemented several functions that:
- Initialize (w,b)
- Optimize the loss iteratively to learn parameters (w,b):
- computing the cost and its gradient
- updating the parameters using gradient descent
- Use the learned (w,b) to predict the labels for a given set of examples
5 - Merge all functions into a model
You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
Exercise: Implement the model function. Use the following notation:
- Y_prediction for your predictions on the test set
- Y_prediction_train for your predictions on the train set
- w, costs, grads for the outputs of optimize()
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (≈ 1 line of code)
w, b = initialize_with_zeros(X_train.shape[0])
# Gradient descent (≈ 1 line of code)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test, #(1*50)
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
Run the following cell to train your model.
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
train accuracy: 99.04306220095694 %
test accuracy: 70.0 %
Comment: Training accuracy is close to 100%. This is a good sanity check: your model is working and has high enough capacity to fit the training data. Test error is 68%. It is actually not bad for this simple model, given the small dataset we used and that logistic regression is a linear classifier. But no worries, you’ll build an even better classifier next week!
Also, you see that the model is clearly overfitting the training data. Later in this specialization you will learn how to reduce overfitting, for example by using regularization. Using the code below (and changing the index variable) you can look at predictions on pictures of the test set.
# Example of a picture that was wrongly classified.
index = 10
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
#下面classes中括号内一定要加int限定预测值为整数,不然会有小数点,导致无法显示
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a '"+ classes[int(d["Y_prediction_test"][0,index])].decode("utf-8") + "' picture.")
y = 1, you predicted that it is a 'non-cat' picture. #可见,准确率不是特别的高,明明是一张白猫的图片,没检测出来
Let’s also plot the cost function and the gradients.
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

Interpretation:
You can see the cost decreasing. It shows that the parameters are being learned. However, you see that you could train the model even more on the training set. Try to increase the number of iterations in the cell above and rerun the cells. You might see that the training set accuracy goes up, but the test set accuracy goes down. This is called overfitting.
6 - Further analysis (optional/ungraded exercise)
Congratulations on building your first image classification model. Let’s analyze it further, and examine possible choices for the learning rate α \ α α.
Choice of learning rate
Reminder:
In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate αα determines how rapidly we update the parameters. If the learning rate is too large we may “overshoot” the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That’s why it is crucial to use a well-tuned learning rate.
Let’s compare the learning curve of our model with several choices of learning rates. Run the cell below. This should take about 1 minute. Feel free also to try different values than the three we have initialized the learning_rates variable to contain, and see what happens.
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
learning rate is: 0.01
train accuracy: 99.52153110047847 %
test accuracy: 68.0 %
-------------------------------------------------------
learning rate is: 0.001
train accuracy: 88.99521531100478 %
test accuracy: 64.0 %
-------------------------------------------------------
learning rate is: 0.0001
train accuracy: 68.42105263157895 %
test accuracy: 36.0 %
-------------------------------------------------------
- Different learning rates give different costs and thus different predictions results.
- If the learning rate is too large (0.01), the cost may oscillate up and down. It may even diverge (though in this example, using 0.01 still eventually ends up at a good value for the cost).
- A lower cost doesn’t mean a better model. You have to check if there is possibly overfitting. It happens when the training accuracy is a lot higher than the test accuracy.
- In deep learning, we usually recommend that you:
- Choose the learning rate that better minimizes the cost function.
- If your model overfits, use other techniques to reduce overfitting. (We’ll talk about this in later videos.)
7 - Test with your own image (optional/ungraded exercise)
Congratulations on finishing this assignment. You can use your own image and see the output of your model. To do that:
- Click on “File” in the upper bar of this notebook, then click “Open” to go on your Coursera Hub.
- Add your image to this Jupyter Notebook’s directory, in the “images” folder
- Change your image’s name in the following code
- Run the code and check if the algorithm is right (1 = cat, 0 = non-cat)!
## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "cat06.jpeg" # 图片名根据自己的图片命名来修改,注意要jpeg格式,用jpg格式不知道为什么不行,检测的结构全是non-cat
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image #测试图片所在的路径,根据实际情况调整
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((1, num_px*num_px*3)).T
my_predicted_image = predict(d["w"], d["b"], my_image)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
y = 1.0, your algorithm predicts a "cat" picture.
What to remember from this assignment:
1. Preprocessing the dataset is important.
2. You implemented each function separately: initialize(), propagate(), optimize(). Then you built a model().
3. Tuning the learning rate (which is an example of a “hyperparameter”) can make a big difference to the algorithm. You will see more examples of this later in this course!

