【机器学习】K-means算法Python实现教程
本文内容
阅读须知:
- 阅读本文需要有一定的Python及Numpy基础
本文将介绍:
- K-means算法实现步骤
- 使用Python实现K-means算法
- 借助Numpy的向量计算提升计算速度
- 使用Gap Statistic法自动选取合适的聚类中心数K
K-means简介
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。
k均值聚类是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中。
K-means原理
设有样本 ( x 1 , x 2 , . . . , x n ) (x_1, x_2, ..., x_n) (x1,x2,...,xn),其中每个样本有d个特征(由d维实向量组成),K-means聚类的目标是将 n n n个样本聚类至 k ( ≤ n ) k(\le n) k(≤n)个集合 S = { S 1 , S 2 , . . . , S k } S = \{S_1, S_2, ..., S_k\} S={S1,S2,...,Sk} 中,使簇中样本的距离和达到最小。
即用公式表示为:
arg min S ∑ i = 1 k ∑ x ∈ S i ∥ x − μ i ∥ 2 = arg min S ∑ i = 1 k ∣ S i ∣ Var S i {\displaystyle {\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}={\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}|S_{i}|\operatorname {Var} S_{i}} Sargmini=1∑kx∈Si∑∥x−μi∥2=Sargmini=1∑k∣Si∣VarSi
其中 μ i \mu _i μi 是 S i S_i Si中所有点的质心,因此上式相当于最小化簇中每两点的平方距离:
arg min S ∑ i = 1 k 1 ∣ S i ∣ ∑ x , y ∈ S i ∥ x − y ∥ 2 {\displaystyle {\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\,{\frac {1}{|S_{i}|}}\,\sum _{\mathbf {x} ,\mathbf {y} \in S_{i}}\left\|\mathbf {x} -\mathbf {y} \right\|^{2}} Sargmini=1∑k∣Si∣1x,y∈Si∑∥x−y∥2
K-means步骤
K-means算法根据此从距离入手,迭代找出(局部)最小时的聚类中心 S i S_i Si。具体步骤如下:
- 选择初始化的 k k k 个样本作为初始聚类中心 a = { a 1 , a 2 , . . . , a k } a = \{a_1, a_2, ..., a_k\} a={a1,a2,...,ak};
- 针对数据集中每个样本 x i x_i xi计算它到 k k k 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中;
- 针对每个类别 S j S_j Sj,重新计算它的聚类中心 a j = 1 ∣ S i ∣ ∑ x ∈ S i x a_j=\frac{1}{\left | S_i \right | } {\textstyle \sum_{x\in S_i}x} aj=∣Si∣1∑x∈Six;
- 重复上面2、3两步操作,直到达到某个中止条件(迭代次数、最小误差变化等)。
Python实现
基本实现
- 需要用聚类中心数量k进行初始化,此外可以给定迭代次数与最小误差等终止条件。
- fit函数以若干n维特征的数据作为输入。执行后,通过classifications获取分类结果;centroids获取聚类中心。
- Predict函数以一个n维特征的数据作为输入,输出归属的聚类中心索引。
- 每步操作的作用详见代码注释
class Kmeans:
def __init__(self, k=2, tolerance=0.01, max_iter=300):
self.k = k
self.tol = tolerance
self.max_iter = max_iter
self.features_count = -1
self.classifications = None
self.centroids = None
def fit(self, data):
"""
:param data: numpy数组,约定shape为:(数据数量,数据维度)
:type data: numpy.ndarray
"""
self.features_count = data.shape[1]
# 初始化聚类中心(维度:k个 * features种数)
self.centroids = np.zeros([self.k, data.shape[1]])
for i in range(self.k):
self.centroids[i] = data[i]
for i in range(self.max_iter):
# 清空聚类列表
self.classifications = [[] for i in range(self.k)]
# 对每个点与聚类中心进行距离计算
for feature_set in data:
# 预测分类
classification = self.predict(feature_set)
# 加入类别
self.classifications[classification].append(feature_set)
# 记录前一次的结果
prev_centroids = np.ndarray.copy(self.centroids)
# 更新中心
for classification in range(self.k):
self.centroids[classification] = np.average(self.classifications[classification], axis=0)
# 检测相邻两次中心的变化情况
for c in range(self.k):
if np.linalg.norm(prev_centroids[c] - self.centroids[c]) > self.tol:
break
# 如果都满足条件(上面循环没break),则返回
else:
return
def predict(self, data):
# 距离
distances = np.linalg.norm(data - self.centroids, axis=1)
# 最小距离索引
return distances.argmin()
测试代码
blobs函数产生若干个数据点云。n_features是维度,centers是中心数目,random_state是随机种子。
from sklearn.datasets import make_blobs
def blobs(n_samples=300, n_features=2, centers=1, cluster_std=0.60, random_state=0):
points, _ = make_blobs(n_samples=n_samples,
n_features=n_features,
centers=centers,
cluster_std=cluster_std,
random_state=random_state)
return points
输出聚类图象的函数,支持2D和3D,8类别以内不同颜色区分。
def kmeans_plot(kmeans_model):
"""
又长又臭的函数,简单可视化2d或3d kmeans聚类结果,不是算法必须的,直接使用即可。
:param kmeans_model: 训练的kmeans模型
:type kmeans_model: Kmeans | FastKmeans
"""
style.use('ggplot')
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'w']
# 2D
if kmeans_model.features_count == 2:
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot()
for i in range(kmeans_model.k):
color = colors[i%len(colors)]
for feature_set in kmeans_model.classifications[i]:
ax.scatter(feature_set[0], feature_set[1], marker="x", color=color, s=50, linewidths=1)
for centroid in kmeans_model.centroids:
ax.scatter(centroid[0], centroid[1], marker="o", color="k", s=50, linewidths=3)
# 3D
elif kmeans_model.features_count == 3:
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(projection='3d')
for i in range(kmeans_model.k):
color = colors[i%len(colors)]
for feature_set in kmeans_model.classifications[i]:
ax.scatter(feature_set[0], feature_set[1], feature_set[2], marker="x", color=color, s=50, linewidths=1)
for centroid in kmeans_model.centroids:
ax .scatter(centroid[0], centroid[1], centroid[2], marker="o", color="k", s=50, linewidths=3)
plt.show()
测试调用
model = Kmeans(k=3)
model.fit(blobs(centers=3, random_state=1, n_features=2))
kmeans_plot(model)
model.fit(blobs(centers=3, random_state=3, n_features=3))
kmeans_plot(model)
测试结果
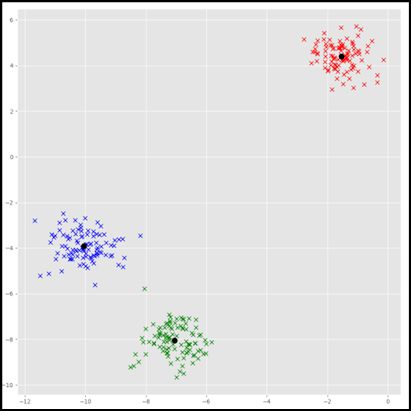
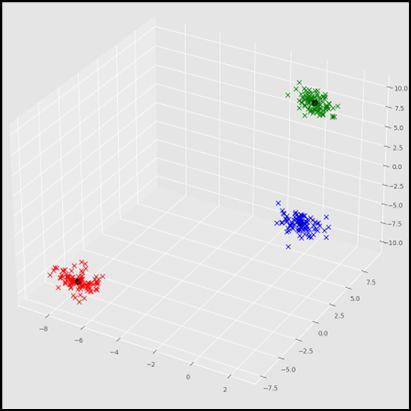
计算效率问题
问题描述
该实现虽然可以使用,但是在进行大规模数据处理时非常慢,通过性能监控找出耗时最大的过程:
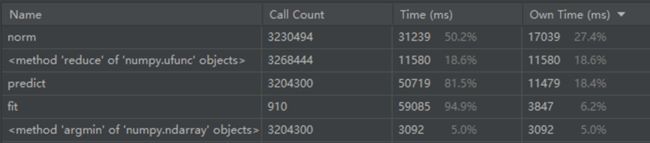
问题分析
分析后发现:距离计算的函数被调用了很多次。进而说明,主要函数(如距离)的计算单位是小规模点集,因此这些函数在python层面上调用了多次。众所周知python的执行效率比较慢,特别是耗时排第一的norm函数,对于小规模计算的开销是极大的。
解决办法
最好的解决办法是计算向量化:设法一次计算一批、甚至全部数据。这样就可以把计算交给python底层的c语言实现;而且向量(或矩阵)的计算本身也是被优化过的。如此速度上会提升许多。
计算优化实现
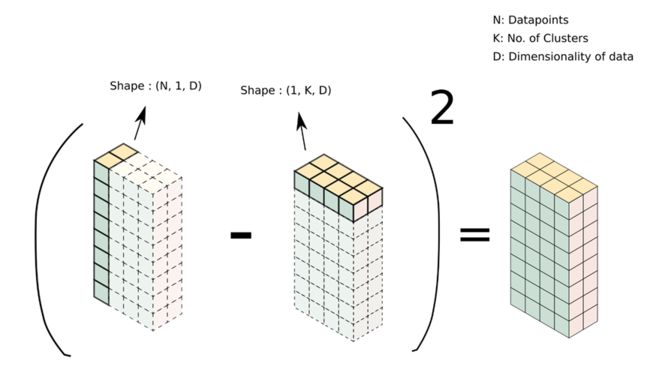
numpy广播
计算优化借助了numpy库中向量广播的特性。
如下图,被减数是(N, 1, D)维向量,表示N个D维数据的数据集;减数是(1, K, D)维向量,表示K个D维的聚类中心。相减时,由于向量维度不匹配,numpy会将向量广播为矩阵(结果为虚线表示的矩阵)再相减。而该例子中,所得结果矩阵恰好为:每个点与各个聚类中心的距离信息。
实现代码
- compute_l2_distance利用了numpy广播
class FastKmeans:
def __init__(self, k=2, tolerance=0.01, max_iter=300):
self.k = k
self.tol = tolerance
self.max_iter = max_iter
self.features_count = -1
self.classifications = None
self.centroids = None
def fit(self, data):
"""
:param data: numpy数组,约定shape为:(数据数量,数据维度)
:type data: numpy.ndarray
"""
self.features_count = data.shape[1]
# 初始化聚类中心(维度:k个 * features种数)
self.centroids = np.zeros([self.k, data.shape[1]])
for i in range(self.k):
self.centroids[i] = data[i]
points_centroid = np.zeros(data.shape[0])
for i in range(self.max_iter):
prev_centroid = np.ndarray.copy(points_centroid)
points_centroid = self.get_closest_centroid(data)
for c in range(self.centroids.shape[0]):
# 获取该类的点
classification = data[points_centroid == c]
# 更新聚类中心
self.centroids[c] = classification.mean(axis=0)
if FastKmeans.compute_l2_distance(prev_centroid, points_centroid) < self.tol:
break
self.classifications = []
for c in range(self.centroids.shape[0]):
# 获取该类的点
self.classifications.append(data[points_centroid == c])
def predict(self, data):
# 距离
distances = np.linalg.norm(data - self.centroids, axis=1)
# 最小距离索引
return distances.argmin()
@staticmethod
def compute_l2_distance(x, centroid):
# 利用numpy广播计算
dist = ((x - centroid) ** 2).sum(axis=x.ndim - 1)
return dist
def get_closest_centroid(self, x):
# 遍历每个中心,并计算中心与该点间的距离
dist = FastKmeans.compute_l2_distance(x[:, None, :], self.centroids[None, :, :])
# 取得距离最小的中心的索引
closest_centroid_index = np.argmin(dist, axis=1)
return closest_centroid_index
速度对比
每组对比实验分别使用两种做法对n个数据进行从1到20类的聚类。记录两种做法分别的耗时。
| 500 | 1000 | 5000 | 10000 | 20000 | |
|---|---|---|---|---|---|
| 普通实现 | 0.86 | 2.91 | 23.72 | 59.17 | 129.69 |
| 计算优化实现 | 0.07 | 0.98 | 3.84 | 6.41 | 28.34 |
| 比率 | 12.2857 | 2.9694 | 6.1771 | 9.2309 | 4.5762 |
可见在不同的数据规模下均有一定提升。两种做法的速度差距在之后选择k的过程中更加明显。
自动K值选取
常用方法
手肘法
其思想是:
随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。
当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大;而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。
但该做法的缺点是需要人工判断“手肘”位置到底在哪,在类别多时难以判断。
Gap statistic
其定义为:
G a p ( K ) = E ( l o g D k ) − l o g D k Gap(K)=E(logD_k)-logD_k Gap(K)=E(logDk)−logDk
其中, E ( l o g D k ) E(logD_k) E(logDk)是 l o g D k logD_k logDk的期望,一般使用蒙特卡洛模拟产生。
简单解释
模拟的基本过程是:首先在样本所在区域内按照均匀分布随机地产生和原始样本数一样多的随机样本,并用K-means模型对这个随机样本聚类,计算结果的误差和,得到一个 D k D_k Dk。重复多次就可以近似计算出 E ( l o g D k ) E(logD_k) E(logDk)。
实际上,计算 E ( l o g D k ) E(logD_k) E(logDk)只是为了给评判实际误差 l o g D k logD_k logDk提供一个标准。当选取合适的 K K K值时, D k D_k Dk应处于偏离(远低于)平均值的极端情况,因此通过与期望误差做差,得到最大 G a p ( K ) Gap(K) Gap(K)所对应的K即是最好的选择。
详细解释
- 原理性较强,非必须理解
- 本节内容翻译自原论文
设聚类簇 C r C_r Cr中两点间距离和为:
D r = ∑ i , i ′ ∈ C r d i i ′ D_r=\sum_{i,i'\in C_r} d_{ii'} Dr=i,i′∈Cr∑dii′
若 d i i ′ d_{ii'} dii′为欧几里得距离,则可定义“每个簇内平方和均值”的总加和 W k W_k Wk为:
W k = ∑ r = 1 k 1 2 n r D r W_k=\sum_{r=1}^{k}\frac{1}{2n_r}D_r Wk=r=1∑k2nr1Dr
其中因子 2 2 2恰好使上式成立;数据规模 n n n被约分掉了。
该方法通过与一个合适的零分布比较来标准化 log ( W k ) \log(W_k) log(Wk),而最优聚类数则是使 log ( W k ) \log(W_k) log(Wk)最偏离于上述参考分布时的值 k k k。因此定义:
G a p n ( k ) = E n ∗ { log ( W k ) } − log ( W k ) Gap_n(k)=E_n^*\{\log(W_k)\}-\log(W_k) Gapn(k)=En∗{log(Wk)}−log(Wk)
其中 E n ∗ E_n^* En∗表示样本规模 n n n的数据在参考分布中的数学期望。考虑抽样分布后,使 G a p n ( k ) Gap_n(k) Gapn(k)最大化的值就是所估计聚类数 k k k的最优值。
这个方法的操作是一般化的,可以用在以任意形式计算距离 d i i ′ d_{ii'} dii′的任意的聚类方法。
Gap Statistic的思路启发是:假设有n个、k簇、均匀分布的p维数据点,设想它们在各自的簇中均匀分布,则 log ( W k ) \log(W_k) log(Wk)的期望近似是:
log ( p n 12 ) − ( 2 p ) log ( k ) + C o n s t a n t \log(\frac{pn}{12})-(\frac{2}{p})\log(k)+Constant log(12pn)−(p2)log(k)+Constant
如果数据确实有K个相互分离的聚类,对于 k ≤ K k\le K k≤K, log ( W k ) \log(W_k) log(Wk)应比预期下降率 ( 2 p ) log ( k ) (\frac{2}{p})\log(k) (p2)log(k)下降的更快;当 k > K k \gt K k>K,事实上是在加入不必要的聚类中心,此时由简单代数可得 log ( W k ) \log(W_k) log(Wk)应下降的比其预期速率更慢。因此 G a p n ( K ) Gap_n(K) Gapn(K)会在 k = K k=K k=K时取得最大值。
使用Gap Statistic选取最优的k
首先,该算法需要评估聚类误差 D k D_k Dk,由于最后的标准是相对的,因此 D k D_k Dk的求法并无过多约束,只要能体现其误差即可,因此还是选择最简便的做法:各点到聚类中心的距离为单个误差,将其加和作为最终的误差,由sum_distance处理这一过程。
虽然聚类中心K的最优解是不依赖算法客观存在的,但由于不同K-means实现会得出不同的 D k D_k Dk,因此为了 G a p ( K ) Gap(K) Gap(K)具有可比性,需要借助同一种K-means实现求解误差 D k D_k Dk,因此sum_distance中统一使用FastKmeans。
import scipy
def sum_distance(data, k):
model = FastKmeans(k=k)
model.fit(data)
disp = 0
for m in range(len(model.classifications)):
disp += sum(np.linalg.norm(model.classifications[m] - model.centroids[m], axis=1))
return disp
gap函数需要给定k的测试范围ks以及蒙特卡洛模拟次数nrefs,负责产生随机样品估计 E ( l o g D k ) E(logD_k) E(logDk)、计算 l o g D k logD_k logDk,然后返回范围内各个 k k k值对应的 G a p ( K ) Gap(K) Gap(K)值。
def gap(data, refs=None, nrefs=20, ks=range(1, 11)):
shape = data.shape
if refs == None:
tops = data.max(axis=0)
bots = data.min(axis=0)
dists = scipy.matrix(np.diag(tops - bots))
rands = scipy.random.random_sample(size=(shape[0], shape[1], nrefs))
for i in range(nrefs):
rands[:, :, i] = rands[:, :, i] * dists + bots
else:
rands = refs
gaps = np.zeros((len(ks),))
for (i, k) in enumerate(ks):
disp = sum_distance(data, k)
refdisps = np.zeros((rands.shape[2],))
for j in range(rands.shape[2]):
refdisps[j] = sum_distance(rands[:, :, j], k)
gaps[i] = np.lib.scimath.log(np.mean(refdisps)) - np.lib.scimath.log(disp)
return gaps
调用代码
先生成随机点云,此处生成了一组6个聚类中心的3维点云。
之后调用gap函数。
my_data = blobs(centers=6, random_state=121, n_features=3)
gaps = gap(my_data, nrefs=100)
结果输出
此处顺便做了之前两种实现的效率对比,下面两个输出分别对应K-means和Fast K-means实现。
[-0.05127935 -0.01656365 0.30313623 0.78059812 1.56439394 1.70980351
1.67235943 1.63859173 1.62538263 -0.84390957]
best k: 6
58.349995613098145
[-0.05141505 -0.01660111 0.30252902 0.78299894 1.56696863 1.70689603
1.67327937 1.63563849 1.62526949 -0.8487873 ]
best k: 6
4.088269472122192
结果分析
可以看到两种实现的gap值(两个列表输出)有略微不同,但都得到 k = 6 k=6 k=6的结果,而之前生成的数据正是 6 6 6个中心,说明算法成功检测出最优的 k k k值。
此外,可以看到K-means版本的gap函数运行需要58秒,而Fast K-means只需要4秒,速度差距超过十倍,之前的优化还算是效果拔群的。
Gap Statistic总结
- 理论上可以自动化找出最优的K。
- 但由于实现上需要借助特定的K-means算法,而K-means具有局部最优的特点,因此该算法找出的K并不一定是最优的。
- 再加上期望使用蒙特卡洛方法,想得到稳定、靠谱的答案需要花费更多时间进行频率测试。
- 有时会出现多个峰值(设想3类别聚类完全可以对半分成6类),一般根据经验主义选取第一个。
- 无论如何,用于自动化估计较优的K,Gap statistic已经足够了。
参考文献
[1] Tibshirani R , Hastie W T . Estimating the number of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society B, 2001, 63(2):411-423.
非文献参考
【机器学习】K-means(非常详细)
https://zhuanlan.zhihu.com/p/78798251
A Python implementation of the Gap Statistic
https://gist.github.com/michiexile/5635273
Nuts and Bolts of NumPy Optimization Part 2: Speed Up K-Means Clustering by 70x
https://blog.paperspace.com/speed-up-kmeans-numpy-vectorization-broadcasting-profiling/