泰坦尼克号生存率预测
1. 提出问题
泰坦尼克号共2224个人,沉船后只有772人存活,生存率仅有32%。尝试建立机器学习模型,通过分析乘客的个人信息,预测个人的存活率,并用测试数据评测模型的预测准确率。
2. 数据处理
首先从网络上下载泰坦尼克号的训练数据与测试数据v。利用pd.read_csv将数据导入。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
import time
import warnings
import matplotlib as mpl
data_train=pd.read_csv("C:/Users/28555/Desktop/train.csv")
data_test=pd.read_csv("C:/Users/28555/Desktop/test.csv")3. 存活率可视化的实现
乘客的可用信息包括性别,年龄,客舱等,而我们的可视化分析主要就分析这三个方面,代码如下:
data_train_age = data_train[data_train['Age'].notnull()]
plt.figure(figsize=(8,3))
data_train_age['Age'].hist(bins=70)
plt.xlabel('Age')
plt.ylabel('Num')
plt.show()
bins = [0,6, 12, 20,39,59,100]
group_names = ['infant', 'child', 'teen',"prime","middle","old"]
data_train['categories'] = pd.cut(data_train['Age'], bins, labels = group_names)
mpl.rcParams['font.family']='DFKai-SB' # 修改了全局变量
plt.style.use('grayscale')
s_pclass= data_train['Survived'].groupby(data_train['categories'])
s_pclass = s_pclass.value_counts().unstack()
fig = s_pclass.plot(kind='bar',stacked = True, colormap='tab20c',title='mortality rate of age',fontsize=20)
fig.axes.title.set_size(20)
plt.show()
mpl.rcParams['font.family']='DFKai-SB' # 修改了全局变量
plt.style.use('grayscale')
s_pclass= data_train['Survived'].groupby(data_train['Pclass'])
s_pclass = s_pclass.value_counts().unstack()
s_sex = data_train['Survived'].groupby(data_train['Sex'])
s_sex = s_sex.value_counts().unstack()
fig = s_sex.plot(kind='bar',stacked = True, colormap='tab20c',title=' mortality rate of sex',fontsize=20)
plt.show()
fig = s_pclass.plot(kind='bar',stacked = True, colormap='tab20c',title='mortality rate of pclass',fontsize=20)
fig.axes.title.set_size(20)
fig,ax = plt.subplots(1,2, figsize = (9,4))
sns.violinplot("Pclass","Age",hue="Survived",data=data_train_age,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age",hue="Survived",data=data_train_age,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()
sns.countplot(x='SibSp',hue='Survived',data=data_train)
plt.show()
sns.countplot(x='Parch',hue='Survived',data=data_train)
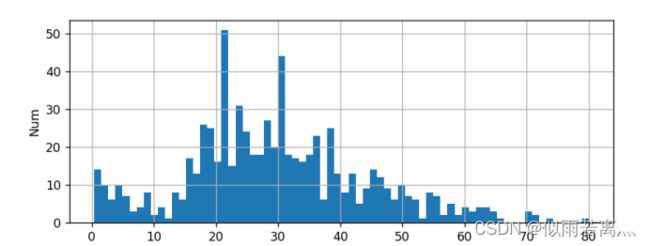
plt.show()具体代码的功能这里不一一赘述了,先对运行出来的图像进行分析。首先是画出所有乘客的年龄分布,如下图。可以看出乘客的年纪主要分布在20-40岁之间。
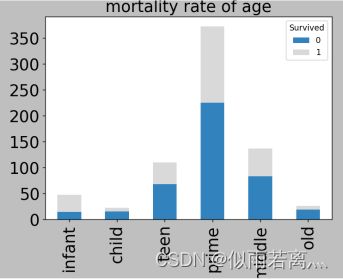
接着分析不同年龄的生存率,如下图。(0代表死亡,1代表生存)
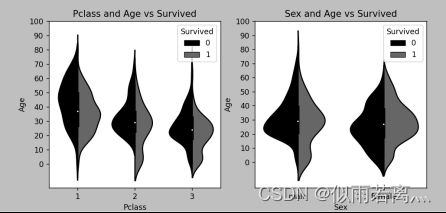
然后展示不同客舱和性别的乘客的生存情况,如下图:(0代表死亡,1代表生存)
最后,综合上述三种信息,综合起来得出展示,如图:(0代表死亡,1代表生存)
还有对家人数目的分析,如图:(0代表死亡,1代表生存)。作图代表父母子女数目与死亡率的关系,右图代表兄弟姐妹数与死亡率的关系。
经过上述可视化的分析,可以看出乘客的生存和死亡率与年龄,性别以及舱位等级等有较为密切的关系。对于年龄,我将不同年龄段的乘客进行了分类,分成了6组进行比较,发现婴儿的死亡率最低,而小孩和老人的死亡率最高;对于性别,可以看出男性的死亡率要远远高于女性;对于客舱等级,可以看出死亡率从1至3递减;对于家人数量,过少或过多都会导致死亡率的上升,兄弟姐妹和父母子女数量在1-2时,可以有效降低死亡率。综上所属,通过乘客的这些信息来预测一名乘客的死亡率是比较科学的,因此我们可以构建模型来进行预测。因此下面我就将构建一个机器学习模型。
4. 数据处理
数据之中存在很多空白之处,所以在构建模型之前首先我需要先填补空白。对于年龄(age),我直接将空白填为中位数,而对于上船的码头(embarked),我选择了最多的S。
data_train['Age']=data_train['Age'].fillna(data_train['Age'].median())#用年龄的中位数填充年龄空值
data_train['Embarked']=data_train['Embarked'].fillna('S')#Embarked缺失值用最多的‘S’进行填充由于性别(sex)和上船的码头(embarked)的数据都不是数字,无法进行处理,故我为其进行了赋值。对于性别,令男性(male)为0,女性(female)为1;对于上船的码头,令S=0,C=1,Q=2。
data_train.describe()
data_train.loc[data_train['Sex']=='male','Sex']=0
data_train.loc[data_train['Sex']=='female','Sex']=1
#Embarked处理:用0,1,2
data_train.loc[data_train['Embarked']=='S','Embarked']=0
data_train.loc[data_train['Embarked']=='C','Embarked']=1
data_train.loc[data_train['Embarked']=='Q','Embarked']=25. 模型构建
构建模型我们需要用到的参数包括客舱等级(Pclass),性别(Sex),年龄(Age),兄弟姐妹数(SibSp),父母子女数(Parch),船票价格(Fare)以及登船码头(Embarked)。然后利用逻辑回归函数LogisticRegression,在需要设置random_state的地方给其赋一个值,当多次运行此段代码能够得到完全一样的结果,别人运行此代码也可以复现你的过程。若不设置此参数则会随机选择一个种子,执行结果也会因此而不同了。虽然可以对random_state进行调参,但是调参后在训练集上表现好的模型未必在陌生训练集上表现好,所以一般会随便选取一个random_state的值作为参数。再用fit函数进行处理,最后交叉验证函数通过训练集(train)评估准确率的预测,并进行输出。
predictors=['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']
LogRegAlg=LogisticRegression(random_state=1)#初始化逻辑回归
re=LogRegAlg.fit(data_train[predictors],data_train['Survived'])
scores=model_selection.cross_val_score(LogRegAlg,data_train[predictors],data_train['Survived'],cv=5)#使用sklearn库里的交叉验证函数获取预测准确率分数
print("准确率为:")
print(scores.mean())6. 模型预测
接下来将对测试机(test)进行预测。首先还是如第四步那般对数据进行处理,补全空白并对性别和上船码头进行赋值,之后通过模型进行预测,构建“Survived”项,并进行输出。
data_test.describe()
data_test['Age']=data_test['Age'].fillna(data_test['Age'].median())
data_test['Fare']=data_test['Fare'].fillna(data_test['Fare'].max())
data_test.loc[data_test['Sex']=='male','Sex']=0
data_test.loc[data_test['Sex']=='female','Sex']=1
data_test['Embarked']=data_test['Embarked'].fillna('S')
data_test.loc[data_test['Embarked']=='S','Embarked']=0
data_test.loc[data_test['Embarked']=='C','Embarked']=1
data_test.loc[data_test['Embarked']=='Q','Embarked']=2
test_features=['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']
test_predictors=data_test[test_features]#构造测试集的survived列
data_test['Survived']=LogRegAlg.predict(test_predictors)
print('对测试人员的预测:')
print(data_test)7. 结果分析
之后观察输出,可以看出,经过机器学习,模型对预测结果的预测准确率可以达到79%
以上,准确率较高,对结果的乘客生存情况的预测也较为可靠,这也说明,泰坦尼克号乘客的生存情况与乘客的信息是由较多联系的,这个模型的设计也较为合理。当然,由于训练和测试数据都存在较多空白,只能由我自己定义,因此模型对乘客的生存情况的预测还是会有较大偏差。
8. 完整代码
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
import time
import warnings
import matplotlib as mpl
data_train=pd.read_csv("C:/Users/28555/Desktop/train.csv")
data_test=pd.read_csv("C:/Users/28555/Desktop/test.csv")
data_train_age = data_train[data_train['Age'].notnull()]
plt.figure(figsize=(8,3))
data_train_age['Age'].hist(bins=70)
plt.xlabel('Age')
plt.ylabel('Num')
plt.show()
bins = [0,6, 12, 20,39,59,100]
group_names = ['infant', 'child', 'teen',"prime","middle","old"]
data_train['categories'] = pd.cut(data_train['Age'], bins, labels = group_names)
mpl.rcParams['font.family']='DFKai-SB' # 修改了全局变量
plt.style.use('grayscale')
s_pclass= data_train['Survived'].groupby(data_train['categories'])
s_pclass = s_pclass.value_counts().unstack()
fig = s_pclass.plot(kind='bar',stacked = True, colormap='tab20c',title='mortality rate of age',fontsize=20)
fig.axes.title.set_size(20)
plt.show()
mpl.rcParams['font.family']='DFKai-SB' # 修改了全局变量
plt.style.use('grayscale')
s_pclass= data_train['Survived'].groupby(data_train['Pclass'])
s_pclass = s_pclass.value_counts().unstack()
s_sex = data_train['Survived'].groupby(data_train['Sex'])
s_sex = s_sex.value_counts().unstack()
fig = s_sex.plot(kind='bar',stacked = True, colormap='tab20c',title=' mortality rate of sex',fontsize=20)
plt.show()
fig = s_pclass.plot(kind='bar',stacked = True, colormap='tab20c',title='mortality rate of pclass',fontsize=20)
fig.axes.title.set_size(20)
fig,ax = plt.subplots(1,2, figsize = (9,4))
sns.violinplot("Pclass","Age",hue="Survived",data=data_train_age,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age",hue="Survived",data=data_train_age,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()
sns.countplot(x='SibSp',hue='Survived',data=data_train)
plt.show()
sns.countplot(x='Parch',hue='Survived',data=data_train)
plt.show()
data_train['Age']=data_train['Age'].fillna(data_train['Age'].median())#用年龄的中位数填充年龄空值
data_train['Embarked']=data_train['Embarked'].fillna('S')#Embarked缺失值用最多的‘S’进行填充
data_train.describe()
data_train.loc[data_train['Sex']=='male','Sex']=0
data_train.loc[data_train['Sex']=='female','Sex']=1
#Embarked处理:用0,1,2
data_train.loc[data_train['Embarked']=='S','Embarked']=0
data_train.loc[data_train['Embarked']=='C','Embarked']=1
data_train.loc[data_train['Embarked']=='Q','Embarked']=2
predictors=['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']
LogRegAlg=LogisticRegression(random_state=1)#初始化逻辑回归
re=LogRegAlg.fit(data_train[predictors],data_train['Survived'])
scores=model_selection.cross_val_score(LogRegAlg,data_train[predictors],data_train['Survived'],cv=5)#使用sklearn库里的交叉验证函数获取预测准确率分数
print("准确率为:")
print(scores.mean())
data_test.describe()
data_test['Age']=data_test['Age'].fillna(data_test['Age'].median())
data_test['Fare']=data_test['Fare'].fillna(data_test['Fare'].max())
data_test.loc[data_test['Sex']=='male','Sex']=0
data_test.loc[data_test['Sex']=='female','Sex']=1
data_test['Embarked']=data_test['Embarked'].fillna('S')
data_test.loc[data_test['Embarked']=='S','Embarked']=0
data_test.loc[data_test['Embarked']=='C','Embarked']=1
data_test.loc[data_test['Embarked']=='Q','Embarked']=2
test_features=['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']
test_predictors=data_test[test_features]#构造测试集的survived列
data_test['Survived']=LogRegAlg.predict(test_predictors)
print('对测试人员的预测:')
print(data_test)