卷积神经网络中卷积的OpenCL实现
卷积神经网络中卷积的OpenCL实现
==============================================================
目录
1、卷积
2、卷积与图像处理
3、卷积的OpenCL实现
4、总结
==============================================================
本文主要介绍深度学习中卷积,以及卷积核的OpenCL实现。
另外:新版对齐方式都没了,莫名其妙。
1、卷积
在CNN(Convolutional Neural Network, 卷积神经网络)中,卷积是个必不可少的部件,该网络也因卷积得名。CNN的卷积层中,有许多滤波器,这些滤波器也称为卷积核,用于卷积运算,提取数据特征,这些滤波器的系数由训练得到。
在数字信号处理中,信号x(n)经过系统,相当于信号与系统的冲激响应函数h(n)进行卷积,得到输出y(n),其定义如下式。
上式中的符号“*”是卷积的意思。
可以看出,信号x(n)经过系统,与冲击响应函数序列经过纵轴翻折过的序列对应相乘。
而在卷积神经网络中卷积操作的原理即卷积核与对应的点对应相乘,核心即是乘累加,
卷积的方式比较多,假定滤波器的滑动步长stride(用s表示),以及滤波器的填充方式(填充长度用p表示),原始特征图W*H(宽W,高H),滤波器的尺寸用K*K表示,则输出特征图的尺寸为
上式中括号为下取整。
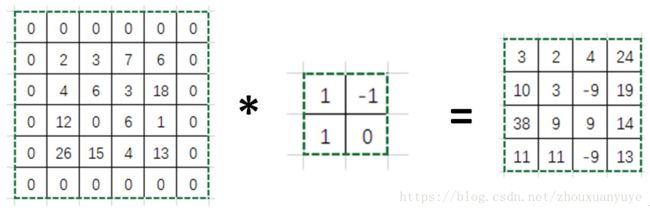
这个关系暂时没想通也没关系,可以搜索卷积神经网络卷积了解一下,卷积的核心即乘累加,如下为卷积图解。
图1. 卷积示例
上图中左侧为特征图与卷积核卷积,右侧为输出,其中卷积的步长stride为1,滤波器滑动方向先进行行处理,再进行列处理。
如右侧的最左上角的数 3= 2*1 + 3*(-1) + 4 + 6*0;
随后滤波器向右滑动1个单位,此时滤波器对应的数据为[3,7,6,3],所以3*1 + 7*(-1) + 6*1 +3*0 = 2,其他同理。
行处理完成,滤波器向下移动一个单位,接着处理下一行,此时与之对应的数为[4,6,12,0],所以4*1 + 6*(-1) + 12*1 + 0*0 = 10。其他同理。
图2. 特征图填充,卷积示例
图2中的卷积与图1不同在于,是否对原始特征图进行填充,填充可以保留特征图的边缘信息,不至于在卷积过程中丢失边缘信息。以上是其中一种填充方式,在特征图的周围环绕填充0,本例中忽略顶部及左侧的0值,保留右侧以及底层的边缘信息,使输出特征图大小与原始的特征图大小相等。
卷积以及更多填充方式的详细介绍可以参看如下链接:
Convolution arithmetic tutorial:
http://deeplearning.net/software/theano/tutorial/conv_arithmetic.html
A guide to convolution arithmetic for deep learning:
https://arxiv.org/pdf/1603.07285v1.pdf
2、卷积与图像处理
了解了卷积之后,如何在OpenCL中实现它呢?首先,一个单进程程序,使用一个卷积核对一张特征图进行处理,与多个并行进程,使用共享的卷积核对一张特征图进行处理相对比,显然后者计算速度快些。这就是加速,正是时代潮流上的加速。
假设有一个已经训练好的CNN网络用于识别著名的Lena,原始图片如下,宽高分别为W和H:
图 3. 名模Lena
卷积核如下,宽高均为K:
图 4. K*K卷积核
现对图片进行周围零填充,保持经过卷积后的输出图像与原始图像大小一致,假设保留右侧和底侧边缘信息,只对这两侧进行填充。(为什么保留右侧及底侧,其实如果你保留顶部和左侧边缘,又想输出图像大小一致,可能右侧和底侧的边缘信息也保留不了,在这我单纯只是为了好运算)。
图 5. 填充后的图大小(W+K-1)*(W+K-1)
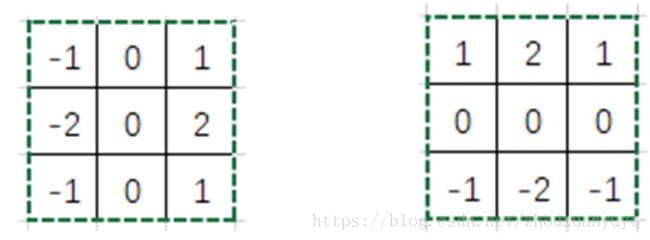
如果使用多个进程处理卷积操作,每个进程输入对应的滤波器系数和图像数据,对于每个进程,滤波器系数一致,可以共享;数据来自图像的不同位置,数据块大小为K*K。在深度学习中,训练完成的网络抽象了数据特征,得到不同特征的卷积核(滤波器),所以为了直观,本文将使用Sobel算子作为卷积核,K=3,可以用于图像边缘检测,生成边缘特征图。
Sobel算子的原理参考:
https://blog.csdn.net/qq_29540745/article/details/51918004
图 6. 水平梯度和垂直梯度卷积因子
3、卷积的OpenCL实现
Sobel算子与图像卷积的Matlab程序,我已放入Github中,如下:
https://github.com/yywyz/OpenCL-Programming-Examples/blob/master/CNN%20Convolution/Matlab%20src/sobel_conv.m
该代码与OpenCL中需要实现的卷积逻辑一致:
(1)图像数据与卷积核在存储器中是连续的,一维数组;
(2)输出特征图也是连续的一维数组。
图 7. Matlab输出水平梯度特征图
图 8. Matlab输出垂直梯度特征图
图 9. Matlab输出图像卷积图
在OpenCL中将使用W*H个工作项来完成卷积操作,工作项ID为(x, y),x和y取值分别为[0, W-1]和[0, H-1]。
滤波器的坐标值为(kj, ki),kj和ki取值范围均为[0, 1, 2]。
坐标为(kj, ki)卷积核对应的数据坐标示意图如下:
图 10. 滤波器坐标与图像数据坐标
所以,滤波器坐标(kj, ki)对应的存储索引值为[kj + K*ki];
图像数据对应的存储索引值为[( y + ki ) * Wn + x + kj],其中Wn=W+K-1;因为Matlab的首个数据索引为1,但在C语言中首个索引值为0,所以该处与上文Matlab代码中索引值略微不同。
以下为OpenCL的核函数Conv2D.cl:
https://github.com/yywyz/OpenCL-Programming-Examples/blob/master/CNN%20Convolution/Conv2D.cl
/**********************************************
function: 2D Convolution of CNN
date : 2018/07/21
**********************************************/
__kernel void Conv2D( __global int * image_in, //image input
__global int * filter_in, //filter input
int K, //filter kernel size
__global int * image_out) //feature map output
{
int W; //work group global size
int Wn; //padded image width
int x; //global id x
int y; //global id y
int ki, kj; //filter coordinate,(kj, ki)
int sum = 0; //multiply and sum of filter and data
W = get_global_size(0);
x = get_global_id(0);
y = get_global_id(1);
Wn = W + (K - 1);
for(ki=0; ki
OpenCL主函数main.cpp:
https://github.com/yywyz/OpenCL-Programming-Examples/blob/master/CNN%20Convolution/main.cpp
图 11. 随机数Sobel水平梯度卷积的结果显示
将输出图像导入到Matlab中显示即可作为验证,本代码中没有读取和生成图片功能,鉴于图片太大,存入内存太大,且只进行了水平梯度特征图对随机数的滤波,但已足以了解卷积的并行操作。如需处理文件,可将图片数据导入,输出文件已存于程序当前运行目录的image_out.txt中。
4、总结
本文介绍了卷积,卷积与图像处理,使用Sobel算子展示lena的水平梯度与垂直梯度的特征图,并通过OpenCL实现了卷积核,展示了使用Sobel水平梯度卷积核对随机数的卷积操作结果。
如有不当,请您斧正,谢谢。
途次客
2018年7月21日