临近期末，这些题不来看看吗？（下）

目录

1、打印1~100之间所有3的倍数（三种方法）

2、写出3给整数从大到小输出

3、给定两个数，求这两个数的最大公约数

4、 递归实现n的k次方

5、写一个递归函数DigitSum(n),输入一个非负整数，返回组成它的数字之和

6、编写一个函数 reverse_string(char * string)（非递归实现）

7、编写一个函数 reverse_string(char * string)（递归实现）

---

1、打印1~100之间所有3的倍数（三种方法）

法一：

让所有3的倍数与3求余都为0

#include 
int main()
{
	int i = 0;
	for (i = 1; i <= 100; i++)
	{
		if (i % 3 == 0)
			printf("%d ", i);
	}
	return 0;
}

法二：

让调整部分每次循环+3

int main()
{
	int i = 0;
	for (i = 3; i <= 100; i += 3)
	{
		printf("%d ", i);
	}
	return 0;
}

法三：

让条件判断部分每次*3

int main()
{
	int i = 0;
	for (i = 1; i * 3 <= 100; i++)
	{
		printf("%d ", i * 3);
	}
	return 0;
}

2、写出3给整数从大到小输出

#include 
int main()
{
	int a = 0;
	int b = 0;
	int c = 0;
	//输入
	scanf("%d %d %d", &a, &b, &c);
	//排序
	//最大放在a中，最小放在c中，剩余放在a中就行
	if (a < b)
	{
		int tmp = a;
		a = b;
		b = tmp;
	}
	if (a < c)
	{
		int tmp = c;
		c = a;
		a = tmp;
	}
	if (b < c)
	{
		int tmp = b;
		b = c;
		c = tmp;
	}
	
	//打印
	printf("%d %d %d", a, b, c);
	return 0;
}

3、给定两个数，求这两个数的最大公约数

法一：

解题思路：

首先最大公约数肯定不会超过两个数的最大值，所以先在a和b间找出最小值，再利用最小值分别对a、b求余，若两者余数都为0，说明就得到了最大公约数。

int main()
{
	int a = 0;
	int b = 0;

	//给定两个数
	scanf("%d %d", &a, &b);
	
	int k = (a > b ? b : a);//求a和b中最小值
	                                                //a     b
	while (1) //只要k不为0继续判断                   //18    24
	{												//18	18
		if (a % k == 0 && b % k == 0)				//17	17
		{											//6		6
			break; //a、b只要分别和k求余为0，就得到最大公约数
		}
		k--;
	}
	printf("%d ", k);

	return 0;
}

法二：

辗转相除法：

想了解辗转相除法可以看看这个链接：https://zhuanlan.zhihu.com/p/171623230

#include 
int main()
{
	int a = 0;
	int b = 0;
	int k = 0;
	scanf("%d %d", &a, &b);
	while (k = a % b)
	{
		a = b;
		b = k;
	}
	printf("%d\n", b);

	return 0;
}

4、 递归实现n的k次方

解题思路：

代码实现：

#include 
double Pow(int n, int k)
{
	if (k == 0)
	{
		return 1.0;
	}
	else if (k > 0)
	{
		return n * Pow(n, k - 1);
	}
	else //k<0
	{
		return 1.0 / Pow(n, -k);
	}

}
int main()
{
	int n = 0;
	int k = 0;
	//输入
	scanf("%d %d", &n, &k);
	double ret = Pow(n, k);
	printf("%Lf\n", ret);
	return 0;
}

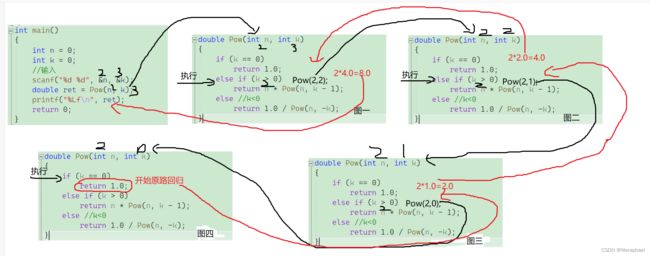
递归流程（画图）

递：递推（黑线）

归：回归（红线）

假设要计算2的3次方

5、写一个递归函数DigitSum(n),输入一个非负整数，返回组成它的数字之和

例如：调用DigitSum(1729)，则应该返回19

解题思路：

当n是一位数时，返回组成它的数字之和不就是n本身

当n是一位数以上时，可以想想是不是个位的数字非常好得到，只需让n%10即可，就举DigitSum(1729)可以传化成DigitSum(1729/10)+1729%10，接下来DigitSum(172/10)+172%10，这样以此类推下来不就是个递归吗

这题类似于按顺序打印每一位

https://blog.csdn.net/Weraphael/article/details/127831828

代码实现：

#include     
int DigitSum(int n)
{
	if (n <= 9) //若输入一位数，则返回对应的值
	{
		return n;
	}

	else //n>9
	{
		return DigitSum(n / 10) + n % 10;
	}
}
int main()
{
	int n = 0;
	//输入
	scanf("%d", &n);
	int ret = DigitSum(n);
	printf("%d\n", ret);
	return 0;
}

递归流程（画图）

递：递推（黑线）

归：回归（红线）

6、编写一个函数 reverse_string(char * string)（非递归实现）

实现：将参数字符串中的字符反向排列，不是逆序打印。
要求：不能使用C函数库中的字符串操作函数。
比如：char arr[]="abcdef"
逆序后数组内容变成：fedcba

解题思路：

代码实现： 

#include 
#include 
int Strlen(char* string)//计算字符串长度
{
	int count = 0;
	while (*string != '\0')
	{
		count++;
		string++;
	}
	return count;
}
void reverse_string(char* string)
{
	int left = 0;
	int right = Strlen(string) - 1;
	while (left <= right)
	{
		char tmp = string[left];
		string[left] = string[right];
		string[right] = tmp;
		left++;
		right--;
	}
}
int main()
{
	char arr[] = "abcdef";
	reverse_string(arr);
	printf("%s\n", arr);
	return 0;
}

程序结果：

 最后再给大家推荐一种写法

#include 
#include 
int Strlen(char* arr)//计算字符串长度
{
	int count = 0;
	while (*arr != '\0')
	{
		count++;
		arr++;
	}
	return count;
}
void reverse_string(char* arr)
{
	int left = 0;//左下标
	int right = Strlen(arr) - 1;//右下标
	while (left <= right)
	{
		char tmp = *(arr+left);
		*(arr + left) = *(arr+right);
		*(arr + right) = tmp;
		left++;
		right--;
	}
}
int main()
{
	char arr[] = "abcdef";
	reverse_string(arr);
	printf("%s\n", arr);
	return 0;
}

中间部分代码解析：

数组名是首元素的地址，对于形参的arr，其实就指向了a的地址，接着arr+left，而left一开始为0，加0等于没加还是指向a的地址， 最后再进行解引用，就找到了a。*(arr+right)也是如此。这种写法和一开始写的没差，主要是为了方便大家理解。

7、编写一个函数 reverse_string(char * string)（递归实现）

实现：将参数字符串中的字符反向排列，不是逆序打印。
要求：不能使用C函数库中的字符串操作函数。
比如：char arr[]="abcdef"

解题思路：

对于递归，可以拆成两步，第一步先交换a和f，第二步再调用reverse string(bcde)，来逆序bcde。然后呢reverse string(bcde)又能拆成两步，第一步交换b和e。第二步再调用reverse string(cd)，来逆序cd。接着reverse string(cd)又能拆成两步，第一步交换C和d，第二步调用reverse string(空字符串)，调用空字符串时就能回归了，大概思路就是这样。

代码实现： 

#include 
int Strlen(char* string)//计算字符串长度
{
	int count = 0;
	while (*string != '\0')
	{
		count++;
		string++;
	}
	return count;
}
void reverse_string(char* string)
{
	int len = Strlen(string);//求字符串长度
	//交换
	char tmp = *string;                //*string = a 
	*string = *(string + len - 1);     //*(string + len - 1) = f
	*(string + len - 1) = '\0';		   //防止递归乱套
	if (Strlen(string + 1) >= 2)       //防止死递归
	{
		reverse_string(string + 1);
	}
	
	*(string + len - 1) =  tmp;
	
}
int main()
{
	char arr[] = "abcdef";
	reverse_string(arr);
	printf("%s\n", arr);
	return 0;
}