python实现K-means聚类法对图片进行RGB颜色聚类，然后计算信息熵并对聚类后的颜色进行Huffman编码

问题描述

1、对一张给定的图片，使用python实现K-means聚类算法，对该图片的颜色进行聚类，需要给出聚类的个数
2、计算图片的信息熵，然后对其进行颜色聚类，最后对颜色进行Huffman编码，结果表示为 一个三列的表格，其中第一列为颜色RGB（或BGR）代码，第二列为该颜色出现的概率，第三列为对应颜色的Huffman编码。

---

K-means

将n个样本依据最小化类内距离的准则分到K个聚类中

算法的步骤是：
1、先随机选择K个初始的聚类中心
2、计算每个样本和这k个聚类中心的距离，按照最近原则将这些点分到这K个聚类中
3、重新计算每个聚类的均值，再进行划分
4、直到聚类结果没有变化时，算法收敛

K-means算法实现起来比较简单，空间和计算复杂度较低，经过有限步数就能够收敛得到聚类输出，但是最后的结果受初始聚类均值选择的影响，这有可能导致收敛于不同的局部极小解，而且这个算法需要预先设定聚类个数，这个在实际使用时很难判断

---

信息熵

信息熵：离散随机变量X的熵H(X)为：

图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。图像的一 维熵表示图像中灰度分布的聚集特征所包含的信息量，将图像的灰度值进行数学统计，便可得到每个灰度值出现的次数及概率，则定义灰度图像的一元灰度熵为：

利用信息熵的计算公式便可计算图像的信息熵，求出任意一个离散信源的熵（平均自信息量）。自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。所发出的消息不同，它们所含有的信息量也就不同。任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
信息熵的意义：信源的信息熵H是从整个信源的统计特性来考虑的。它是从平均意义上来表征信源的总体特性的。对于某特定的信源，其信息熵只有一个。不同的信源因统计特性不同，其熵也不同。
图像的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。选择图像的邻域灰度均值作为灰度分布的空间特征量，与图像的像素灰度组成特征二元组，记为( i, j )，其中i 表示像素的灰度值(0 <= I <= 255)，j 表示邻域灰度(0 <= j <= 255)

Huffman编码

huffman编码的具体方法：先按出现的概率大小排队，把两个最小的概率相加，作为新的概率 和剩余的概率重新排队，再把最小的两个概率相加，再重新排队，直到最后变成1。每次相 加时都将“0”和“1”赋与相加的两个概率，读出时由该符号开始一直走到最后的“1”， 将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好，就是该符号的赫夫曼编码。
平均码长：L=∑p(si)*li （单位为：码符号/信源符号）其中，p(si)为信源si在q个信源中出现的概率，li为信源si的二进制huffman编码。
编码效率：η= H(S)/ L 其中，H(S)为信息熵，L为平均码长。

对图片使用K-means算法对颜色进行聚类

先将图像数据展平，得到一个img.shape[0]*img.shape[1]行3列的矩阵，从中随机选取K个中心点颜色，创建一个bestAssignment矩阵用来保存每个像素点距离最近的中心点，接下来进入循环，另创建lastAssignment矩阵，让它初始化为bestAssignment，也就是上次循环后的结果，之后计算每个像素点与各中心点的距离，然后更新bestAssignment，当bestAssignment和lastAssignment元素相等时，也就是说前后两次循环结果没有改变时退出循环，如果不满足退出条件则先更新中心点的值，再次进入循环。

# K-means算法实现
def k_means(X, K):
    N, d = X.shape
    # 没有这步不行，因为图像的数据类型为uint8
    X = X.astype(np.int32)
    temp = np.arange(N)
    np.random.shuffle(temp)
    C = X[temp[:K]]

    bestAssignment = np.zeros((N, 1), dtype=np.int32)

    while True:
        lastAssignment = bestAssignment.copy()
        #
        mindist = np.inf * np.ones((N, 1))
        for k in range(K):
            for n in range(N):
                dist = np.sum((X[n, :] - C[k, :]) ** 2)
                if dist < mindist[n]:
                    mindist[n] = dist
                    bestAssignment[n] = k

        if all(bestAssignment == lastAssignment):
            break

        for k in range(K):
            index = np.where(bestAssignment == k)
            C[k, :] = np.mean(X[index[0], :], axis=0)
            # print(C)

    return bestAssignment.squeeze(), C

---

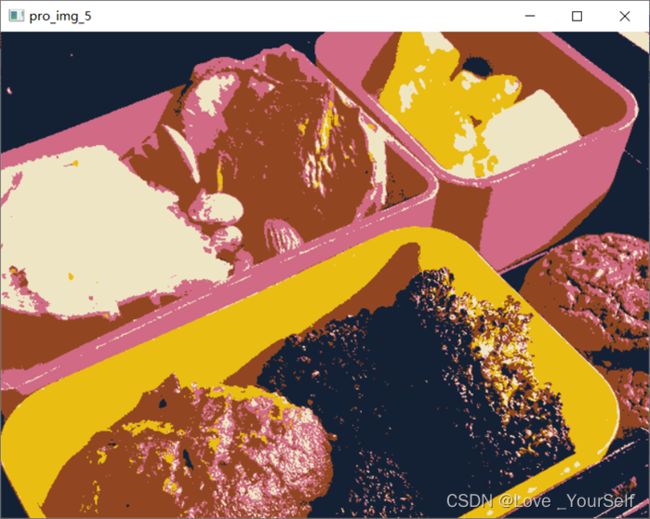
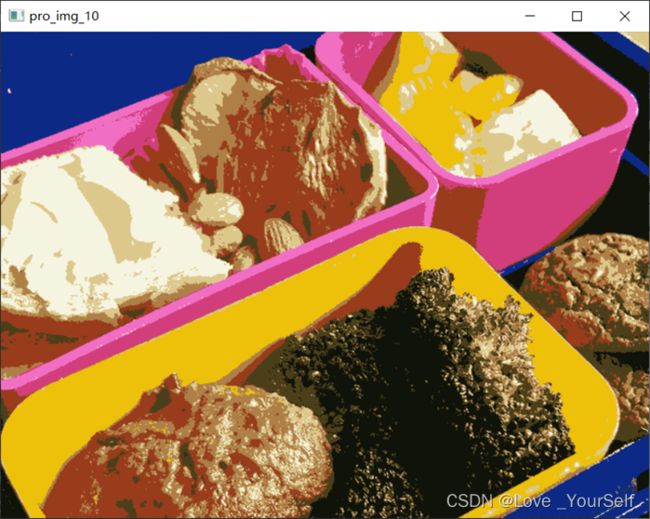
效果展示

通过将K设置为2，3，5，10可以得到如下的结果，据图可知K越大此时聚类越多色彩越丰富，同时程序运行的时间也会明显增加。

---

计算信息熵和huffman编码

上图只是展示聚类结果，这里计算信息熵和huffman编码时使用的是其他图片。因为一张图片的颜色可能会很多，所以我先使用上述的k-means算法对颜色进行聚类，这里我就选择10个类别吧，之后利用公式计算图像颜色的信息熵。

def calculate_p(img):
    result_dic = {}
    line = img.shape[0]
    row = img.shape[1]
    num = img.shape[0] * img.shape[1]
    H = 0.0

    # 得到每个颜色的数量
    for i in range(line):
        for j in range(row):
            if str(img[i][j]) in result_dic:
                result_dic[str(img[i][j])] += 1.0
            else:
                result_dic[str(img[i][j])] = 1.0

    for key, value in result_dic.items():
        result_dic[key] = value / num
        value /= num
        H += -value * (math.log2(value))

    return result_dic, H

然后计算各颜色的huffman编码，它具体方法的是先按出现的概率大小排队，把两个最小的概率相加，作为新的概率 和剩余的概率重新排队，再把最小的两个概率相加，再重新排队，直到最后变成1。每次相加时都将“0”和“1”赋与相加的两个概率，读出时由该符号开始一直走到最后的“1”，将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好，就是该符号的赫夫曼编码，最后得到的结果用pandas进行处理后可以显示为下面图片中的结果，出现概率越大的颜色，其编码的码长越短。
之后再计算以Huffman编码后图片平均每个像素所需要的bit数，压缩率和文件占用空间，在计算编码后每个像素所需要的bit数时，只需用各颜色的编码码长乘对应颜色出现的概率，然后进行加和，最后需要向上取整。接着计算压缩率，每个像素由原来24减少到了3，所以压缩率为（24-3）/24，结果为87.5%。然后计算原图和编码后的文件大小，这里使用每个像素的大小乘以图像的大小，结果可知经过编码后的文件大小要远小于原图。

计算huffman编码的关键函数

# 输入节点构造哈夫曼树的函数
def createHuffmanTree(nodes):
    queue = nodes[:]
    while len(queue) > 1:
        queue.sort(key=lambda item: item.freq)
        node_left = queue.pop(0)
        node_right = queue.pop(0)
        node_father = Node(node_left.freq + node_right.freq)
        node_father.left = node_left
        node_father.right = node_right
        node_left.father = node_father
        node_right.father = node_father
        queue.append(node_father)
    queue[0].father = None
    return queue[0]

---

结果展示