UVA LIVE-4642 - Malfatti Circles
给出三角形三个顶点,求出三个互切的圆的半径
尽管大白鼠说能够推出公式,但是这个公式仅仅怕没那么easy推……我左看右看上看下看也推不出。
应该是要做辅助线什么的,那也……
因为非常easy就推出了关于三个半径的三元方程组,那么就试试搜索吧,搜当中随意一个半径,仅仅要满足这个方程组就能够了,
那么就二分搜索吧,当然,这个单调性呢?
看图可知,例如说,我们搜最靠近最上面的顶点的圆的半径r1,由于,以下两圆的r2,r3都是由r1推出,由于方程组的约束作用,那么以下两个圆肯定跟最上面的圆相切,当然也肯定跟三角形的边相切,可是这两个圆之间可不一定相切了,假设r1太大,那么这两个圆肯定相离,由它们两推出的底边肯定就小了,假设r1太小,那么这两个圆肯定相交,由它们两推出的底边肯定就大了。好的,有单调性,也就是说,r1跟底边长度是单调递减的关系。
r1的下界就是0,上界却不能太大,由于太大,r2,r3就木有了,就是说方程组是无法通过r1推出满足的r2,r3的,带到方程组里是会出问题的,所以,r1不能太大,那么多大合适呢?列出方程组就非常easy知道了。
这是大白鼠的计算几何Basic部分的最后一题,那么这个部分就圆满结束了。通过这个部分,解析几何的能力有所提升。
我的代码:
#include<iostream>
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
const double eps=1e-7;
struct dot
{
double x,y;
dot(){}
dot(double a,double b){x=a;y=b;}
dot operator -(const dot &a){return dot(x-a.x,y-a.y);}
double mod(){return sqrt(pow(x,2)+pow(y,2));}
double dis(const dot &a) {return sqrt(pow(x-a.x,2)+pow(y-a.y,2));}
double mul(const dot &a) {return x*a.x+y*a.y;}
};
int main()
{
bool flag;
int i,j;
dot a[3],c[3];
double l,h,m,b[3],e[3],r[3],A,B,C;
while(1)
{
flag=1;
for(i=0;i<3;i++)
{
cin>>a[i].x>>a[i].y;
if(a[i].x!=0||a[i].y!=0)
flag=0;
}
if(flag)
break;
for(i=0;i<3;i++)
{
c[0]=a[(i+1)%3]-a[i];
c[1]=a[(i+2)%3]-a[i];
b[i]=acos(c[0].mul(c[1])/c[0].mod()/c[1].mod())/2;
}
e[0]=a[0].dis(a[1]);
e[1]=a[1].dis(a[2]);
e[2]=a[0].dis(a[2]);
l=0;
h=min(e[0]*tan(b[0]),e[2]*tan(b[0]));
while(h-l>eps)
{
m=(l+h)/2;
A=1/tan(b[1]);B=2*sqrt(m);C=m/tan(b[0])-e[0];
r[0]=(sqrt(B*B-4*A*C)-B)/A/2;
A=1/tan(b[2]);B=2*sqrt(m);C=m/tan(b[0])-e[2];
r[1]=(sqrt(B*B-4*A*C)-B)/A/2;
r[0]*=r[0];
r[1]*=r[1];
if(r[0]/tan(b[1])+r[1]/tan(b[2])+2*sqrt(r[0]*r[1])-e[1]>0)
l=m;
else
h=m;
}
printf("%.6lf %.6lf %.6lf\n",l,r[0],r[1]);
}
}原题:
Time limit: 3.000 seconds
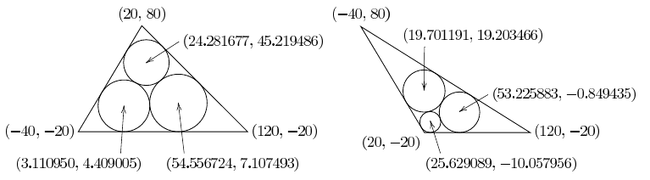
- the circle with the center (25.629089, -10.057956) and the radius 9.942044,
- the circle with the center (53.225883, -0.849435) and the radius 19.150565, and
- the circle with the center (19.701191, 19.203466) and the radius 19.913790.
Your mission is to write a program to calculate the radii of the Malfatti circles of the given triangles.
Input
The input is a sequence of datasets. A dataset is a line containing six integers x1, y1, x2, y2, x3 and y3 in this order, separated by a space. The coordinates of the vertices of the given triangle are (x1, y1), (x2, y2) and (x3, y3), respectively. You can assume that the vertices form a triangle counterclockwise. You can also assume that the following two conditions hold.
- All of the coordinate values are greater than -1000 and less than 1000.
- None of the Malfatti circles of the triangle has a radius less than 0.1.
The end of the input is indicated by a line containing six zeros separated by a space.
Output
For each input dataset, three decimal fractions r1, r2 and r3 should be printed in a line in this order separated by a space. The radii of the Malfatti circles nearest to the vertices with the coordinates (x1, y1), (x2, y2) and (x3, y3) should be r1, r2 and r3, respectively.
None of the output values may have an error greater than 0.0001. No extra character should appear in the output.
Sample Input
20 80 -40 -20 120 -20 20 -20 120 -20 -40 80 0 0 1 0 0 1 0 0 999 1 -999 1 897 -916 847 -972 890 -925 999 999 -999 -998 -998 -999 -999 -999 999 -999 0 731 -999 -999 999 -464 -464 999 979 -436 -955 -337 157 -439 0 0 0 0 0 0
Sample Output
21.565935 24.409005 27.107493 9.942044 19.150565 19.913790 0.148847 0.207107 0.207107 0.125125 0.499750 0.499750 0.373458 0.383897 0.100456 0.706768 0.353509 0.353509 365.638023 365.638023 365.601038 378.524085 378.605339 378.605339 21.895803 22.052921 5.895714