基于统一空间方法的动态切换拥挤（DSC）DSC-MOAGDE算法附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

本研究提出了一种稳健的方法，使用基于帕累托的归档机制和基于拥挤距离的归档处理机制来提高多目标进化算法 (MOEA) 的搜索性能。所提出方法的目的是在目标和决策空间中提供可持续的多样性，并在两个空间中建立稳定的开发-探索平衡。为此：1) 定义了参考空间组合，2) 开发了由参考空间组合组成的策略以提高拥挤距离计算的性能，以及 3) 提出了一种动态切换机制来实现这些策略。在所提出的 DSC 方法中，非支配解在三个不同的参考空间中表示：决策空间、目标空间、以及这两个空间的统一结果。创建了这三个空间的二进制组合，并开发了使用不同参考空间的策略。切换机制旨在动态地实施这些策略。参考由该切换机制选择的空间向量执行拥挤距离计算。所提出的 DSC 方法在多模态多目标优化问题 (MMOP) 和结合交流最优功率流 (AC-OPF) 和交流/直流最优功率流 (AC/DC-OPF) 的实际工程问题上进行了测试. 根据实验研究结果，与竞争对手相比，所提出的 DSC-MOAGDE 算法在 MMOP 上的成功率提高了约 30%。同样，所提出的方法能够将成本优化 6.66%、24.15%、52。

⛄ 部分代码

function [bestFitness]=MOAGDE_SingerMap_Cr3(NP,funnum)

[fname,D, n_obj, L, H] = terminate_problem(funnum);

GEN = 50;

problemName = strcat("@",fname);

ObjectiveFunction=eval(problemName);

X = zeros(D,1); % trial vector

Pop = zeros(D,NP); % population

Fit = zeros(NP,n_obj); % fitness of the population

r = zeros(3,1); % randomly selected indices

Archive_member_no = 0;

bestFitness=inf*ones(1,n_obj);

Archive_X=zeros(NP,D);

Archive_F=ones(NP,n_obj)*inf;

ArchiveMaxSize = NP;

% *********************** %

% ** CREATE POPULATION ** %

% *********************** %

for j = 1:NP % initialize each individual

    Pop(:,j) = L + (H-L).*rand(1,D); % within b.constraints

end

Cr_All=zeros(1,2);

NW=zeros(1,2);

global chaosMap

SingerMap(GEN+10)

for g = 1:GEN % for each generation

    

    for i=1:NP %Calculate all the objective values first

        Fit(i,:)=ObjectiveFunction(Pop(:,i)');

        if dominates(Fit(i,:),bestFitness)

            bestFitness=Fit(i,:);

        end

    end

    

    [Archive_X, Archive_F, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, Pop', Fit, Archive_member_no);

    

    if Archive_member_no>ArchiveMaxSize

        Archive_X_F = [Archive_X Archive_F];

        Norm_Archive_X_F = Normalize(Archive_X_F);

        Norm_Archive_X = Normalize(Archive_X);

        if(rand()>chaosMap(g))

             Archive_mem_ranks_X=RankingProcess(Norm_Archive_X, ArchiveMaxSize, D);

            [Archive_X, Archive_F, ~, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks_X, ArchiveMaxSize);

        else

            Archive_mem_ranks_X_F=RankingProcess(Norm_Archive_X_F, ArchiveMaxSize, (n_obj+D));

            [Archive_X, Archive_F, ~, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks_X_F, ArchiveMaxSize);

       end    

    end

    

    Norm_Archive_X = Normalize(Archive_X);

    Archive_mem_ranks_X=RankingProcess(Norm_Archive_X, Archive_member_no, D);

    index=RouletteWheelSelection(1./Archive_mem_ranks_X);

    if index==-1

        index=1;

    end

    % Update the best Organism

    bestSolution=Archive_X(index,:);

    bestFitness=Archive_F(index,:);

    

    Norm_Archive_F = Normalize(Archive_F);

    Archive_mem_ranks_F=RankingProcess(Norm_Archive_F, Archive_member_no, n_obj);

    

    Norm_Fit = Normalize(Fit);

    allRank=RankingProcess(Norm_Fit, ArchiveMaxSize, n_obj);

    

    CrPriods_Index=zeros(1,NP);

    Sr=zeros(1,2);

    CrPriods_Count=zeros(1,2);

    for j = 1:NP % for each individual

         

         %%%%%%%%ADAPTIVE CR RULE  %%%%%%%%%%%%%%%%%%%%%%%%%

            Ali = rand;

            if(g<=1) % Do for the first Generation

                if (Ali<=1/2)

                    CR=0.05+0.1*rand(1,1);

                    CrPriods_Index(j)=1;

                

                else

                    CR=0.9+0.1*rand(1,1);

                    CrPriods_Index(j)=2;    

                end

                CrPriods_Count(CrPriods_Index(j))=CrPriods_Count(CrPriods_Index(j)) + 1;

            else

                 if (Ali<=NW(1))

                    CR=0.05+0.1*rand(1,1);

                    CrPriods_Index(j)=1;

                

                 else

                    CR=0.9+0.1*rand(1,1);

                    CrPriods_Index(j)=2;    

                end

                CrPriods_Count(CrPriods_Index(j))=CrPriods_Count(CrPriods_Index(j)) + 1;

            end

            %%%%%%%%%%%%%%%%%END OF CR RULE%%%%%%%%%%%%%%%%%%%%%%%%%%%

                indexs_Archive = [];

                while(size(indexs_Archive) < 3)

                    index=RouletteWheelSelection(1./Archive_mem_ranks_F);

                    if ismember(index,indexs_Archive) == 0

                        indexs_Archive = [indexs_Archive index];

                    end

                end

                

                indexs_Pop = [];

                while(size(indexs_Pop) < 3)

                    index=RouletteWheelSelection(1./allRank);

                    if ismember(index,indexs_Pop) == 0

                        indexs_Pop = [indexs_Pop index];

                    end

                end

                

                r(1) = indexs_Pop(1);

                r(2) = indexs_Archive(1);

                r(3) = indexs_Pop(2);

                F=0.1+0.9*rand(1,1);

                Archive_Pop = Archive_X';

                Rnd = floor(rand()*D) + 1;

                for i = 1:D

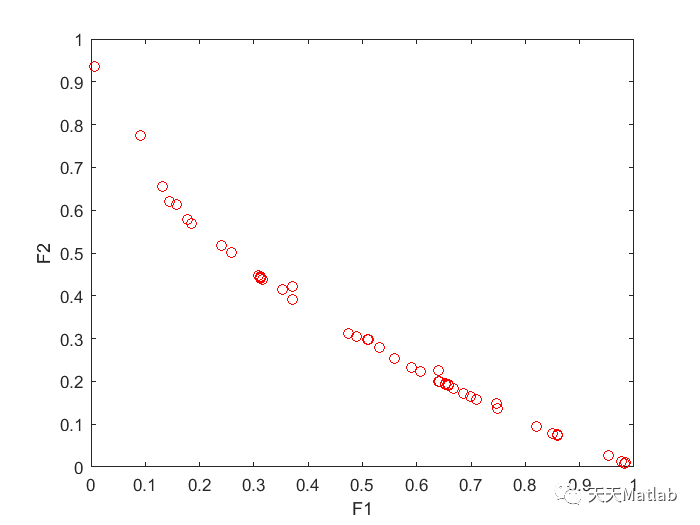
                    if ( rand()

                        X(i)=Pop(i,r(3))+F*(Pop(i,r(1))-(Archive_Pop(i,r(2))));

                    else

                        %X(i) = Pop(i,j);

                        X(i) = bestSolution(i);

                    end

                end

        % end%end of All cases

        % verify boundary constraints

        % verify boundary constraints

        for i = 1:D

            if (X(i)H(i))

                X(i) = L(i) + (H(i)-L(i))*rand();

            end

        end

        % select the best individual

        % between trial and current ones

        % calculate fitness of trial individual   

        XPf=ObjectiveFunction(X');

        % if trial is better or equal than current

        % CRRatio(find(A==CRs(j)))=CRRatio(find(A==CRs(j)))+1-(min(f,Fit(j))/max(f,Fit(j)));

        Sr (CrPriods_Index(j)) = Sr(CrPriods_Index(j)) +1;

        Pop(:,j) = X; % replace current by trial

        Fit(j,:) = XPf ;

        % if trial is better than the best

    end

    CrPriods_Count(CrPriods_Count==0)=0.0001;

    Sr=Sr./CrPriods_Count;

%%%%%%%%%%%%%%%%USING SR ONLY%%%%%%%%%%5    

    if(sum(Sr)==0)

        W=[1/2 1/2];

    else

        W=Sr/sum(Sr);

    end

    

%%%%%%%%%%%%%%%%%%%%%%%%%%5

    NW=(NW*(g-1)+W)/g;

    Cr_All=Cr_All+CrPriods_Count;

    display(['At the iteration ', num2str(g), ' best fitness ', num2str(bestFitness)]);

    

end

end

⛄ 运行结果

⛄ 参考文献

KAHRAMAN, H. T., AKBEL, M., DUMAN, S., KATI, M., SAYAN, H. H. (2022). Unified Space Approach-based Dynamic Switched Crowding (DSC): A New Method for Designing Pareto-based Multi/Many-Objective Algorithms, Swarm and Evolutionary Computation, 101196, https://doi.org/10.1016/j.swevo.2022.101196

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料