Python应用之求100以内的奇数和

在数学中，我们需要用到很多求和的办法，比如说求1至100的和，还有100以内的所有偶数和和所有奇数和，如果我们慢慢地计算是不是很浪费时间，还容易出错。其实通过Python就可以很好的实现，不仅速度快正确率还高。

1.解题的思路

对100以内的奇数求和，有四种常见的解题方法：

• 用range函数遍历100以内的奇数，然后用sum函数求和

• for 循环嵌套if语句，将100以内的奇数相加求和

• while循环将100以内的奇数相加，并打印求和

• 用递归方法求和

2.解题方法

方法一： sum函数

print(sum(range(1, 100, 2)))

首先用range函数创建了一个整数列表，range(1, 100, 2)表示取值为1-100(不包括100)的整数，步长为2，输出的值为1，3，5……99

更多关于range函数的用法查看Python应用之九九乘法表_9月月更_向阳逐梦_InfoQ写作社区

然后用sum函数对100以内的奇数求和最后用print函数将求和结果打印出来

这行代码充分体现了Python 语言的简洁性！！！

代码运行效果：

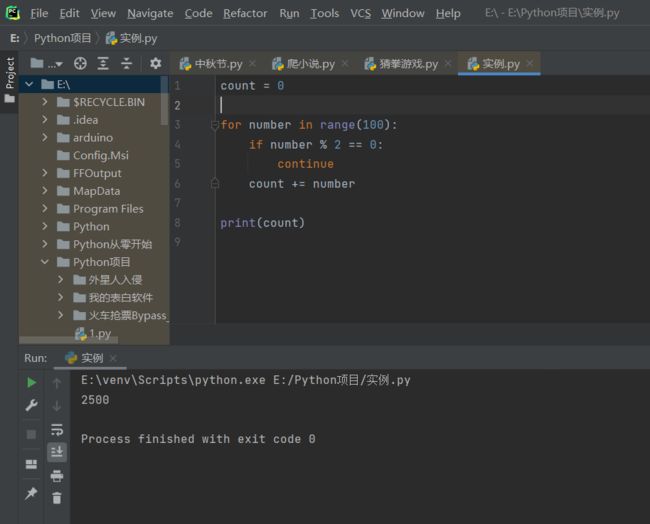
方法二：for循坏

count = 0

for number in range(100):
    if number % 2 == 0:
        continue
    count += number
    
print(count)

第1行： 设置一个变量count, 初始赋值为0

第3行： 用for循环遍历100以内所有的整数

第4-6行： 用if语句判断100以内的数是否为奇数，是奇数就相加（if i % 2 == 0,continue的含义是当数字为偶数时退出本次循环）

第8行： 用print函数打印其和

代码运行效果：

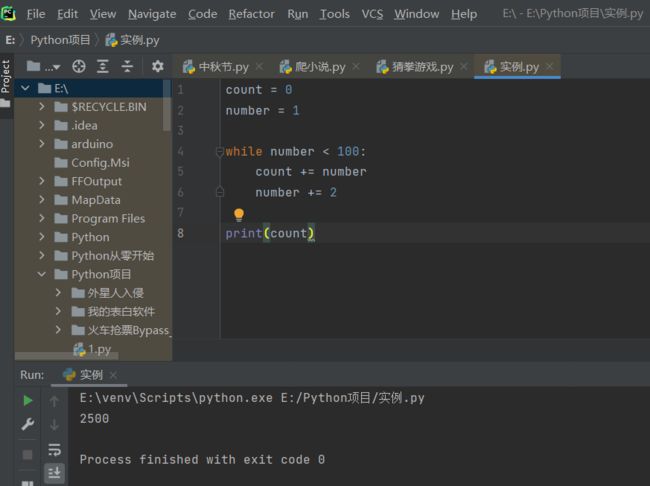
方法三：while循坏

count = 0
number = 1

while number < 100:
    count += number
    number += 2
    
print(count)

第1-2行： 设置一个变量count ,初始赋值为0，变量number初始赋值为1

第4-6行： 设定while循环的运行条件(number < 100)及执行语句（count += number；number += 2）第8行： 用print函数打印其和

代码运行效果：

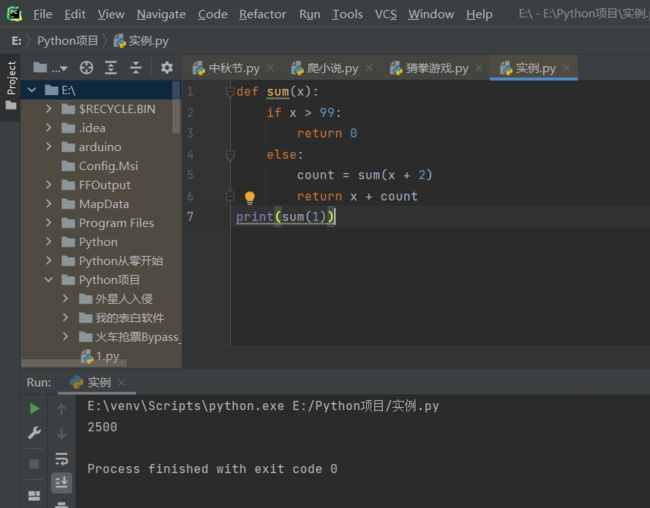
方法四：递归求和

def sum(x):
    if x > 99:
        return 0
    else:
        count = sum(x + 2)
        return x + count
print(sum(1))

先看下什么是递归：

递归（Recursion）递归是一种解决问题的思路，其精髓在于将问题分解为规模更小的相同问题，直到问题规模小到可以用非常简单直接的方式来解决，其算法方面的明显特征就是：在算法流程中调用自身。

也可以说在函数内部调用自己的函数被称之为递归

递归算法三定律：

• 必须要有结束条件（最小规模问题的直接解决）

  必须能向结束条件演进（减小问题规模）

  必须调用自身（解决减小了规模的相同问题）

在这段代码中，

第1行： 用def定义 sum 函数，传入参数 x

第2-3行： 设定这个设定递归算法的结束条件（if x > 99，return 0）

第4-6行： 在算法流程中调用sum函数自身，通过 return函数执行语句

第7行： 为x赋值为1，用print函数打印运算结果

代码运行效果：