常用特征选择

数据处理 - 常用特征选择方法

特征选择对于数据科学家、已经机器学习有关研究人员非常重要，通过减少特征数量、增加模型泛化能力，减少过拟合，能够增加特征之间的理解，降低学习任务的难度，提升模型的效率。常用的特征选择法分为：

1. 过滤式（filter）

通过一定的统计方法对每个特征进行评分排序，然后按照一定的规则过滤出最优的特征子集，然后在训练学习器，由于过滤不需要考虑后续的学习器，因此计算性能更好，常见的方法有 Relief/方差选择法/相关系数法/卡方检验法/互信息法；
思维导图如下：

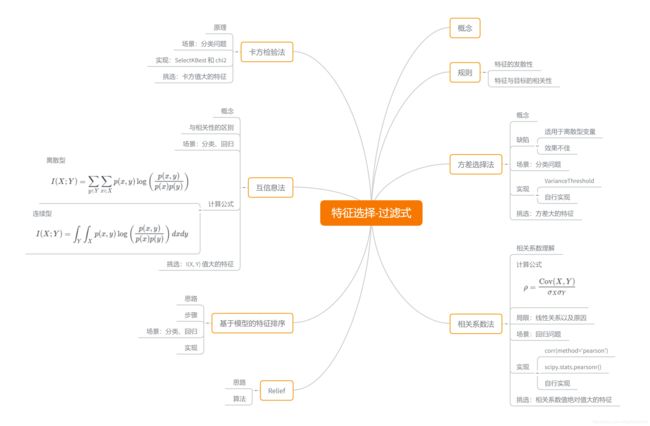
图片来源：https://blog.csdn.net/weixin_43378396/article/details/90649064

1.1 方差选择法

思路：计算各个特征的方差，根据阈值选择特征；或指定待选择的特征数k，选择方差最大的k个特征。

>>> from sklearn.feature_selection import VarianceThreshold
>>> X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
>>> sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
>>> sel.fit_transform(X)
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

优点：

• 简单、计算速度快

缺点：

• 对噪声和outlier非常不鲁棒
• 只针对离散变量，连续变量需要离散化
• 特征的方差仅只考虑自身的取值，没有考虑特征与目标变量的相关性，特征变量可能跟目标变量毫无关系

1.2 相关系数法

计算各个特征对目标值的相关系数及相关系数的P值，在机器学习中，皮尔逊系数只能检测出线性关系，因此更适用于回归问题
使用Pearson相关系数需要满足的条件：

• 两个变量间有线性关系
• 变量是连续变量
• 变量均符合正态分布
• 两变量独立
• 两变量的方差不为0

DataFrame.corr(method='pearson', min_periods=1)

参数说明：

method：{‘pearson’, ‘kendall’, ‘spearman’}

	pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，即针对线性数据的相关系数计算，                                           数据便会有误差。

	kendall：用于反映分类变量相关性的指标，即针对无序序列的相关系数，非正太分布的数据

	spearman：非线性的，非正太分析的数据的相关系数

min_periods：样本最少的数据量

常常我们分析的变量是不满足正态分布的，此时可以采用Spearman 或者 Kendall 相关系数来代替；
如果两个变量是非线性相关的，可以通过将特征进行非线性变化后，使之与目标线性相关；
Pearson系数对异常值较敏感，清洗阶段需要将异常值过滤或平滑处理。

1.3 卡方检验法

卡方检验主要是用来进行分类变量（离散变量） 的关联性、相关性分析，其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

H0：两个变量独立无关
H1：变量间有相互关联

卡方检验的公式为：

自由度df = (行数 - 1) * (列数 - 1)

>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectKBest
>>> from sklearn.feature_selection import chi2
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
>>> X_new.shape
(150, 2)

优点：不仅适用于二分类，还适用于多分类情况
缺点：只适用于离散变量

1.4 互信息法

互信息法与卡方检验法相同，都是评价定性自变量对定性因变量的相关性。互信息用以计算两个特征或自变量与因变量之间所共有的信息。

区别：互信息计算的不是数据序列，而是数据的分布，因此互信息可以用于检测特征间的非线性关系

互信息计算公式：

• 离散型
  
• 连续型

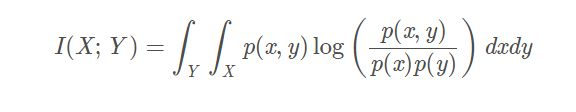
根据公式可以看出，若 X 与 Y 完全独立，则 p(X, Y) = p(X)p(Y)，I(X, Y) = 0。也就是说 I(X, Y) 越大，则表明 X 与 Y 的相关性越大

#回归问题
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.datasets import load_boston

dataset_boston = load_boston()
data_boston = dataset_boston.data
target_boston = dataset_boston.target

model_sk = SelectKBest(score_func=mutual_info_regression, k=4)
model_sk.fit(data_boston, target_boston)
print(model_sk.scores_)
# 输出
array([0.34945217, 0.18259661, 0.47229519, 0.0209894 , 0.46333988,
       0.52746991, 0.31724869, 0.29427874, 0.22223963, 0.35585112,
       0.45497479, 0.16204564, 0.66418786])

#分类问题
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_classif
from sklearn.datasets import load_iris

dataset_iris = load_iris()
data_iris = dataset_iris.data
target_iris = dataset_iris.target

model_sk = SelectKBest(score_func=mutual_info_classif, k=2)
model_sk.fit(data_iris, target_iris)
print(model_sk.scores_)
# 输出
array([0.48850984, 0.25341124, 0.9957628 , 0.97604533])

1.5 基于模型的特征排序

针对单独的特征和预测值直接建立预测模型

【步骤】

1. 判断特征值与预测值之间的关系，若为线性则建立线性算法；若为非线性则考虑非线性算法（eg. 树模型）
2. 单独采用每个特征进行建模，并进行交叉验证
3. 选择指定个数评分最高的特征，组成特征子集

1.6 Relief & ReliefF 算法

1.6.1 Relief 算法

Relief是一种特种权重算法，根据各个特征和类别的相关性赋予特征不同的权重，权重小于阈值的特征可以移除。

【思路】Relief算法中，特征和类别的相关性是基于特征对及距离样本的区分能力。算法从训练集D中随机选择一个样本R，

• 从和R同类的样本中寻找最近邻样本H，成为Near Hit；
• 从和R不同类样本中寻找最近邻样本M，成为Near Miss；

如果在某个特征上，Near Hit < Near Miss，该特征对分类起负面作用，降低该特征权重，反之增加权重

重复m此过程m次，得到每个特征的平均权重，权重越大，表示该特征分类能力越强。

【伪代码】

【优点】运行效率高，效果好
【缺点】仅能处理二分类问题

1.6.2 ReliefF 算法

Relief为一系列算法，它包括最早提出的Relief以及后来拓展的ReliefF和RReliefF，其中RReliefF算法是针对目标属性为连续值的回归问题提出的，下面仅介绍一下ReliefF算法。

【思路】ReliefF算法在处理多类问题时，每次从训练样本集中随机取出一个样本R，然后从和R同类的样本集中找出R的k个近邻样本(near Hits)，从每个R的不同类的样本集中均找出k个近邻样本(near Misses)，然后更新每个特征的权重

【伪代码】

【优点】运行效率高，对数据类型没有限
【缺点】不能有效的去除冗余特征

参考链接：https://blog.csdn.net/ferrarild/article/details/18792613

2. 包裹式（wrapper）

包裹式从初始特征集合中不断的选择特征子集，训练学习器，根据学习器的性能来对子集进行评价，直到选择出最佳的子集。

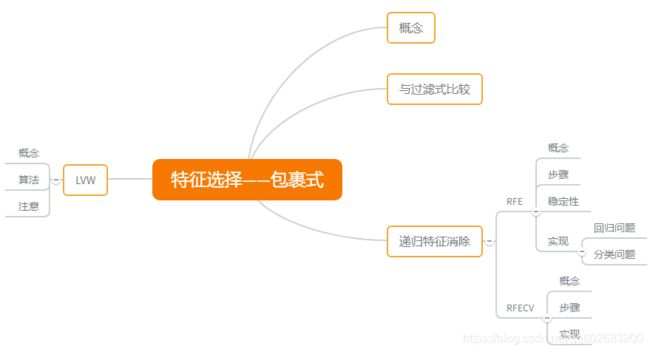
参考链接：https://blog.csdn.net/weixin_43378396/article/details/90647321

【与过滤式选择的区别】：
过滤式选择方法在模型训练之前，根据特征自身或与其他变量的数值上的关系进行变量选择，而包裹式选择方法直接针对给定学习器进行优化

【优点】
从最终学习器性能来看，包裹式选择比过滤式选择更好；

【缺点】
但另一方面，由于在特征选择过程中需多次训练学习器，因此包裹式选择的计算开销通常比过滤式选择大得多。

2.1 特征递归消除（Recursive Feature Elimination，RFE）

【思路】
特征递归消除是使用一个基模型进行多轮训练，RFE通过递归减少权重较小的特征，直至剩余特征达到指定特征数

【sklearn 官方解释】：对特征含有权重的预测模型，RFE 通过递归减少待考察特征集规模来选择特征。

首先，预测模型在原始特征集上进行训练，通过 coef_ 属性或 feature_importances_ 属性为每个特征指定一个权重；
然后，剔除那些权重绝对值较小的特征；
如此循环，直到剩余的特征数量达到所需的特征数量。

需要注意的是，RFE 的稳定性很大程度上取决于迭代时，底层使用的预测模型。如果 RFE 采用的是普通的逻辑回归，没有经过正则化的回归是不稳定的，因此 RFE 也不稳定。若采用的是脊回归 Ridge 或 Lasso，则 RFE 稳定。

from sklearn.feature_selection import RFE
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge

def ref_select(X_train,y_train,features_num,step):
    rfe = RFE(estimator = Ridge(), n_features_to_select = features_num,step=1))#step每次删除的特征数量
    rfe.fit(X_train,y_train)
    target_columns = X_train.columns[rfe.support_.tolist()]
    return target_columns.tolist()

sklearn 还提供RFECV方法，该方法通过交查验证寻找最优的特征数量，这里说的交叉验证是不同列进行组合求平均，如果减少的特征会造成性能损失，将不去除任何特征。其思路是计算每个所有特征组合的误差，选择误差最小的特征子集

def rfecv_select(X_train,y_train):
    refcv = RFECV(estimator = RandomForestRegressor())
    refcv.fit(X_train,y_train)
    target_columns = X_train.columns[refcv.support_.tolist()]
    return target_columns.tolist()

该方法也存在一定缺陷：
（1）计算量大
（2）随着学习器的改变，最佳特征组合也会改变，因此适合在模型确定后在进行特征选择

参考链接：http://www.minxueyu.com/2020/03/29/RFE%E4%B8%8ERFECV%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0/

2.2 LVW（Las Vegas Wrapper）

LVW 是一个典型的包裹式特征选择方法，它在拉斯维加斯（Las Vegas method）框架下使用随机策略来进行子集搜索，并以最终分类器的误差为特征子集评价准则。

【算法】：

• 输入：数据集 D；特征集 A；学习算法 Σ；停止条件控制参数 T。
• 输出：特征子集 A*。
• 过程：

1. 初始化误差 E 为正无穷，d = |A|，A* = A，t = 0；
2. 进入循环，循环停止条件为 while t < T；
3. 随机产生特征子集 A’，设置 d’ = |A’|；
4. 选择特征子集对应部分的数据集 ，使用交叉验证法来估计学习器的误差。误差是特征子集 A’ 上的误差，若它比当前特征子集 A 上的误差更小，或误差相当但 A’ 中包含的特征数更少，则执行（a），否则执行（b）。
   （a）：t = 0，E = E’，d = d’，A* = A’；
   （b）：t = t + 1
5. 输出特征子集 A*。

【注意】：由于 LVW 算法中特征子集搜索采用了随机策略，而每次特征子集评价都需要训练学习器，计算开销很大，因此算法设置了停止条件控制参数 T。然而，整个 LVW 算法是基于拉斯维加斯方法框架，若初始特征数很多（即 |A| 很大）、T 设置较大，则算法可能运行很长时间都达不到停止条件。换言之，若有运行时间限制，则有可能给不出解。

3.嵌入式（embedding）

嵌入式特征选择是在训练的过程中自动进行了特征选择。

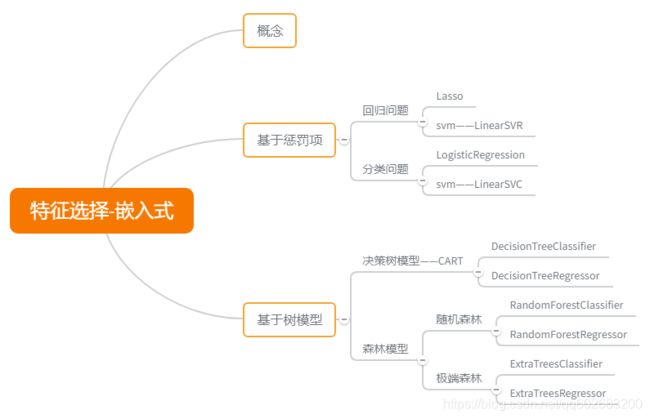
参考链接：https://clvsit.blog.csdn.net/article/details/90640595

3.1 基于惩罚项的特征选择法

Lasso回归

Lasso回归是用于缓解线性回归的过拟合问题的，优化的目标函数为平方误差加上系数的L1范数

相比于岭回归（使用L2范数），Lasso回归的优点是更易于获得稀疏解，从而达到特征选择的效果。
对w的推导过程如下：

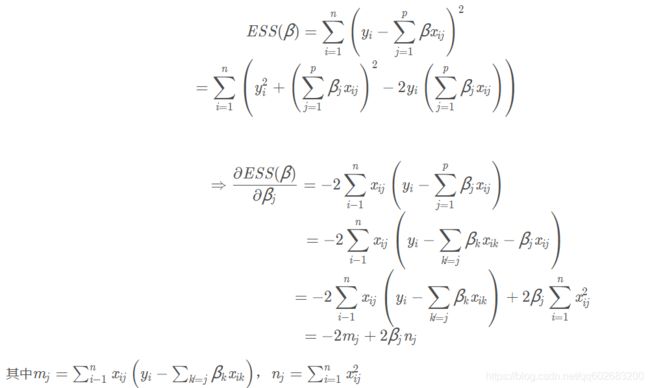
LassoCV(eps=0.001, n_alphas=100, alphas=None, fit_intercept=True, normalize=False, precompute=‘auto’, max_iter=1000, tol=0.0001, copy_X=True, cv=None, verbose=False, n_jobs=1, positive=False, random_state=None, selection=‘cyclic’)
• eps：指代 λ \lambda λ最小值与最大值的商，默认为0.001。
• n_alphas：指定 λ \lambda λ的个数，默认为100个。
• alphas：指定具体的 λ \lambda λ列表用于模型的运算。
• fit_intercept：bool类型，是否需要拟合截距项，默认为True。
• normalize：bool类型，建模时是否对数据集做标准化处理，默认为False。
• precompute：bool类型，是否在建模前计算Gram矩阵提升运算速度，默认为False。
• max_iter：指定模型的最大迭代次数。
• tol：指定模型收敛的阈值，默认为0.0001。
• copy_X：bool类型，是否复制自变量X的数值，默认为True。
• cv：指定交叉验证的重数。
• verbose：bool类型，是否返回模型运行的详细信息，默认为False。
• n_jobs：指定使用的CPU数量，默认为1，如果为-1表示所有CPU用于交叉验证的运算。
• positive：bool类型，是否将回归系数强制为正数，默认为False。
• random_state：指定随机生成器的种子。
• selection：指定每次迭代选择的回归系数，如果为’random’，表示每次迭代中将随机更新回归系数；如果为’cyclic’，则每次迭代时回归系数的更新都基于上一次运算。

Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=‘cyclic’)
• alphas：指定 λ \lambda λ值，默认为1。
• fit_intercept：bool类型，是否需要拟合截距项，默认为True。
• normalize：bool类型，建模时是否对数据集做标准化处理，默认为False。
• precompute：bool类型，是否在建模前计算Gram矩阵提升运算速度，默认为False。
• copy_X：bool类型，是否复制自变量X的数值，默认为True。
• max_iter：指定模型的最大迭代次数。
• tol：指定模型收敛的阈值，默认为0.0001。
• warm_start：bool类型，是否将前一次训练结果用作后一次的训练，默认为False。
• positive：bool类型，是否将回归系数强制为正数，默认为False。
• random_state：指定随机生成器的种子。
• selection：指定每次迭代选择的回归系数，如果为’random’，表示每次迭代中将随机更新回归系数；如果为’cyclic’，则每次迭代时回归系数的更新都基于上一次运算。

import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Lasso,LassoCV
from sklearn.metrics import mean_squared_error

data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
data=data.drop(['AGE','SEX'],axis=1)
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
                                                               test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数，使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=10,max_iter=10000)
lasso_cv.fit(x_train,y_train)

#基于最佳lambda值建模
lasso=Lasso(alpha=lasso_cv.alpha_,normalize=True,max_iter=10000)
lasso.fit(x_train,y_train)
#打印回归系数
print(pd.Series(index=['Intercept']+x_train.columns.tolist(),
                data=[lasso.intercept_]+lasso.coef_.tolist()))

#模型评估
lasso_pred=lasso.predict(x_test)
#均方误差
MSE=mean_squared_error(y_test,lasso_pred)
print(MSE)

参考链接：https://blog.csdn.net/weixin_43374551/article/details/83688913

3.2 基于树模型

树模型在构建的过程中实现了对特征的选择过程，下面写下树模型相关的内容。

3.2.1 决策树模型（CART 分类回归树）

决策树的构建主要分为3步：

• 特征选择
• 生成树
• 剪枝

3.2.1.1 DecisionTreeClassifier 分类树

1. 首先介绍一个重要的指标：基尼指数

特别的，对于二分类问题,如果第一类样本出现概率为p，则 Gini§ = 2p (1 - p)

• 基尼指数越大，样本不确定性越大；基尼指数越小，纯度越高
• 基尼指数用于衡量一个集合的纯度，即不确定性，Gini(D, A) 表示经过分割A分割后的不确定性
  
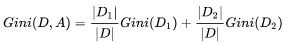
• CART分类树算法每次仅对某个特征的值进行二分

2. 构建流程
   

3.2.1.2 DecisionTreeRegressor 回归树

1. 决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，进行特征选择，生成二叉树。分枝时穷举每一个特征的每一个阈值，来寻找最优切分特征和最优切分点，衡量的方法是平方误差最小化。分枝直到达到预设的终止条件为止。

2. 生成过程
   

3. 优点：

• 简单直观，生成的决策树很直观。
• 基本不需要预处理，不需要提前归一化和处理缺失值。
• 使用决策树预测的代价是O(log2m)。m为样本数。
• 既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。
• 可以处理多维度输出的分类问题。
• 相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以很好解释。
• 可以交叉验证的剪枝来选择模型，从而提高泛化能力。
• 对于异常点的容错能力好，健壮性高。

4. 缺点：

• 决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
• 决策树会因为样本发生一点的改动，导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
• 寻找最优的决策树是一个NP难题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习的方法来改善。
• 有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。
• 如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。

参考链接1：总结分析
参考链接2：一目了然

3.2.2 森林模型

3.2.2.1 随机森林

随机森林是通过自助法（bootstrap）重采样技术, 从训练样本中有放回抽取k个样本生成新的训练样本集合，随机选择特征去分裂节点，生成k个分类树组成的随机森林，新数据的分类结果按分类树投票多少形成的分数而定。

优点：

• 随机森林不容易过拟合，且有较强抗噪能力
• 能够处理高为数据，不用单独做特征选择
• 既能处理离散数据，也能处理连续数据，数据集无需规范化
• 模型简单且解释性强
• 容易并行化

3.2.2.2 极端森林

ExtraTreesClassifier

用的少，用需要再更新。