李沐动手学深度学习V2-GRU门控循环单元以及代码实现

一. GRU门控循环单元

1. 介绍

我们可能会遇到这样的情况：
1）早期观测值对预测所有未来观测值具有非常重要的意义。 考虑一个极端情况，其中第一个观测值包含一个校验和， 目标是在序列的末尾辨别校验和是否正确。 在这种情况下，第一个词元的影响至关重要，我们希望有某些机制能够在一个记忆元里存储重要的早期信息， 如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度， 因为它会影响所有后续的观测值。
2) 一些词元没有相关的观测值。 例如在对网页内容进行情感分析时， 可能有一些辅助HTML代码与网页传达的情绪无关，希望有一些机制来跳过隐状态表示中的此类词元，对应于GRU中Z门。
3）序列的各个部分之间存在逻辑中断。 例如书的章节之间可能会有过渡存在， 或者证券的熊市和牛市之间可能会有过渡存在， 在这种情况下最好有一种方法来重置我们的内部状态表示，对应于GRU中R门。
因此GRU门控循环单元用来解决上面的情况。

2. 门控隐状态

门控循环单元与普通的循环神经网络之间的关键区别在于： 前者支持隐状态的门控，这意味着模型有专门的机制来确定应该何时更新隐状态， 以及应该何时重置隐状态，这些机制是可学习的，并且能够解决了上面列出的问题。 例如如果第一个词元非常重要，模型将学会在第一次观测之后不更新隐状态，同样模型也可以学会跳过不相关的临时观测，最后模型还将学会在需要的时候重置隐状态，下面详细讨论各类门控。

3.重置门和更新门

首先介绍重置门（reset gate）和更新门（update gate），把它们设计成$(0,1)$区间中的向量，这样就可以进行凸组合。重置门允许我们控制“可能还想记住”的过去状态的数量；更新门将允许我们控制新状态中有多少个是旧状态的副本。
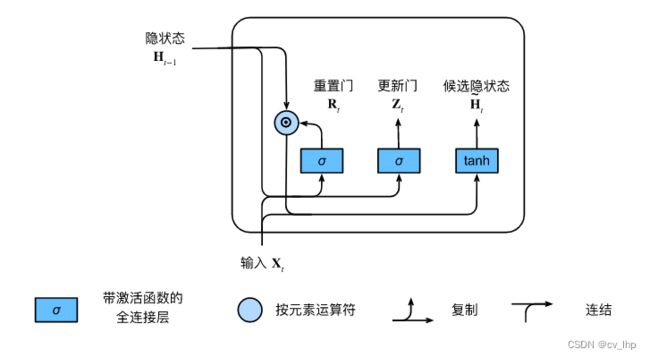
从构造这些门控开始，如下图所示描述了门控循环单元中的重置门和更新门的输入，输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

门控循环单元的数学表达：对于给定的时间步$t$，假设输入是一个小批量
${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$（样本个数：$n$，输入个数：$d$），上一个时间步的隐状态是${\mathbf{H}}_{t-1}\in {\mathbb{R}}^{n\times h}$（隐藏单元个数：$h$）。那么重置门${\mathbf{R}}_t\in {\mathbb{R}}^{n\times h}$和更新门${\mathbf{Z}}_t\in {\mathbb{R}}^{n\times h}$的计算如下所示：
$$\begin{array}{r}{\mathbf{R}}_t=\sigma ({\mathbf{X}}_t{\mathbf{W}}_{xr}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hr}+{\mathbf{b}}_r),\\ {\mathbf{Z}}_t=\sigma ({\mathbf{X}}_t{\mathbf{W}}_{xz}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hz}+{\mathbf{b}}_z),\end{array}$$
其中${\mathbf{W}}_{xr},{\mathbf{W}}_{xz}\in {\mathbb{R}}^{d\times h}$和${\mathbf{W}}_{hr},{\mathbf{W}}_{hz}\in {\mathbb{R}}^{h\times h}$是权重参数，${\mathbf{b}}_r,{\mathbf{b}}_z\in {\mathbb{R}}^{1\times h}$是偏置参数，注意在求和过程中会触发广播机制。使用sigmoid函数将输出值转换到区间$(0,1)$。

4. 候选隐状态

接下来将重置门${\mathbf{R}}_t$中的常规隐状态更新机制集成，得到在时间步$t$的候选隐状态（candidate hidden state）${\tilde{\mathbf{H}}}_t\in {\mathbb{R}}^{n\times h}$。
$${\tilde{\mathbf{H}}}_t=\tanh ({\mathbf{X}}_t{\mathbf{W}}_{xh}+\left({\mathbf{R}}_t\odot {\mathbf{H}}_{t-1}\right){\mathbf{W}}_{hh}+{\mathbf{b}}_h),$$
其中${\mathbf{W}}_{xh}\in {\mathbb{R}}^{d\times h}$和${\mathbf{W}}_{hh}\in {\mathbb{R}}^{h\times h}$是权重参数，${\mathbf{b}}_h\in {\mathbb{R}}^{1\times h}$是偏置项，符号$\odot$是Hadamard积（按元素乘积）运算符，同时使用tanh非线性激活函数来确保候选隐状态中的值保持在区间$(-1,1)$中。
与 RNN相比， GRU中的${\mathbf{R}}_t$和${\mathbf{H}}_{t-1}$的元素相乘可以减少以往状态的影响，也即是以往状态需要拿出多少来结合当前 ${\mathbf{X}}_t$从而更新 ${\tilde{\mathbf{H}}}_t$ 。每当重置门${\mathbf{R}}_t$中的项接近$1$时，也就相当于求RNN到当前时刻为止序列的隐状态。 对于重置门${\mathbf{R}}_t$中所有接近$0$的项，候选隐状态是以${\mathbf{X}}_t$作为输入的多层感知机的结果，如下图所示重置门的计算流程。

5. 隐状态

上述的计算结果只是候选隐状态，现在结合更新门${\mathbf{Z}}_t$的效果。这一步确定新的隐状态${\mathbf{H}}_t\in {\mathbb{R}}^{n\times h}$，在多大程度上来自旧的状态${\mathbf{H}}_{t-1}$（也即是不看当前时刻${\mathbf{X}}_t$的序列）和新的候选状态${\tilde{\mathbf{H}}}_t$。更新门${\mathbf{Z}}_t$和$1-{\mathbf{Z}}_t$仅需要在${\mathbf{H}}_{t-1}$和${\tilde{\mathbf{H}}}_t$之间进行按元素的凸组合就可以实现这个目标。这就得出了门控循环单元隐状态最终更新公式（处于旧的状态${\mathbf{H}}_{t-1}$（也即是不看当前时刻${\mathbf{X}}_t$的序列）和新的候选状态${\tilde{\mathbf{H}}}_t$（看当前时刻${\mathbf{X}}_t$的序列）之间，取决于${\mathbf{Z}}_t$有多大）：
$${\mathbf{H}}_t={\mathbf{Z}}_t\odot {\mathbf{H}}_{t-1}+(1-{\mathbf{Z}}_t)\odot {\tilde{\mathbf{H}}}_t.$$
每当更新门${\mathbf{Z}}_t$接近$1$时，模型就倾向只保留旧状态，此时来自${\mathbf{X}}_t$的信息基本上被忽略，从而有效地跳过了依赖链条中的时间步$t$。相反当${\mathbf{Z}}_t$接近$0$时，新的隐状态${\mathbf{H}}_t$就会接近候选隐状态${\tilde{\mathbf{H}}}_t$。
这些设计可以帮助我们处理循环神经网络中的梯度消失问题（因为${\mathbf{H}}_t由{\mathbf{H}}_{t-1}和{\tilde{\mathbf{H}}}_t$相加组成的，而不是RNN中每次对隐状态进行更新覆盖而成），并更好地捕获时间步距离很长的序列的依赖关系。例如如果整个子序列的所有时间步的更新门都接近于$1$，则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束，也即是当前时间步的隐状态和序列起始时间步的旧隐状态相同，隐状态在这个过程中没有改变， 更新门计算流如下图所示。

总之，门控循环单元具有以下两个显著特征：

• 重置门有助于捕获序列中的短期依赖关系。
• 更新门有助于捕获序列中的长期依赖关系。

二. 从零实现GRU

1. 数据集读取

读取时间机器数据集：

import torch
import d2l.torch
from torch import nn
batch_size,num_steps = 32,35
train_iter,vocab = d2l.torch.load_data_time_machine(batch_size,num_steps)

2. 模型参数初始化

接着初始化模型参数：从标准差为 0.01 的高斯分布中初始化权重， 并将偏置项设为 0 ，超参数num_hiddens定义隐藏单元的数量， 实例化与更新门、重置门、候选隐状态和输出层相关的所有权重和偏置。

def get_params(vocab_size,num_hiddens,device):
    input_size = output_size = vocab_size
    def normal(shape):
        return torch.randn(size=shape,device=device)*0.01
    def three():
        return (normal(shape=(input_size,num_hiddens)),
                normal(shape=(num_hiddens,num_hiddens)),
                torch.zeros(num_hiddens,device=device))
    W_xr,W_hr,b_r = three()  # 更新门参数
    W_xz,W_hz,b_z = three()  # 重置门参数
    W_xh,W_hh,b_h = three()  # 候选隐状态参数
    # 输出层参数
    W_hq = normal(shape=(num_hiddens,output_size))
    b_q = torch.zeros(output_size,device=device)
    # 设置参数梯度为True
    params = [W_xr,W_hr,b_r,W_xz,W_hz,b_z,W_xh,W_hh,b_h,W_hq,b_q]
    for param in params:
        param.requires_grad_(True)
    return params

3. 定义模型

定义隐状态的初始化函数init_gru_state()：此函数返回一个形状为（批量大小，隐藏单元个数）的张量，张量的值全部为零。

def init_gru_state(batch_size,num_hiddens,device):
    return (torch.zeros(size=(batch_size,num_hiddens),device=device),)

定义门控循环单元模型：模型的架构与基本的循环神经网络单元是相同的， 只是权重更新公式更为复杂。

def gru(inputs,state,params):
    W_xr,W_hr,b_r,W_xz,W_hz,b_z,W_xh,W_hh,b_h,W_hq,b_q = params
    H, = state
    outputs = []
    for X in inputs:
        R = torch.sigmoid((X @ W_xr)+(H @ W_hr)+b_r)
        Z = torch.sigmoid((X @ W_xz)+(H @ W_hz)+b_z)
        H_tilda = torch.tanh((X @ W_xh)+((R*H) @ W_hh)+b_h)
        H = Z*H+(1-Z)*H_tilda
        Y = H @ W_hq+b_q
        outputs.append(Y)
    return torch.cat(outputs,dim=0),(H,)

4. 训练与预测

训练和预测的工作方式：训练结束后打印每轮训练的困惑度， 以及前缀“time traveler”和“traveler”的预测序列。

vocab_size,num_hiddens,device = len(vocab),256,d2l.torch.try_gpu()
num_epochs,lr = 500,1
model = d2l.torch.RNNModelScratch(vocab_size,num_hiddens,device,get_params,init_gru_state,gru)
d2l.torch.train_ch8(model,train_iter,vocab,lr,num_epochs,device,use_random_iter=False)

5. 从零实现GRU全部代码

import torch
import d2l.torch
from torch import nn

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.torch.load_data_time_machine(batch_size, num_steps)


def get_params(vocab_size, num_hiddens, device):
    input_size = output_size = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01

    def three():
        return (normal(shape=(input_size, num_hiddens)),
                normal(shape=(num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xr, W_hr, b_r = three()  # 更新门参数
    W_xz, W_hz, b_z = three()  # 重置门参数
    W_xh, W_hh, b_h = three()  # 候选隐状态参数
    # 输出层参数
    W_hq = normal(shape=(num_hiddens, output_size))
    b_q = torch.zeros(output_size, device=device)
    # 设置参数梯度为True
    params = [W_xr, W_hr, b_r, W_xz, W_hz, b_z, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params


def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros(size=(batch_size, num_hiddens), device=device),)


def gru(inputs, state, params):
    W_xr, W_hr, b_r, W_xz, W_hz, b_z, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)


vocab_size, num_hiddens, device = len(vocab), 256, d2l.torch.try_gpu()
num_epochs, lr = 500, 1
model = d2l.torch.RNNModelScratch(vocab_size, num_hiddens, device, get_params, init_gru_state, gru)
d2l.torch.train_ch8(model, train_iter, vocab, lr, num_epochs, device, use_random_iter=False)

三. 使用Pytorch框架实现GRU

1. 使用Pytorch框架训练和预测

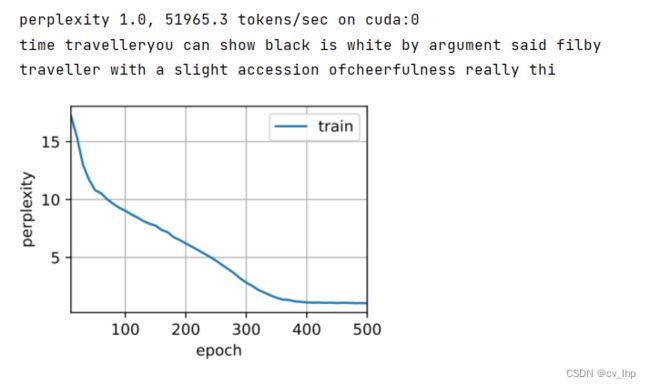
高级API包含了前文介绍的所有配置细节， 所以可以直接实例化门控循环单元模型。 这段代码的运行速度要快得多， 因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节，训练结果和预测结果如下图所示。

inputs_size = vocab_size
gru_layer = nn.GRU(inputs_size,num_hiddens)
model = d2l.torch.RNNModel(gru_layer,len(vocab))
model = model.to(device)
d2l.torch.train_ch8(model,train_iter,vocab,lr,num_epochs,device,use_random_iter=False)

2. 使用Pytorch框架实现GRU全部代码

inputs_size = vocab_size
gru_layer = nn.GRU(inputs_size,num_hiddens)
model = d2l.torch.RNNModel(gru_layer,len(vocab))
model = model.to(device)
d2l.torch.train_ch8(model,train_iter,vocab,lr,num_epochs,device,use_random_iter=False)

四. 小结

• 门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系。
• 重置门R有助于捕获序列中的短期依赖关系。
• 更新门Z有助于捕获序列中的长期依赖关系。
• 重置门R打开时，门控循环单元包含基本循环神经网络；更新门Z打开时，门控循环单元可以跳过当前时间步的子序列。

五. 链接

循环神经网络RNN第一篇：李沐动手学深度学习V2-NLP序列模型和代码实现
循环神经网络RNN第二篇：李沐动手学深度学习V2-NLP文本预处理和代码实现
循环神经网络RNN第三篇：李沐动手学深度学习V2-NLP语言模型、数据集加载和数据迭代器实现以及代码实现
循环神经网络RNN第四篇：李沐动手学深度学习V2-RNN原理
循环神经网络RNN第五篇：李沐动手学深度学习V2-RNN循环神经网络从零实现
循环神经网络RNN第六篇：李沐动手学深度学习V2-使用Pytorch框架实现RNN循环神经网络
循环神经网络GRU第七篇：李沐动手学深度学习V2-GRU门控循环单元以及代码实现
循环神经网络LSTM第八篇：李沐动手学深度学习V2-LSTM长短期记忆网络以及代码实现
深度循环神经网络第九篇：李沐动手学深度学习V2-深度循环神经网络和代码实现
双向循环神经网络第十篇：李沐动手学深度学习V2-双向循环神经网络Bidirectional RNN和代码实现