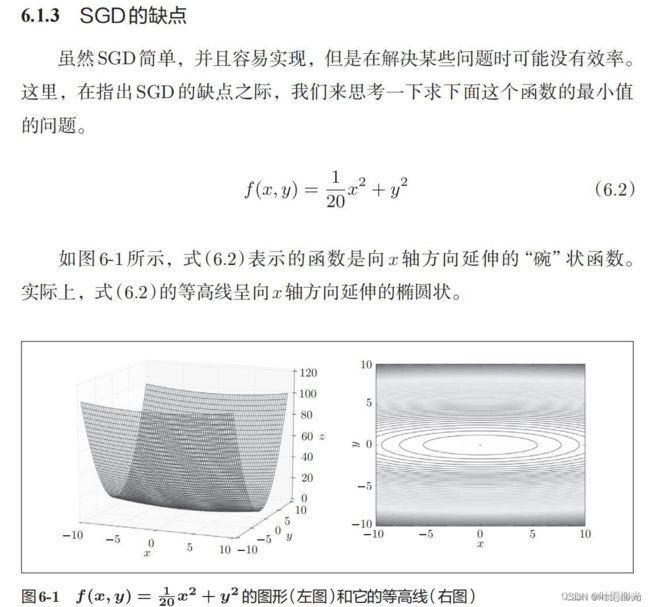
NNDL 作业11：优化算法比较

1. 编程实现下式，并观察特征

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
 
def func(x, y):
    return x * x / 20 + y * y
 
 
def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数
 
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
 
paint_loss_func()

2. 观察梯度方向

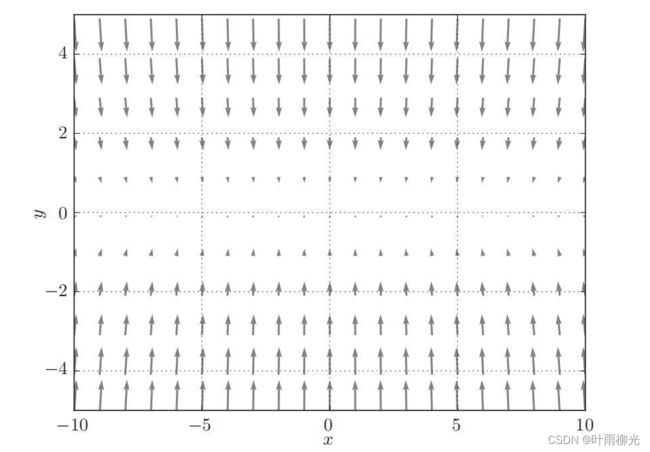
Y轴方向梯度大，X轴方向梯度小；很多位置的梯度并没有指向最小位置(0,0)

3. 编写代码实现算法，并可视化轨迹

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
 
 
class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
 
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
 
 
class Momentum:
    """Momentum SGD"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]
 
 
class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
 
 
class AdaGrad:
    """AdaGrad"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class RMSprop:
    """RMSprop"""
 
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
 
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
 
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
 
        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
 
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
 
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
 
 
def f(x, y):
    return x ** 2 / 20.0 + y ** 2
 
 
def df(x, y):
    return x / 10.0, 2.0 * y
 
 
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
 
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
 
idx = 1
 
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
 
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
 
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
 
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
 
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0
 
    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
 
plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

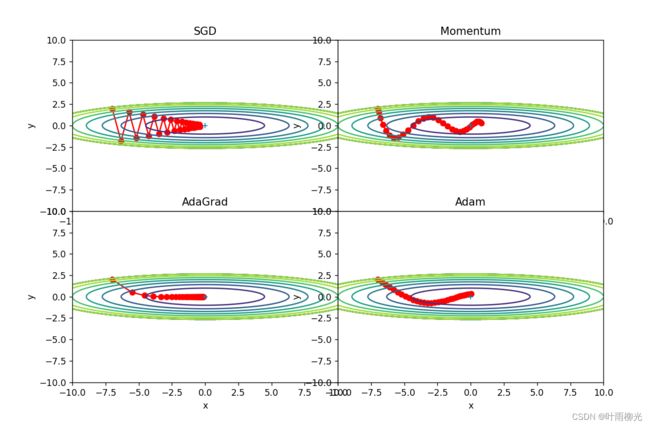
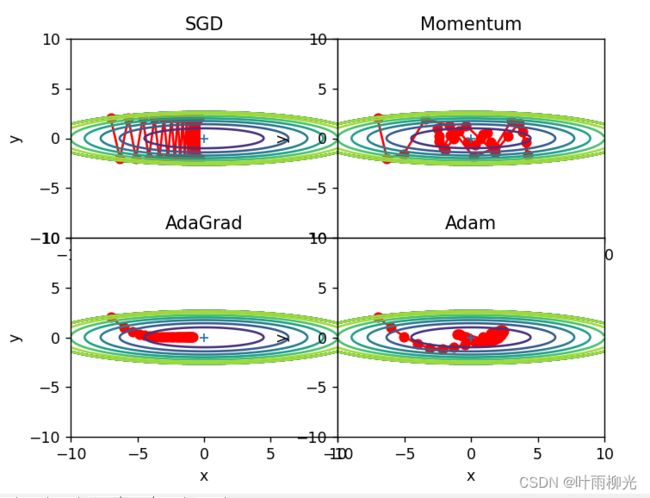
从可视化结果来看，收敛效果排序依次为AdaGrad、Adam、Momentum、SGD。

4. 分析上图，说明原理

1.为什么SGD会走“之字形”？其它算法为什么会比较平滑？

因为梯度的方向并没有指向最小值的方向，SGD只是单纯的朝着梯度方向移动，可能会“走过了”，再继续向梯度方向走，其他算法平滑原因：因为y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之”字形的变动程度有所衰减。

2.Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

Momentum借助了物理中的动量的概念，即前几次的梯度也会参与计算。为了表示动量，引入一个新的变量V，V是之前的梯度的累加，但是在每个回合都会有一定的衰减。它的特点是当前后梯度方向不一致时，能够加速学习，前后梯度方向一致时，能够抑制震荡。这样可以减缓之字形抖动。
对于梯度大的参数设置小的步长，对于梯度小的参数，设置大的步长。类比于在缓坡上面，我们可以大步长的前进，在陡坡上面，这需要小步长的前进。adagrad则是参考了这个思路。体现在图上为:函数的取值高效地向着最小值移动。

3.仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？

是，从图中可以看到在相同的点数（迭代次数）后，AdaGrad更接近收敛的位置，说明AdaGrad的效率更高而且不容易波动。

4.四种方法分别用了多长时间？是否符合预期？

符合预期，这四种方法参数计算的复杂程度逐渐增加，所以与之对应的计算时间就会增加。

5.调整学习率、动量等超参数，轨迹有哪些变化？

学习率=0.1

lr=0.5
lr=1

lr=3

可以看出，在学习率较低时SGD和Momentum效率较高，但是准确率低，学习率较高时Ada和AdaGrad收敛效果更好，其中AdaGrad效果最好。

5. 总结SGD、Momentum、AdaGrad、Adam的优缺点

随机梯度下降（stochastic gradient descent）方法，指的是在迭代的每次过程中，我们随机均匀采样的一个样本索引$i\in 1,...,ni\in \left\{1,...,n\right\}i\in 1,...,n$，并计算梯度∇f 来迭代x。可以看到，每次迭代的计算开销从梯度下降的O(n)降到了常数O(1)。
优点：训练速度快，对于很大的数据集，也能以较快的速度进行收敛。
缺点：对于参数比较敏感，需要注意参数的初始化；由于是抽取的批量数据，因此得到的梯度不可避免有误差。学习速率需要逐渐减小，否则模型会无法收敛。模型在每一次的iteration中受抽样的影响比较大，也就是说梯度含有较大的噪声，不能很好地反应真实梯度。
Momentum
上面的SGD的问题在于每次迭代计算时，梯度含有较大的噪音。而Momentum可以比较好的缓解这个问题。尤其是在面对小而连续的梯度，但是含有很多噪音时，可以很好的加速学习。Momentum借用了物理中的动量概念，即前一次的梯度也会参与运算。为了表示动量，引入了一个新的变量v(velosity)。v是之前的梯度的累加，但是每次更新参数时会有一定的衰减。
AdaGrad
优点：
适合处理稀疏梯度，能实现学习率的自动更改。如果这次梯度大，那么学习速率衰减的就快一些。如果这次梯度小，那么学习速率就衰减的慢一些。
缺点：
(1) 仍依赖于人工设置一个全局学习率
(2)中后期，分母上梯度平方的累加会越来越大，步长也越来越小，使gradient接近0，使得训练提前结束。我们通常不倾向于使用AdaGrad对神经网络做训练。
Adam
优点：对内存需求较小，为不同的参数计算不同的自适应学习率
缺点：可能不收敛；可能错过全局最优解.
参考：SGD、Momentum、 AdaGrad、Adam
通俗解读SGD、Momentum、Nestero Momentum、AdaGrad、RMSProp、Adam优化算法

6. Adam这么好，SGD是不是就用不到了？（选做）

这里有网上的参考：Adam那么棒，为什么还对SGD念念不忘 (2)—— Adam的两宗罪
Adam那么棒，为什么还对SGD念念不忘


Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

文章告诉我们Adam也有其缺点，具体用那个算法还要根据数据的情况具体选择。
这里还有文章中改进的一种方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错

总结：

这次的作业完成起来比较简单，但是不能为完成作业而完成，要理解各个算法的优缺点，以后才可能真正应用到。