机器学习的分类、回归、聚类问题

分类、回归问题都是监督学习，本质都是对输入做出预测，都要建立映射关系。分类问题输出的是物体所属的类别（瓜是好瓜吗），回归问题输出的是数值（瓜会卖到多少钱）。聚类是无监督学习

一.分类问题

分类问题输出的是物体所属的类别，即输出结果是：“好瓜/坏瓜”、“晴天/阴天/雨天”...，分类问题输出的值是定性的，目的是为了寻找决策边界。单一的分类方法主要包括：决策树、贝叶斯、人工神经网络、K-近邻、支持向量机和基于关联规则的分类等；另还有组合单一方法的集成学习算法，如Bagging、Boosting等。

1.决策树

通过对历史数据进行测算，实现对新数据进行分类和预测。例如，我们要对“这是好瓜吗？”进行决策，就要进行一系列的判断或”子决策“：先看“是什么颜色”，再“根蒂是什么形态”，再判断“敲起来是什么声音”，最后得出决策：这是个好瓜/坏瓜。

 一般的，一棵决策树包括一个根节点、若干个内部节点（根蒂、敲声、色泽）和若干个叶节点（好/坏瓜）。其中，叶节点对应决策结果，其他每个节点对应一个属性测试；每个节点包含的样本集合根据属性测试的结果被划分至子节点中；根节点包含样本全集，子节点样本集数量逐渐减少；根节点到每个叶结点的路径对应了一个判定测试序列。其基本流程遵循“分而治之”策略，其生成是一个递归过程。

关于决策树算法详细介绍可参考文章：

决策树分类和预测算法的原理及实现_czp11210的博客-CSDN博客_预测算法

2.贝叶斯

利用概率统计知识进行分类，主要利用Bayes定理来预测一个未知类别的样本属于某个类别的可能性，并选择其中可能性最大的一个类别作为该样本的最终类别。由于贝叶斯定理的成立本身需要一个很强的条件独立性假设前提，而此假设在实际情况中经常是不成立的，因而其分类准确性就会下降。为此就出现了许多降低独立性假设的贝叶斯分类算法，如TAN（Tree Augmented Na?ve Bayes)算法，它是在贝叶斯网络结构的基础上增加属性对之间的关联来实现的。 

3.人工神经网络

神经网络通常需要进行训练，训练的过程就是网络进行学习的过程。训练改变了网络节点的连接权的值使其具有分类的功能，经过训练的网络就可用于对象的识别。  

4.K-近邻（kNN）

基于实例的分类方法，找出与未知样本X距离最近的K个训练样本，看这k个样本中多数属于哪一类，就把x归于那一类。k-近邻方法是一种懒惰学习方法，它存放样本，直到需要分类时才进行分类，如果样本集比较复杂，可能会导致很大的计算开销，因此无法应用到实时性很强的场合。  

5.支持向量机

最大特点是根据结构风险最小化准则，以最大化分类间隔构造最优分类超平面来提高学习机的泛化能力，较好地解决了非线性、高维数、局部极小点等问题。对于分类问题，支持向量机算法根据区域中的样本计算该区域的决策曲面，由此确定该区域中未知样本的类别。

6.基于关联规则的分类

关联分类方法一般由两步组成：第一步用关联规则挖掘算法从训练数据集中挖掘出所有满足指定支持度和置信度的类关联规则；第二步使用启发式方法从挖掘出的类关联规则中挑选出一组高质量的规则用于分类。属于关联分类的算法主要包括CBA，ADT ，CMAR 等。

7.集成学习

实际应用的复杂性和数据的多样性往往使得单一的分类方法不够有效。因此，学者们对多种分类方法的融合即集成学习进行了广泛的研究。它试图通过连续调用单个的学习算法，获得不同的基学习器，然后根据规则组合这些学习器来解决同一个问题，可以显著的提高学习系统的泛化能力。

二.回归问题

对数值型连续随机变量进行预测和建模。

回归问题输出的物体的值，温度是多少度，房价是多少万...，回归问题输出的值是定量的，目的是为了寻找最优拟合，对真实值的一种逼近预测，当预测值与真实值相近、误差较小时，认为是一个好的回归。下面介绍几种最基本的回归方法。

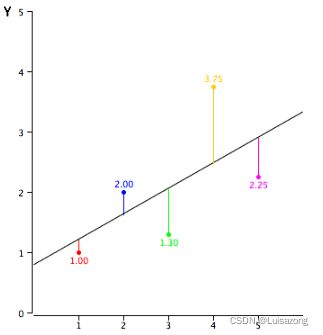
1.线性回归

线性回归常被用于线性预测模型，此模型中，因变量是连续的，自变量可连续可离散，回归线的性质是线性的。

1.1一元线性回归

一元线性回归是评估一个自变量和一个因变量之间的关系，它是被方程式：Y = a + b*X + e 所表示，这里 a 为截距，b 为斜率和，e 为误差项。

 1.2多元线性回归

多元回归评估多个自变量与一个因变量之间的关系，因变量和自变量之间是线性关系，可表明多个独立变量对因变量影响的强度。

 

1.3多元多重回归分析

讨论多个自变量与多个因变量的线性依赖关系。

2.多项式回归

当自变量的幂次大于1，则不是线性回归，是多项式回归，回归方程是多项式回归方程，最佳拟合线不是直线，是一条拟合数据点的曲线。

 问题：

可能存在用较高次多项式去拟合较低次多项式的情况，进而导致过拟合。

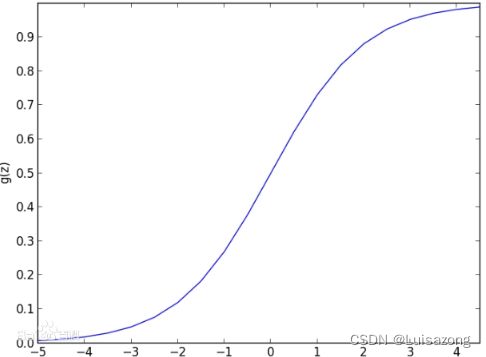
3.逻辑回归

逻辑回归是一种广义线性回归，与多线元性回归的模型形式基本相同，多元线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而逻辑回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。它不要求自变量和因变量是线性关系，可以处理各种类型的关系，因为它对预测的相对风险指数OR使用了一个非线性的log转换。可以用于医学方面1）寻找危险元素：寻找某一疾病的危险因素；2）预测：根据逻辑回归模型预测发生某情况的概率有多大；3）判别：判别某人属于某病的概率有多大。

 

三.聚类问题

聚类的思维方式可通俗表达为：把认知为相似的事物放到一起作为一类，比如我们去参观一个画展，我们完全对艺术一无所知，但是欣赏完多幅作品之后，我们也能把它们分成不同的派别（比如哪些更朦胧一点，哪些更写实一些，即使我们不知道什么叫做朦胧派，什么叫做写实派，但是至少我们能把他们分为两个类）。

常见的聚类算法可参考文章：

常见的六大聚类算法_从未完美过的博客-CSDN博客_聚类算法