模拟退火算法求解旅行商问题

模拟退火算法求解旅行商问题

---

旅行商（TSP）问题

由威廉哈密顿爵士和英国数学家克克曼T.P.Kirkman于19世纪初提出。问题描述如下：
有若干个城市，任何两个城市之间的距离都是确定的，现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次，最后回到出发的城市，问如何事先确定一条最短的线路已保证其旅行的费用最少？

---

一、TSP问题分析

旅行商问题是一个NP完全问题，目前求解TSP问题的主要方法有模拟退火算法、遗传算法、启发式搜索法、Hopfield神经网络法、蚁群算法等。其中模拟退火算法时局部搜素算法的扩展，理论上来说，它是一个全局最优算法，用来在一个大的搜寻空间内找寻命题的最优解。

二、模拟退火算法

1.一秒理解算法

模拟退火算法起源于物理上存在的固体退火原理。

物理退火：在一个材料加热后，经过一定的速率冷却，最后趋于稳定。
在材料加热后，分子热运动也会随之增大，即内部粒子会处于无序态，在随着温度逐渐的减小，粒子的运动也会越来越缓慢，位置也会逐渐的趋于有序，最后当温度达到平衡态时，粒子也会处于平衡态，此时，该材料会处于一个稳定且以最低内能存在。

模拟退火：它的原理与物理退火类似。模拟退火算法从一个比较高的温度开始，随着温度参数的下降，会有概率跳出当前已找到的局部最优解，随机寻找目标函数的全局最优解。

模拟退火算法其实是一种贪心算法，但是并不是完全的贪心算法，因为它会有概率跳出当前最优解。
对于模拟退火算法的解释，可以参考另一种算法：爬山算法。
爬山算法是一种纯粹的贪心算法，这种算法每次都会从目前解的附近找一个最优解来作为下一次的解，一直趋于稳定，即找到了该算法所认为的最优解。但是这种算法有一个巨大的缺陷，就是很容易陷入局部最优解，却不是整个问题的最优解。
该算法搜索到A点时，它就以为自己找到了最优解，便不会不去接受其他任何比它大的解了，也就无法跨国坡顶C，到达真正的最优解B。

模拟退火算法更像是一个爬山算法的改进，在该算法陷入局部最优解时，会有一定的概率跳出该局部最优解，转去搜索其他最优解，即该算法可以接受一个比当前解更差的解，进而趋于稳定后，达到一个全局的最优解。（具体见算法原理）

2.算法原理

可以这么理解，模拟退火算法是一个改进型的贪心算法。它的原理也是基于贪心算法来进行的，在算法中，首先需要对一个最短路程进行搜索，如果找到了一个比当前解更优的解，会直接用此路程当作最短路程；但是如果找到一个比当前解更差的解，会以一定的概率来接受这个差解，因此有可能会跳出所提到的局部最优解，进而到达全局的最优解。如下图所示，当前位置若处于A点，如果搜索到了C点，则存在一定的概率会接受C，进而再一次进行搜索，达到B，即全局最优解。

在讲模拟退火算法时，一直在提这个概率的问题，下面就让我们来分析一下这个概率到底是如何得到。
其实这个概率同样参考了物理退火的过程。
根据Metropolis准则，在温度为T时，粒子趋于平衡的概率为P(dE) = exp( dE/(kT) )

其中的k为常识，exp为自然指数，由于是降火，则dE<0，则dE/kT<0，则exp(dE/kT)取值是(0,1)，即P(dE)的函数取值范围是（0,1）。

该公式可以理解成：
随着温度从高到低，能量差dE的概率也就会来越小，直到最后能量差的概率很小。
应用到我们算法中后，就体现成：
刚开始温度很高的时候，搜索过程会非常的灵活，会有很大的概率跳出局部的最优解，随着温度降低，这个概率会越来越小，最后趋于稳定。
我们采用P(dE)来决定是否接受这次移动，将我们的目标函数值当成内能，将控制的循环参数当成温度T，通过逐渐的衰减参数，直到得到最优解。

在每次的循环求解中：
（1）若下一次解为更优解，则接受下一次解；
（2）若下一次解比当前解要差，则以一定的概率接受移动，这个概率随着时间逐渐降低，如果全局最优解距离当前解不太远，很有可能到达最优解，这将会通过我们设置的衰减参数来决定。

我们提到了衰减系数这一值，这要由我们自己设定，决定每次温度需要衰减的幅度，一般为[0.8,1)，衰减系数越大，温度降低的越慢，更容易查找到全局最优解，但是相对的，时间也会耗费的更多；衰减系数越小，温度降低的越快，算法结束的也就越快，可能最后无法找到我们想得到的全局最优解，因此要合理设置。

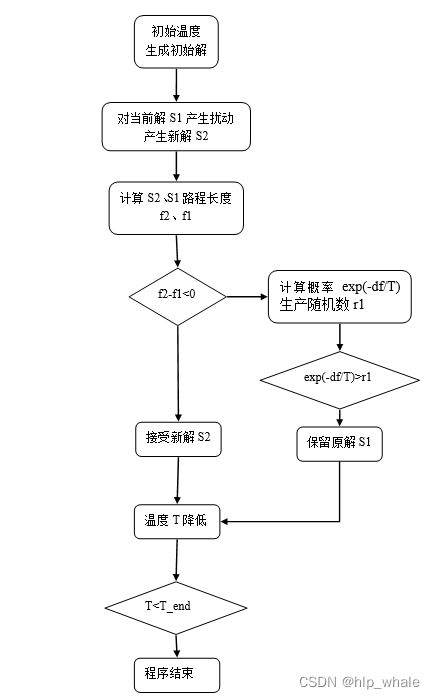
3. 算法流程

（1）初始化温度T0,令当前的温度为T=T0，,产生一个初始的随机解S1
（2）对当前的解S1进行随机的扰动，产生一个新解S2
（3）计算S2的路径长度f2，和S1的路径长度f1
（4）若f2-f1<0，则接受S2作为新解；若f2>=f1，则计算是否接受S2的概率exp(-df/T)，产生一个在（0,1）的随机数r1，如果exp(-df/T)>r1，则接受S2作为新解；否则保留当前解S1。
（5）温度降低，具体体现在当前温度乘以温度降低系数，如果降低后的温度低于设置的最低值，则终止算法，程序结束；否则返回步骤（2）。

三、伪代码

	/*其中
	T为当前温度
	T_end为设置最小温度
	s2为创建的新路径
	s1为当前的路径
	df为路径差
	r为衰减系数*/
	while(T > T_end)//当前温度是否大于设置的温度最小值
{
	create(s2);//创造新的路径
	df = f(s2) - f(s1);//得到两个路径的差
	if (df < 0)//新创造的路径更短
	{
		s1 = s2;//采用新路径
	}
	else
	{
		if (exp(df / T) > random(0, 1))//是否采用更差的路径
			s1 = s2;
	}
	T = T * r;//温度衰减，r为衰减系数 0
}

这就是算法实现的核心思路。

四、运行结果

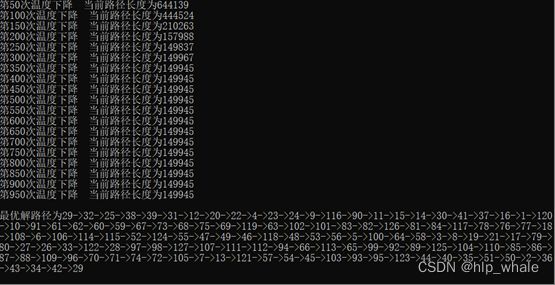
我所采用了128项数据（保存在文件中），文末可取。

以下为运行结果：

可以看出，刚开始的路径长度为644139，随着温度不断下降，路径长度也在不断的更新。其中第250次温度下降时路径长度为149837，第300次温度下降时路径长度为149967，可以看出路径长度变大，此处就可以体现出该算法中以一定概率接受差解的思想。
但是算法找到的最终解不一定是最优解，如下图。

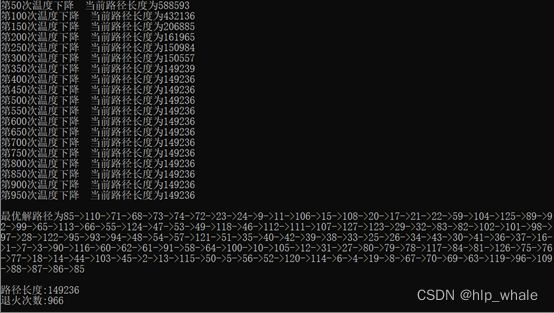
这次运行结果为149236，更低于上次运行得到的最短路径149945，由此可得到，该模拟退火算法最终结果不一定为最优解，而是较优解。

五、代码（C++）

#include 
#include 
#include
#include
using namespace std;

//采用类将退火模拟算法封装
//使用者可以传入数组坐标来使用退火模拟算法
class SAA {
public:
    //初始化
    SAA(double s[][2], int s_l)//传入参数二维数组和长度
    {
        //初始化add二维数组
        for (int i = 0; i < s_l; i++)
        { 
            vector<double> t;
            for (int j = 0; j < 2; j++)
            {              
                t.push_back(s[i][j]);
            }
            add.push_back(t);
        }
        goat.resize(s_l);//赋值数组长度
        last.resize(s_l);
        n = s_l;//赋值位置个数
        for (int i = 0; i < n; i++)//先对当前解初始化
        {
            goat[i] = i + 1;
        }
    }
    //计算两点距离
    double dis(vector<double> a, vector<double> b)//传入两个坐标
    {
        return sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]));
    }
    //计算路径长度
    double path_l(vector<int> pa)//传入路径数组
    {
        double path = 0;
        for (int i = 0; i < n - 1; i++)
        {
            path += dis(add[pa[i] - 1], add[pa[i + 1] - 1]);
        }
        path += dis(add[pa[0] - 1], add[pa[n - 1] - 1]);//从最后一个返回第一个
        return path;
    }
    //随机改变新的解
    void change()
    {
        double e1 = ((double)rand()) / (RAND_MAX + 1.0);
        double e2 = ((double)rand()) / (RAND_MAX + 1.0);
        int p1 = (int)(n * e1);//产生两个地点
        int p2 = (int)(n * e2);
        int t = goat[p1];
        goat[p1] = goat[p2];
        goat[p2] = t;
    }
    //模拟退火核心
    void Tsp()
    {
        double path1;//路径1
        double path2;//路径2
        double pathcut;//路径差
        T = T_start;
        srand((unsigned)time(NULL));//设置随机种子

        while (T > T_end)//温度低于最低时跳出循环
        {
            for (int i = 0; i < l; i++)
            {
                last.assign(goat.begin(), goat.end());//复制
                change();//新解
                //计算路径差
                path1 = path_l(last);
                path2 = path_l(goat);
                pathcut = path2 - path1;
                //退火准则
                if (pathcut >= 0)
                {
                    r = ((double)rand()) / (RAND_MAX);//0-1的数
                    if (exp(-pathcut / T) <= r)//是否接受新解
                    {
                        goat.assign(last.begin(), last.end());//接受
                    }
                }
            }
            sum++;//计数器
            if(sum % 50==0)
                cout <<"第" << sum << "次温度下降  当前路径长度为" << path_l(goat) << endl;
            T *= p;//降温
        }
    }
    //路径打印
    void path_print()
    {
        cout << endl;
        cout << "最优解路径为";
        for (int i = 0; i <= n-1; i++)
        {
            cout << goat[i] << "->";
        }
        cout << goat[0] << endl;
        cout << endl;
        cout << "路径长度:" << path_l(goat) << endl;
        cout << "退火次数:" << sum << endl;
    }
private:
    vector<vector<double>> add;//坐标
    vector<int> goat;//存放当前解
    vector<int> last;//存放上一个解
    double p=0.97;//退火系数
    int l = 1000;//每个温度时的迭代系数
    int n;//位置个数
    
    double T_end = 1e-8;//结束温度
    double T_start = 60000;//初始温度
    double T;//当前温度
    double r;//0-1的随机数决定是否接受新解
    int  sum=0;//记录降温次数
};
int main()
{
    double s[127][2];
    ifstream infile("data.txt");
    string buf1;
    string buf2;
    string buf3;
    int i = 0;
    while (!infile.eof())
    {
        infile >> buf1;
        infile >> buf2;
        infile >> buf3;
        s[i][0] = stod(buf2);
        s[i][1] = stod(buf3);
        i++;
    }
    SAA tsp(s, 127);//创建旅行商
    tsp.Tsp();//进行退火模拟
    tsp.path_print();//打印结果
}

数据

   1   9860  14152
   2   9396  14616
   3  11252  14848
   4  11020  13456
   5   9512  15776
   6  10788  13804
   7  10208  14384
   8  11600  13456
   9  11252  14036
  10  10672  15080
  11  11136  14152
  12   9860  13108
  13  10092  14964
  14   9512  13340
  15  10556  13688
  16   9628  14036
  17  10904  13108
  18  11368  12644
  19  11252  13340
  20  10672  13340
  21  11020  13108
  22  11020  13340
  23  11136  13572
  24  11020  13688
  25   8468  11136
  26   8932  12064
  27   9512  12412
  28   7772  11020
  29   8352  10672
  30   9164  12876
  31   9744  12528
  32   8352  10324
  33   8236  11020
  34   8468  12876
  35   8700  14036
  36   8932  13688
  37   9048  13804
  38   8468  12296
  39   8352  12644
  40   8236  13572
  41   9164  13340
  42   8004  12760
  43   8584  13108
  44   7772  14732
  45   7540  15080
  46   7424  17516
  47   8352  17052
  48   7540  16820
  49   7888  17168
  50   9744  15196
  51   9164  14964
  52   9744  16240
  53   7888  16936
  54   8236  15428
  55   9512  17400
  56   9164  16008
  57   8700  15312
  58  11716  16008
  59  12992  14964
  60  12412  14964
  61  12296  15312
  62  12528  15196
  63  15312   6612
  64  11716  16124
  65  11600  19720
  66  10324  17516
  67  12412  13340
  68  12876  12180
  69  13688  10904
  70  13688  11716
  71  13688  12528
  72  11484  13224
  73  12296  12760
  74  12064  12528
  75  12644  10556
  76  11832  11252
  77  11368  12296
  78  11136  11020
  79  10556  11948
  80  10324  11716
  81  11484   9512
  82  11484   7540
  83  11020   7424
  84  11484   9744
  85  16936  12180
  86  17052  12064
  87  16936  11832
  88  17052  11600
  89  13804  18792
  90  12064  14964
  91  12180  15544
  92  14152  18908
  93   5104  14616
  94   6496  17168
  95   5684  13224
  96  15660  10788
  97   5336  10324
  98    812   6264
  99  14384  20184
 100  11252  15776
 101   9744   3132
 102  10904   3480
 103   7308  14848
 104  16472  16472
 105  10440  14036
 106  10672  13804
 107   1160  18560
 108  10788  13572
 109  15660  11368
 110  15544  12760
 111   5336  18908
 112   6264  19140
 113  11832  17516
 114  10672  14152
 115  10208  15196
 116  12180  14848
 117  11020  10208
 118   7656  17052
 119  16240   8352
 120  10440  14732
 121   9164  15544
 122   8004  11020
 123   5684  11948
 124   9512  16472
 125  13688  17516
 126  11484   8468
 127   3248  14152