计算机视觉中Canny算子详解

---

前言

Canny边缘检测是一种非常流行的边缘检测算法，是John Canny在1986年提出的。它是一个多阶段的算法，即由多个步骤构成。本文主要讲解了Canny算子的原理及实现过程。

---

一、Canny的实现步骤

通常情况下边缘检测的目的是在保留原有图像属性的情况下，显著减少图像的数据规模。有多种算法可以进行边缘检测，虽然Canny算法年代久远，但可以说它是边缘检测的一种标准算法，而且仍在研究中广泛使用。

1. 应用高斯滤波来平滑图像，目的是去除噪声
2. 找寻图像的强度梯度（intensity gradients）
3. 应用非最大抑制（non-maximum suppression）技术来消除边误检（本来不是但检测出来是）
4. 应用双阈值的方法来决定可能的（潜在的）边界
5. 利用滞后技术来跟踪边界

二、具体实现

1.高斯平滑滤波

滤波是为了去除噪声，选用高斯滤波也是因为在众多噪声滤波器中，高斯表现最好（表现怎么定义的？最好好到什么程度？），你也可以试试其他滤波器如均值滤波、中值滤波等等。一个大小为(2k+1)x(2k+1)的高斯滤波器核（核一般都是奇数尺寸的）的生成方程式由下式给出：

下面是手动创建一个高斯滤波核的函数：

def gaussian_kernel(size, sigma):
    """ Implementation of Gaussian Kernel.

    This function follows the gaussian kernel formula,
    and creates a kernel matrix.

    Hints:
    - Use np.pi and np.exp to compute pi and exp.

    Args:
        size: int of the size of output matrix.
        sigma: float of sigma to calculate kernel.

    Returns:
        kernel: numpy array of shape (size, size).
    """

    kernel = np.zeros((size, size))

    ### YOUR CODE HERE
    for x in range(size):
        for y in range(size):
            kernel[x, y] = 1 / (2*np.pi*sigma*sigma) * np.exp(-(x*x+y*y)/(2*sigma*sigma))
    ### END YOUR CODE

    return kernel

这是定义卷积计算过程的函数：

def conv(image, kernel):
    """ An implementation of convolution filter.

    This function uses element-wise multiplication and np.sum()
    to efficiently compute weighted sum of neighborhood at each
    pixel.

    Args:
        image: numpy array of shape (Hi, Wi).
        kernel: numpy array of shape (Hk, Wk).

    Returns:
        out: numpy array of shape (Hi, Wi).
    """
    Hi, Wi = image.shape
    Hk, Wk = kernel.shape
    out = np.zeros((Hi, Wi))

    # For this assignment, we will use edge values to pad the images.
    # Zero padding will make derivatives at the image boundary very big,
    # whereas we want to ignore the edges at the boundary.
    pad_width0 = Hk // 2
    pad_width1 = Wk // 2
    pad_width = ((pad_width0,pad_width0),(pad_width1,pad_width1))
    padded = np.pad(image, pad_width, mode='edge')

    ### YOUR CODE HERE
    x = Hk // 2
    y = Wk // 2
    # 横向遍历卷积后的图像
    for i in range(pad_width0, Hi-pad_width0): 
        # 纵向遍历卷积后的图像
        for j in range(pad_width1, Wi-pad_width1): 
            split_img = image[i-pad_width0:i+pad_width0+1, j-pad_width1:j+pad_width1+1]
            # 对应元素相乘
            out[i, j] = np.sum(np.multiply(split_img, kernel))
    # out = (out-out.min()) * (1/(out.max()-out.min()) * 255).astype('uint8')
    ### END YOUR CODE

    return out

接下来就是用自己写的高斯滤波卷积核去卷原来的图片：

# Test with different kernel_size and sigma
kernel_size = 5
sigma = 1.4

# Load image
img = io.imread('iguana.png', as_gray=True)

# Define 5x5 Gaussian kernel with std = sigma
kernel = gaussian_kernel(kernel_size, sigma)

# Convolve image with kernel to achieve smoothed effect
smoothed = conv(img, kernel)

plt.subplot(1,2,1)
plt.imshow(img)
plt.title('Original image')
plt.axis('off')

plt.subplot(1,2,2)
plt.imshow(smoothed)
plt.title('Smoothed image')
plt.axis('off')

plt.show()

结果是下面两张图片，可以看到图像的边缘被明显地模糊了，图像的抗噪能力变强了。

总结一下这一步：高斯滤波其实就是将所指像素用周围的像素的某种均值代替(即卷积核)，卷积核尺寸越大，去噪能力越强，因此噪声越少，但图片越模糊，canny检测算法抗噪声能力越强，但模糊的副作用也会导致定位精度不高。
高斯的卷积核大小推荐：一般情况下，尺寸5 * 5，3 * 3也行。

2.计算梯度大小和方向

对于一张图片来说，梯度能很好地反映其像素的变化情况，而梯度变化越大，说明相邻像素之间存在着较大差异，放大到整张图片来说，就是在某一块区域存在边缘，从视觉上来说就是用黑到白(灰度图片读入)。
梯度的计算分为大小和方向，首先需要求出各个方向上的梯度，然后求平方根和切线。
以下是x、y方向上梯度的计算方式：

代码实现：

def partial_x(img):
    """ Computes partial x-derivative of input img.

    Hints:
        - You may use the conv function in defined in this file.

    Args:
        img: numpy array of shape (H, W).
    Returns:
        out: x-derivative image.
    """

    out = None

    ### YOUR CODE HERE
    # 对x求偏导
    kernel = np.array(([-1, 0, 1], [-1, 0, 1], [-1, 0, 1]))# np.random.randint(10, size=(3, 3))
    out = conv(img, kernel) / 2
    ### END YOUR CODE

    return out

def partial_y(img):
    """ Computes partial y-derivative of input img.

    Hints:
        - You may use the conv function in defined in this file.

    Args:
        img: numpy array of shape (H, W).
    Returns:
        out: y-derivative image.
    """

    out = None

    ### YOUR CODE HERE
    # 对y求偏导
    kernel = np.array(([1, 1, 1], [0, 0, 0], [-1, -1, -1]))# np.random.randint(10, size=(3, 3))
    out = conv(img, kernel) / 2
    ### END YOUR CODE
    
    return out
    
def gradient(img):
    """ Returns gradient magnitude and direction of input img.

    Args:
        img: Grayscale image. Numpy array of shape (H, W).

    Returns:
        G: Magnitude of gradient at each pixel in img.
            Numpy array of shape (H, W).
        theta: Direction(in degrees, 0 <= theta < 360) of gradient
            at each pixel in img. Numpy array of shape (H, W).

    Hints:
        - Use np.sqrt and np.arctan2 to calculate square root and arctan
    """
    G = np.zeros(img.shape)
    theta = np.zeros(img.shape)

    ### YOUR CODE HERE
    Gx = partial_x(img)
    Gy = partial_y(img)
    # 求梯度的大小(平方和的根号)
    G = np.sqrt(np.power(Gx, 2) + np.power(Gy, 2))
    theta = np.arctan2(Gy, Gx) * 180 / np.pi # 转换成角度制
    ### END YOUR CODE

    return G, theta

可以拿一张图片来测试一下：

# Compute partial derivatives of smoothed image
Gx = partial_x(smoothed)
Gy = partial_y(smoothed)

plt.subplot(1,2,1)
plt.imshow(Gx)
plt.title('Derivative in x direction')
plt.axis('off')

plt.subplot(1,2,2)
plt.imshow(Gy)
plt.title('Derivative in y direction')
plt.axis('off')

plt.show()

可以看到，[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]对应了x方向上的边缘检测(在碰到x方向垂直的边界的时候计算出来的数值更大，所以像素更亮)，[1, 1, 1], [0, 0, 0], [-1, -1, -1]同理对应了y方向上的边缘检测。
另外有45°和135°的边缘检测，我这里没有着手去实现，如果有兴趣可以去尝试一下，就是会出现不同方向上的边缘。

3.非极大抑制

用sobel算子或者是其他简单的边缘检测方法，计算出来的边缘太粗了，就是说原本的一条边用几条几乎重叠的边所代替了，导致视觉上看起来边界很粗。非极大抑制是一种瘦边经典算法。它抑制那些梯度不够大的像素点，只保留最大的梯度，从而达到瘦边的目的。
a) 将其梯度方向近似为以下值中的一个[0,45,90,135,180,225,270,315]（即上下左右和45度方向）这一步是为了方便使用梯度；
b) 比较该像素点，和其梯度方向正负方向的像素点的梯度强度，这里比较的范围一般为像素点的八邻域；
c) 如果该像素点梯度强度最大则保留，否则抑制(删除，即置为0)；

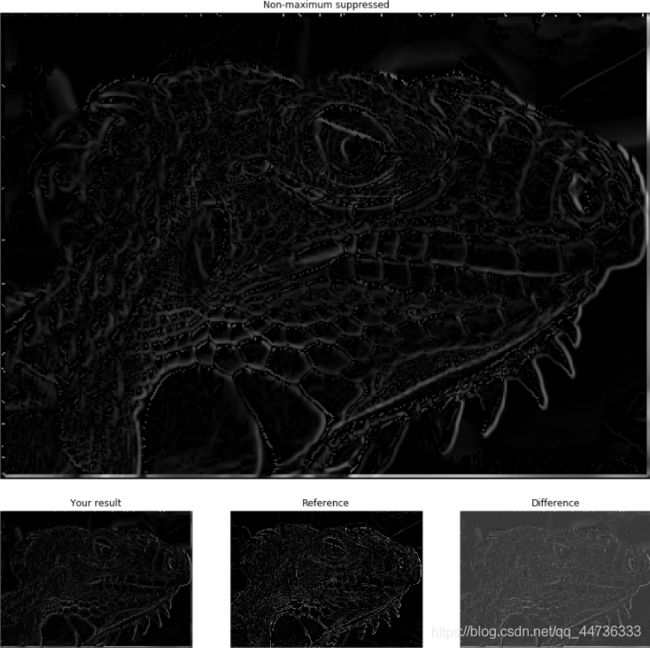
可以看到经过非极大抑制后，图像的边缘明显变细了，边界显得更加清晰了。
代码附上：

def non_maximum_suppression(G, theta):
    """ Performs non-maximum suppression.

    This function performs non-maximum suppression along the direction
    of gradient (theta) on the gradient magnitude image (G).

    Args:
        G: gradient magnitude image with shape of (H, W).
        theta: direction of gradients with shape of (H, W).

    Returns:
        out: non-maxima suppressed image.
    """
    H, W = G.shape
    out = np.zeros((H, W))
    
    # 将角度近似到45°的对角线, 正负无所谓, 只看对角线跟水平垂直
    # Round the gradient direction to the nearest 45 degrees
    theta = np.floor((theta + 22.5) / 45) * 45

    ### BEGIN YOUR CODE
    anchor = np.stack(np.where(G!=0)).T  # 获取非零梯度的位置    
    for x, y in anchor:
        center_point = G[x, y]
        current_theta = theta[x, y]
        dTmp1 = 0
        dTmp2 = 0
        W = 0
        if current_theta >= 0 and current_theta < 45:
            g1, g2, g3, g4 = G[x + 1, y - 1], G[x + 1, y], G[x - 1, y + 1], G[x - 1, y]
            W = abs(np.tan(current_theta*np.pi/180))  # tan0-45范围为0-1
            dTmp1 = W * g1 + (1-W) * g2
            dTmp2 = W * g3 + (1-W) * g4
        elif current_theta >= 45 and current_theta < 90:
            g1, g2, g3, g4 = G[x+1, y-1], G[x, y-1], G[x-1, y+1], G[x, y+1]
            W = abs(np.tan((current_theta-90)*np.pi/180))
            dTmp1 = W * g1 + (1-W) * g2
            dTmp2 = W * g3 + (1-W) * g4
        elif current_theta >= -90 and current_theta < -45:
            g1, g2, g3, g4 = G[x-1, y-1], G[x, y-1], G[x+1, y+1], G[x, y+1]
            W = abs(np.tan((current_theta-90)*np.pi/180))
            dTmp1 = W * g1 + (1-W) * g2
            dTmp2 = W * g3 + (1-W) * g4
        elif current_theta>=-45 and current_theta<0:
            g1, g2, g3, g4 = G[x+1, y+1], G[x+1, y], G[x-1, y-1], G[x-1, y]
            W = abs(np.tan(current_theta * np.pi / 180))
            dTmp1 = W * g1 + (1-W) * g2
            dTmp2 = W * g3 + (1-W) * g4
        if dTmp1 < center_point and dTmp2 < center_point:   
                out[x,y]=center_point
    return out

4.双阈值(Double Thresholding)和滞后边界跟踪

经过非极大抑制后图像中仍然有很多噪声点。Canny算法中应用了一种叫双阈值的技术。
即设定一个阈值上界和阈值下界（opencv中通常由人为指定的），图像中的像素点如果大于阈值上界则认为必然是边界（称为强边界，strong edge），小于阈值下界则认为必然不是边界，两者之间的则认为是候选项（称为弱边界，weak edge），需进行进一步处理。我查阅资料，了解到上界一般是下界的2-3倍，实现出来的效果比较好。

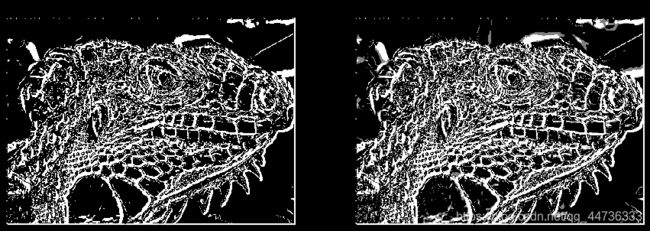
上图中，左边的是经过上界筛选的强边界，即肯定是边界；右边的是结果是强边界加上0.5权重的弱边界所呈现的效果(展示弱边界没有啥意义)。可以看到相较于之前的非极大抑制，双阈值的算法很大程度上提取到了真正的边界(但是对于不同的图片有不同的阈值参数)。
代码附上：

def double_thresholding(img, high, low):
    """
    Args:
        img: numpy array of shape (H, W) representing NMS edge response.
        high: high threshold(float) for strong edges.
        low: low threshold(float) for weak edges.

    Returns:
        strong_edges: Boolean array representing strong edges.
            Strong edeges are the pixels with the values greater than
            the higher threshold.
        weak_edges: Boolean array representing weak edges.
            Weak edges are the pixels with the values smaller or equal to the
            higher threshold and greater than the lower threshold.
    """

    strong_edges = np.zeros(img.shape, dtype=np.bool)
    weak_edges = np.zeros(img.shape, dtype=np.bool)

    ### YOUR CODE HERE
    H, W = img.shape
    for i in range(0, H):
        for j in range(0, W):
            if img[i, j] > high:
                strong_edges[i, j] = True
            elif img[i, j] >= low:
                weak_edges[i, j] = True
    ### END YOUR CODE

    return strong_edges, weak_edges

可以肯定的是，强边缘必然是边缘点，因此必须将T1设置的足够高，以要求像素点的梯度值足够大（变化足够剧烈），而弱边缘可能是边缘，也可能是噪声，如何判断呢？当弱边缘的周围8邻域有强边缘点存在时，就将该弱边缘点变成强边缘点，以此来实现对强边缘的补充。

滞后边界跟踪(对弱边缘的二次判断)，代码如下：

def get_neighbors(y, x, H, W):
    """ Return indices of valid neighbors of (y, x).

    Return indices of all the valid neighbors of (y, x) in an array of
    shape (H, W). An index (i, j) of a valid neighbor should satisfy
    the following:
        1. i >= 0 and i < H
        2. j >= 0 and j < W
        3. (i, j) != (y, x)

    Args:
        y, x: location of the pixel.
        H, W: size of the image.
    Returns:
        neighbors: list of indices of neighboring pixels [(i, j)].
    """
    neighbors = []

    for i in (y-1, y, y+1):
        for j in (x-1, x, x+1):
            if i >= 0 and i < H and j >= 0 and j < W:
                if (i == y and j == x):
                    continue
                neighbors.append((i, j))

    return neighbors


def link_edges(strong_edges, weak_edges):
    """ Find weak edges connected to strong edges and link them.

    Iterate over each pixel in strong_edges and perform breadth first
    search across the connected pixels in weak_edges to link them.
    Here we consider a pixel (a, b) is connected to a pixel (c, d)
    if (a, b) is one of the eight neighboring pixels of (c, d).

    Args:
        strong_edges: binary image of shape (H, W).
        weak_edges: binary image of shape (H, W).
    
    Returns:
        edges: numpy boolean array of shape(H, W).
    """

    H, W = strong_edges.shape
    # 获取强边界的非零元素坐标，一行为一组坐标
    indices = np.stack(np.nonzero(strong_edges)).T
    print(indices)
    edges = np.zeros((H, W), dtype=np.bool)

    # Make new instances of arguments to leave the original
    # references intact
    weak_edges = np.copy(weak_edges)
    edges = np.copy(strong_edges)

    ### YOUR CODE HERE
    for (x, y) in indices:
        neighbors = get_neighbors(x, y, H, W)
        edges[x, y] = True
        for neighbor in neighbors:
            if weak_edges[neighbor]:
                edges[neighbor] = True
    ### END YOUR CODE

    return edges

可以拿一个简单的例子来测试一下算法的正确性：

'''
我们假设两类边缘：经过非极大值抑制之后的边缘点中，梯度值超过T1的称为强边缘，梯度值小于T1大于T2的称为弱边缘，梯度小于T2的不是边缘。
可以肯定的是，强边缘必然是边缘点，因此必须将T1设置的足够高，以要求像素点的梯度值足够大（变化足够剧烈），而弱边缘可能是边缘，也可能是噪声，如何判断呢？
当弱边缘的周围8邻域有强边缘点存在时，就将该弱边缘点变成强边缘点，以此来实现对强边缘的补充。
实际中人们发现T1:T2=2:1的比例效果比较好，其中T1可以人为指定，也可以设计算法来自适应的指定，比如定义梯度直方图的前30%的分界线为T1，我实现的是人为指定阈值。
检查8邻域的方法叫边缘滞后跟踪，连接边缘的办法还有区域生长法等等。
'''
from edge import get_neighbors, link_edges

test_strong = np.array(
    [[1, 0, 0, 0],
     [0, 0, 0, 0],
     [0, 0, 0, 0],
     [0, 0, 0, 1]],
    dtype=np.bool
)

test_weak = np.array(
    [[0, 0, 0, 1],
     [0, 1, 0, 0],
     [1, 0, 0, 0],
     [0, 0, 1, 0]],
    dtype=np.bool
)

test_linked = link_edges(test_strong, test_weak)

plt.subplot(1, 3, 1)
plt.imshow(test_strong)
plt.title('Strong edges')

plt.subplot(1, 3, 2)
plt.imshow(test_weak)
plt.title('Weak edges')

plt.subplot(1, 3, 3)
plt.imshow(test_linked)
plt.title('Linked edges')
plt.show()

在上图中，白色方块代表存在边缘(包括强弱边缘)，遍历弱边缘中的每个像素，如果像素的八邻域存在强边缘对应的像素，则将这个弱边缘像素归为真正的边缘(从视觉上来理解，就是存在一条不确定的边缘，如果这条不确定的边缘旁存在真正的边缘，则将这条边归为真边，非则就将其删除)


可以看到相较于只保留弱边缘的效果图，滞后边界跟踪算法保留了更多的边缘细节。

整理一下整个算法，我们将Canny算子归纳到一个函数，调用一下看一下效果：

def canny(img, kernel_size=5, sigma=1.4, high=20, low=15):
    """ Implement canny edge detector by calling functions above.

    Args:
        img: binary image of shape (H, W).
        kernel_size: int of size for kernel matrix.
        sigma: float for calculating kernel.
        high: high threshold for strong edges.
        low: low threashold for weak edges.
    Returns:
        edge: numpy array of shape(H, W).
    """
    ### YOUR CODE HERE
    # 高斯模糊
    kernel = gaussian_kernel(kernel_size, sigma)
    img = conv(img, kernel)
    #io.imshow(color.gray2rgb(img))
    # 计算梯度Prewitt算子
    G, theta = gradient(img)
    #io.imshow(color.gray2rgb(G))
    # 非极大值抑制
    G = non_maximum_suppression(G, theta)
    #io.imshow(color.gray2rgb(G))

    # 双阈值抑制
    strong_edges, weak_edges = double_thresholding(G, high, low)
    # 连通边
    edge = link_edges(strong_edges, weak_edges)
    ### END YOUR CODE

    return edge

from edge import canny

# Load image
img = io.imread('iguana.png', as_gray=True)

# Run Canny edge detector
edges = canny(img, kernel_size=5, sigma=1.4, high=0.03, low=0.02)
print (edges.shape)

plt.subplot(1, 3, 1)
plt.imshow(edges)
plt.axis('off')
plt.title('Your result')

plt.subplot(1, 3, 2)
reference = np.load('references/iguana_canny.npy')
plt.imshow(reference)
plt.axis('off')
plt.title('Reference')

plt.subplot(1, 3, 3)
plt.imshow(edges ^ reference)
plt.title('Difference')
plt.axis('off')
plt.show()

---

总结

这次写整个Canny算法其实遇到了很多坑，比如角度弧度换算那里，课件上写得很模糊，后来查阅资料才理清楚的。其次就是弱边界判断那里，我一开始对应每一个像素都要遍历整张图片的梯度方向，然后时间复杂度太大了，其实只要遍历八邻域就可以了。最后就是写代码一定要一定要细心，虽然python相较于c有很多东西都已经帮你写好了，但是还是要注意类似list下标之类的问题。
差不多就这样啦~