MATLAB--多项式与拟合与插值
多项式连续可导,可积的。
用行向量表示
>> p=[9 7 -2 0 0 4]; >> F=poly2sym(p) F = 9*x^5 + 7*x^4 - 2*x^3 + 4poly2sym:转化为手写多项式形式
四则运算(加减要最高次等长;conv卷积-多项式乘法;多项式除法-反卷积deconv)
>> p1=[3 -5 2 -7 5 6]; p2=[0 0 0 3 5 -3]; f1=poly2sym(p1+p2) f1 = 3*x^5 - 5*x^4 + 2*x^3 - 4*x^2 + 10*x + 3多项式乘法
>> f2=poly2sym(conv(p1,p2)) f2 = 9*x^7 - 28*x^5 + 4*x^4 - 26*x^3 + 64*x^2 + 15*x - 18除法(商多项式和余数多项式)
>> p2=[3 5 -3]; >> f3=poly2sym(deconv(p1,p2)) f3 = x^3 - (10*x^2)/3 + (65*x)/9 - 478/27 >> [P,Q]=deconv(p1,p2) P = 1.0000 -3.3333 7.2222 -17.7037 Q = 0 0 0 0 115.1852 -47.1111
roots:求多项式的根;poly:生成指定根的多项式(非线性方程求根:fzero、fminbnd)
>> p=[3 0 4 -5 -7.2 5];
>> r=roots(p)
r =
-0.3046 + 1.6217i
-0.3046 - 1.6217i
-1.0066 + 0.0000i
1.0190 + 0.0000i
0.5967 + 0.0000i
>> R=[-2 2];
Fx=poly2sym(poly(R))
Fx =
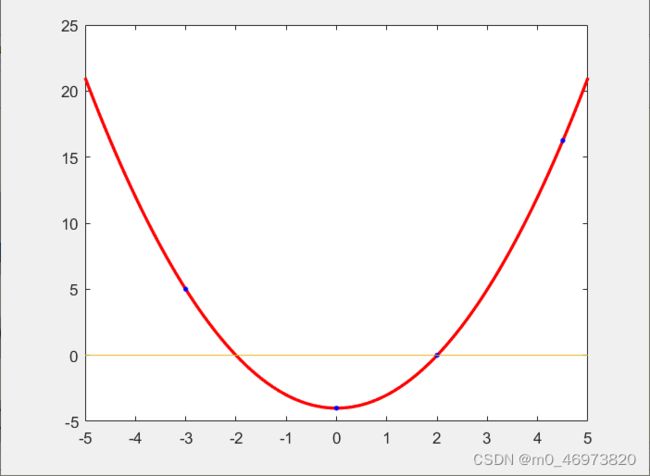
x^2 - 4polyval:计算多项式在任意点的值
>> Fx=poly(R)
x=[-3 2 0 4.5];
Y=polyval(Fx,x)
Fx =
1 0 -4
Y =
5.0000 0 -4.0000 16.2500显示
X=-5:0.01:5;
Y=polyval(Fx,X);
plot(X,Y,'r-','LineWidth',2)
hold on;
plot(x,y,'b.','MarkerSize',10)
hold on;
f=@(x)0;fplot(f);p=poly(A)如果A是一个方阵,返回的p是一个n+1个元素的行向量,表示A的特征多项式的系数。
polyvalm(P,A)这是矩阵的多项式
>> A=magic(2); >> p=[2 -1 5]; >> polyvalm(p,A) ans = 30 15 20 35 >> 2*A^2-A+5*eye(2) ans = 30 15 20 35
多项式求导polyder()多项式的积分polyint()
>> p=[3 -5 2 6 10]; %3*x^4 - 5*x^3 + 2*x^2 + 6*x + 10 pd=poly2sym(polyder(p)) pd = 12*x^3 - 15*x^2 + 4*x + 6 >> pi=poly2sym(polyint(p)) pi = (3*x^5)/5 - (5*x^4)/4 + (2*x^3)/3 + 3*x^2 + 10*x
数据拟合
生成采样点
x=0:0.2:10;
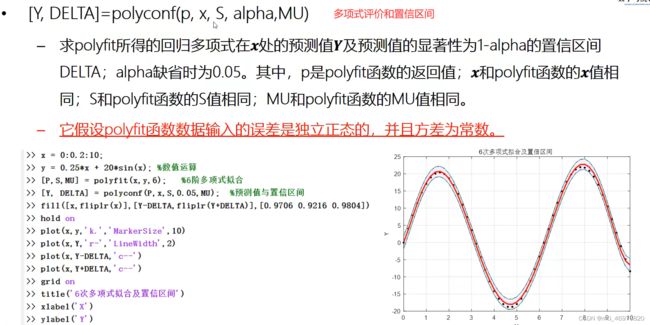
y=0.25*x+20*sin(x);拟合5次多项式
[P5,S5,mu5]=polyfit(x,y,5);
y5=polyval(P5,x,S5,mu5);显示
plot(x,y,'k.','MarkerSize',15);
grid on
hold on;plot(x,y5,'b-');
legend('采样点','5次多项式','Location','best')
legend('boxoff')%% 置信区间
[Y,DELTA]=polyconf(P5,x,S5,0.05,mu5);
plot(x,Y-DELTA,'m--');plot(x,Y+DELTA,'m--');%% 非线性拟合函数(自定义拟合)nlinfit()
data=xlsread('nlinfit_data.xlsx');
x=data(1,:)';
y=data(2,:)';
plot(x,y,'k.','MarkerSize',15)
%% 定义一个函数
beta0=[0.3 0.1];
beta=nlinfit(x,y,'nlinfun',beta0)
yp=nlinfun(beta,x);
hold on;plot(x,yp,'b-','LineWidth',2);要给一个初值,和自定义函数