机器学习----多项式回归

多项式回归简介

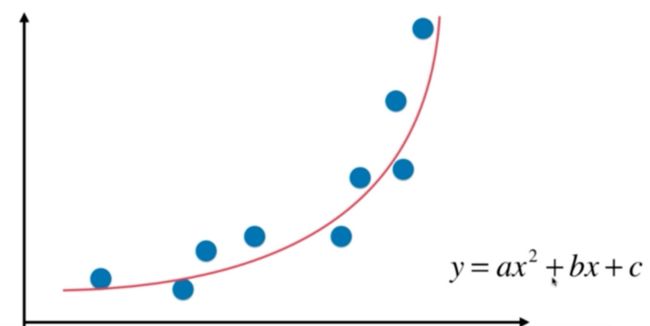
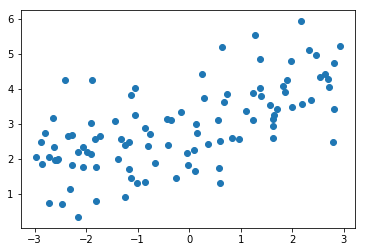
考虑下面的数据，虽然我们可以使用线性回归来拟合这些数据，但是这些数据更像是一条二次曲线,相应的方程是y=ax2+bx+c,这是式子虽然可以理解为二次方程，但是我们呢可以从另外一个角度来理解这个式子：

如果将x2理解为一个特征，将x理解为另外一个特征,换句话说，本来我们的样本只有一个特征x，现在我们把他看成有两个特征的一个数据集。多了一个特征x2，那么从这个角度来看，这个式子依旧是一个线性回归的式子，但是从x的角度来看，他就是一个二次的方程

以上这样的方式，就是所谓的多项式回归

相当于我们为样本多添加了一些特征，这些特征是原来样本的多项式项，增加了这些特征之后，我们们可以使用线性回归的思路更好的我们的数据

什么是多项式回归

import numpy as np 
import matplotlib.pyplot as plt

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
# 一元二次方程
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

plt.scatter(x, y)
plt.show()

线性回归？

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)

plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

很明显，我们用一跟直线来拟合一根有弧度的曲线，效果是不好的

解决方案， 添加一个特征

原来所有的数据都在X中，现在对X中每一个数据都进行平方，
再将得到的数据集与原数据集进行拼接，
在用新的数据集进行线性回归

X2 = np.hstack([X, X**2])

X2.shape

(100, 2)

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

plt.scatter(x, y)
# 由于x是乱的，所以应该进行排序
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

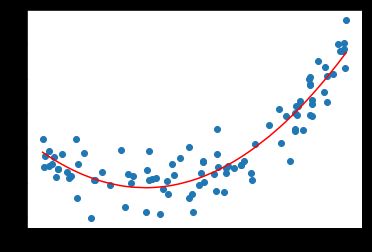
从上图可以看出，当我们添加了一个特征（原来特征的平方）之后，再从x的维度来看，就形成了一条曲线，显然这个曲线对原来数据集的拟合程度是更好的

# 第一个系数是x前面的系数，第二个系数是x平方前面的系数
lin_reg2.coef_

array([ 0.99870163,  0.54939125])

lin_reg2.intercept_

1.8855236786516001

3.总结
多线性回归在机器学习算法上并没有新的地方，完全是使用线性回归的思路
他的关键在于为原来的样本，添加新的特征。而我们得到新的特征的方式是原有特征的多项式的组合。
采用这样的方式，我们就可以解决一些非线性的问题

与此同时需要主要，我们在上一章所讲的PCA是对我们的数据进行降维处理，而我们这一章所讲的多项式回归显然在做一件相反的事情，他让我们的数据升维，在升维之后使得我们的算法可以更好的拟合高纬度的数据

scikit-learn中的多项式回归和Pipeline

import numpy as np 
import matplotlib.pyplot as plt

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

# sklearn中对数据进行预处理的函数都封装在preprocessing模块下，包括之前学的归一化StandardScaler
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree=2)  # 表示为数据的特征最多添加2次幂
poly.fit(X)
X2 = poly.transform(X)

X2.shape

(100, 3)

X[:5,:]

array([[ 0.14960154],
       [ 0.49319423],
       [-0.87176575],
       [-1.33024477],
       [ 0.47383199]])

# 第一列是sklearn为我们添加的X的零次方的特征
# 第二列和原来的特征一样是X的一次方的特征
# 第三列是添加的X的二次方的特征
X2[:5,:]

array([[ 1.        ,  0.14960154,  0.02238062],
       [ 1.        ,  0.49319423,  0.24324055],
       [ 1.        , -0.87176575,  0.75997552],
       [ 1.        , -1.33024477,  1.76955114],
       [ 1.        ,  0.47383199,  0.22451675]])

from sklearn.linear_model import LinearRegression

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

lin_reg2.coef_

array([ 0.        ,  0.9460157 ,  0.50420543])

lin_reg2.intercept_

2.1536054095953823

关于PolynomialFeatures

X = np.arange(1, 11).reshape(-1, 2)

X

array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10]])

poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)

X2.shape

(5, 6)

X2

array([[   1.,    1.,    2.,    1.,    2.,    4.],
       [   1.,    3.,    4.,    9.,   12.,   16.],
       [   1.,    5.,    6.,   25.,   30.,   36.],
       [   1.,    7.,    8.,   49.,   56.,   64.],
       [   1.,    9.,   10.,   81.,   90.,  100.]])

将5行2列的矩阵进行多项式转换后变成了5行6列

第一列是1 对应的是0次幂
第二列和第三列对应的是原来的x矩阵，此时他有两列一次幂的项
第四列是原来数据的第一列平方的结果
第六列是原来数据的第二列平方的结果
第五列是原来数据的两列相乘的结果
可以想象如果将degree设置为3，那么将产生一下10个元素

也就是说PolynomialFeatures会穷举出所有的多项式组合

Pipeline

pipline的英文名字是管道，那么 我们如何使用管道呢，先考虑我们多项式回归的过程

1.使用PolynomialFeatures生成多项式特征的数据集
2.如果生成数据幂特别的大，那么特征直接的差距就会很大，导致我们的搜索非常慢，这时候可以进行数据归一化
3.进行线性回归
pipline 的作用就是把上面的三个步骤合并，使得我们不用一直重复这三步

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 传入每一步的对象名和类的实例化
poly_reg = Pipeline([
    ("poly", PolynomialFeatures(degree=2)),
    ("std_scaler", StandardScaler()),
    ("lin_reg", LinearRegression())
])

poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

过拟合和欠拟合

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

使用线性回归

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)

0.49537078118650091

y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

使用均方误差来看拟合的结果，这是因为我们同样都是对一组数据进行拟合，所以使用不同的方法对数据进行拟合
得到的均方误差的指标是具有可比性的。

from sklearn.metrics import mean_squared_error

y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)

3.0750025765636577

使用多项式回归

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)

Pipeline(steps=[('poly', PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)), ('std_scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('lin_reg', LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False))])

y2_predict = poly2_reg.predict(X)
# 显然使用多项式回归得到的结果是更好的
mean_squared_error(y, y2_predict)

1.0987392142417856

plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()

poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X, y)

y10_predict = poly10_reg.predict(X)
mean_squared_error(y, y10_predict)

1.0508466763764164

plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()

poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)

y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)

0.68743577834336944

plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()

这条曲线只是原来随机生成的点（分布不均匀）对应的y的预测值连接起来的曲线，不过有x轴很多地方可能没有数据点，所以连接的结果和原来的曲线不一样（不是真实的y曲线）。
下面尝试真正还原原来的曲线（构造均匀分布的原数据集）

X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(X_plot)

plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])  # 必须指定
plt.show()

总有一条曲线，他能拟合所有的样本点，使得均方误差的值为0
degree从2到10到100的过程中，虽然均方误差是越来越小的，从均方误差的角度来看是更加小的
但是他真的能更好的预测我们数据的走势吗，例如我们选择2.5到3的一个x，使用上图预测出来的y的大小（0或者-1之间）显然不符合我们的数据

换句话说，我们使用了一个非常高维的数据，虽然使得我们的样本点获得了更小的误差，但是这根曲线完全不是我们想要的样子
他为了拟合我们所有的样本点，变的太过复杂了，这种情况就是过拟合【over-fitting】

相反，在最开始，我们直接使用一根直线来拟合我们的数据，也没有很好的拟合我们的样本特征，当然他犯的错误不是太过复杂了，而是太过简单了
这种情况，我们成为欠拟合-【under-fitting】

对于现在的数据（基于二次方程构造），我们使用低于2项的拟合结果，就是欠拟合；高于2项的拟合结果，就是过拟合

为什么要使用训练数据集和测试数据集

模型的泛化能力

使用上节的过拟合结果，我们可以得知，虽然我们训练出的曲线将原来的样本点拟合的非常好，总体的误差非常的小， 但是一旦来了新的样本点，他就不能很好的预测了，在这种情况下，我们就称我们得到的这条弯弯曲曲的曲线，他的**泛化能力（由此及彼的能力）**非常弱

image.png

训练数据集和测试数据集的意义

我们训练的模型目的是为了使得预测的数据能够尽肯能的准确，在这种情况下，我们观察训练数据集的拟合程度是没有意义的 我们真正需要的是，我们得到的模型的泛化能力更高，解决这个问题的方法也就是使用训练数据集，测试数据集的分离

测试数据对于我们的模型是全新的数据，如果使用训练数据获得的模型面对测试数据也能获得很好的结果，那么我们就说我们的模型泛化能力是很强的。 如果我们的模型面对测试数据结果很差的话，那么他的泛化能力就很弱。事实上，这是训练数据集更大的意义

train test split的意义

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
mean_squared_error(y_test, y_predict)

2.2199965269396573

poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X_train, y_train)
y2_predict = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)

0.80356410562978997

poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X_train, y_train)
y10_predict = poly10_reg.predict(X_test)
mean_squared_error(y_test, y10_predict)

0.92129307221507939

poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X_train, y_train)
y100_predict = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict)

14075796419.234262

刚刚我们进行的实验实际上在实验模型的复杂度，对于多项式模型来说，我们回归的阶数越高，我们的模型会越复杂，在这种情况下对于我们的机器学习算法来说，通常是有下面一张图的。横轴是模型复杂度（对于不同的算法来说，代表的是不同的意思，比如对于多项式回归来说，是阶数越高，越复杂；对于KNN来说，是K越小，模型越复杂，k越大，模型最简单，当k=n的时候，模型就简化成了看整个样本里，哪种样本最多，当k=1来说，对于每一个点，都要找到离他最近的那个点），另一个维度是模型准确率（也就是他能够多好的预测我们的曲线）

通常对于这样一个图，会有两根曲线：

• 一个是对于训练数据集来说的，模型越复杂，模型准确率越高，因为模型越复杂，对训练数据集的拟合就越好，相应的模型准确率就越高
• 对于测试数据集来说，在模型很简单的时候，模型的准确率也比较低，随着模型逐渐变复杂，对测试数据集的准确率在逐渐的提升，提升到一定程度后，如果模型继续变复杂，那么我们的模型准确率将会进行下降（欠拟合->正合适->过拟合）

欠拟合和过拟合的标准定义

欠拟合：算法所训练的模型不能完整表述数据关系 过拟合：算法所训练的模型过多的表达了数据间的噪音关系

学习曲线

随着训练样本的逐渐增多，算法训练出的模型的表现能力

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

学习曲线

实际编程实现学习曲线

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=10)

X_train.shape

(75, 1)

2.1观察线性回归的学习曲线：观察线性回归模型，随着训练数据集增加，性能的变化

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

train_score = []
test_score = []
for i in range(1, 76):
    lin_reg = LinearRegression()
    lin_reg.fit(X_train[:i], y_train[:i])
    
    y_train_predict = lin_reg.predict(X_train[:i])
    train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
    y_test_predict = lin_reg.predict(X_test)
    test_score.append(mean_squared_error(y_test, y_test_predict))

plt.plot([i for i in range(1, 76)], np.sqrt(train_score), label="train")
plt.plot([i for i in range(1, 76)], np.sqrt(test_score), label="test")
plt.legend()
plt.show()

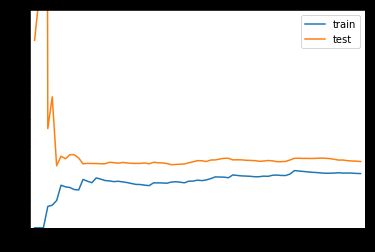
从趋势上看：

在训练数据集上，误差是逐渐升高的。这是因为我们的训练数据越来越多，我们的数据点越难得到全部的累积，不过整体而言，在刚开始的时候误差变化的比较快，后来就几乎不变了
在测试数据集上，在使用非常少的样本进行训练的时候，刚开始我们的测试误差非常的大，当训练样本大到一定程度以后，我们的测试误差就会逐渐减小，减小到一定程度后，也不会小太多，达到一种相对稳定的情况
在最终，测试误差和训练误差趋于相等，不过测试误差还是高于训练误差一些，这是因为，训练数据在数据非常多的情况下，可以将数据拟合的比较好，误差小一些，但是泛化到测试数据集的时候，还是有可能多一些误差

def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
    
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))
        
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(test_score), label="test")
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 4])
    plt.show()
    
plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test)

from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)

首先整体从趋势上，和线性回归的学习曲线是类似的
仔细观察，和线性回归曲线的不同在于，线性回归的学习曲线1.5，1.8左右；2阶多项式回归稳定在了1.0，0.9左右,2阶多项式稳定的误差比较低，说明使用二阶线性回归的性能是比较好的

poly20_reg = PolynomialRegression(degree=20)
plot_learning_curve(poly20_reg, X_train, X_test, y_train, y_test)

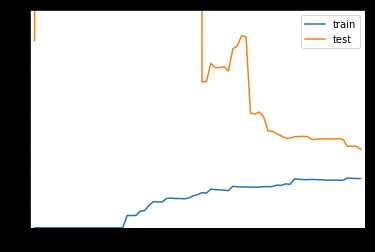
在使用20阶多项式回归训练模型的时候可以发现，在数据量偏多的时候，我们的训练数据集拟合的是比较好的，但是测试数据集的误差相对来说增大了很多，离训练数据集比较远，通常这就是过拟合的结果，他的泛化能力是不够的

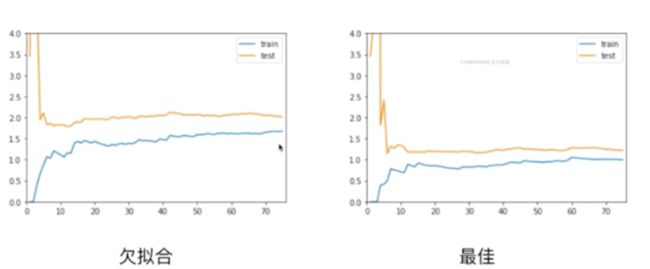
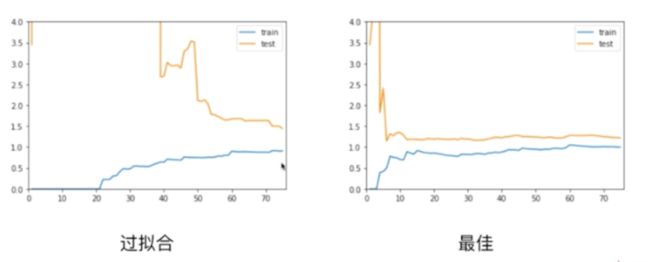
总结

对于欠拟合比最佳的情况趋于稳定的那个位置要高一些，说明无论对于训练数据集还是测试数据集来说，误差都比较大。这是因为我们本身模型选的就不对，所以即使在训练数据集上，他的误差也是大的，所以才会呈现出这样的一种形态

对于过拟合的情况，在训练数据集上，他的误差不大，和最佳的情况是差不多的，甚至在极端情况，如果degree取更高的话，那么训练数据集的误差会更低，但是问题在于，测试数据集的误差相对是比较大的，并且训练数据集的误差和测试数据集的误差相差比较大（表现在图上相差比较远），这就说明了此时我们的模型的泛化能力不够好，他的泛化能力是不够的

验证数据集与交叉验证

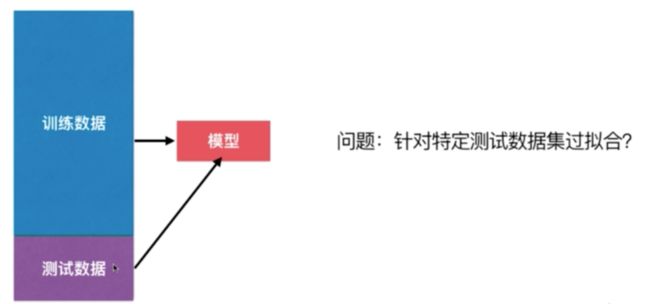
使用分割训练数据集和测试数据集来判断我们的机器学习性能的好坏，虽然是一个非常好的方案，但是会产生一个问题：针对特定测试数据集过拟合

我们每次使用测试数据来分析性能的好坏。一旦发现结果不好，我们就换一个参数（可能是degree也可能是其他超参数）重新进行训练。这种情况下，我们的模型在一定程度上围绕着测试数据集打转。也就是说我们在寻找一组参数，使得这组参数训练出来的模型在测试结果集上表现的最好。但是由于这组测试数据集是已知的，我们相当于在针对这组测试数据集进行调参，那么他也有可能产生过拟合的情况，也就是我们得到的模型针对测试数据集过拟合了

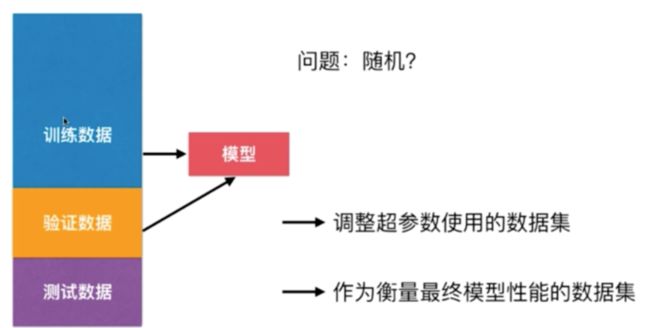
那么怎么解决这个问题呢？ 解决的方式其实就是：我们需要将我们的问题分为三部分，这三部分分别是训练数据集，验证数据集，测试数据集。 我们使用训练数据集训练好模型之后，将验证数据集送给这个模型，看看这个训练数据集训练的效果是怎么样的，如果效果不好的话，我们重新换参数，重新训练模型。直到我们的模型针对验证数据来说已经达到最优了。 这样我们的模型达到最优以后，再讲测试数据集送给模型，这样才能作为衡量模型最终的性能。换句话说，我们的测试数据集是不参与模型的创建的，而其他两个数据集都参与了训练。但是我们的测试数据集对于模型是完全不可知的，相当于我们在模型这个模型完全不知道的数据

这种方法还会有一个问题。由于我们的模型可能会针对验证数据集过拟合，而我们只有一份验证数据集，一旦我们的数据集里有比较极端的情况，那么模型的性能就会下降很多，那么为了解决这个问题，就有了交叉验证。

交叉验证 Cross Validation

交叉验证相对来说是比较正规的、比较标准的在我们调整我们的模型参数的时候看我们的性能的方式

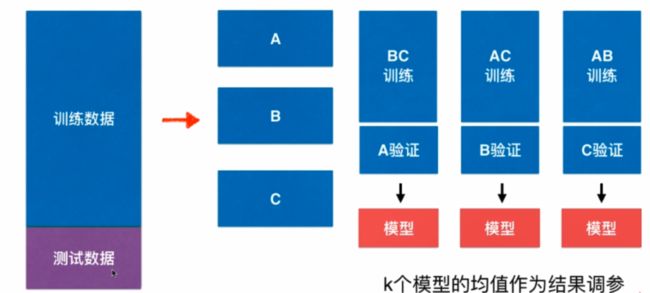
交叉验证：在训练模型的时候，通常把数据分成k份，例如分成3份（ABC）（分成k分，k属于超参数），这三份分别作为验证数据集和训练数据集。这样组合后可以分别产生三个模型，这三个模型，每个模型在测试数据集上都会产生一个性能的指标，这三个指标的平均值作为当前这个算法训练处的模型衡量的标准是怎样的。 由于我们有一个求平均的过程，所以不会由于一份验证数据集中有比较极端的数据而导致模型有过大的偏差，这比我们只分成训练、验证、测试数据集要更加准确

Validation 和 Cross Validation

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target

测试train_test_split

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)

from sklearn.neighbors import KNeighborsClassifier

best_k, best_p, best_score = 0, 0, 0
# k为k近邻中的寻找k个最近元素
for k in range(2, 11):
# p为明科夫斯基距离的p
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

Best K = 3
Best P = 4
Best Score = 0.986091794159

使用交叉验证

# 使用sklearn提供的交叉验证
from sklearn.model_selection import cross_val_score

knn_clf = KNeighborsClassifier()
# 返回的是一个数组，有三个元素，说明cross_val_score方法默认将我们的数据集分成了三份
# 这三份数据集进行交叉验证后产生了这三个结果

# cv默认为3，可以修改改参数，修改修改不同分数的数据集
cross_val_score(knn_clf,X_train,y_train,cv=3)

array([ 0.98895028,  0.97777778,  0.96629213])

best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        scores = cross_val_score(knn_clf, X_train, y_train)
        score = np.mean(scores)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

Best K = 2
Best P = 2
Best Score = 0.982359987401

通过观察两组调参过程的结果可以发现
1.两组调参得出的参数结果是不同的，通常这时候我们更愿意详细使用交叉验证的方式得出的结果。
因为使用train_test_split很有可能只是过拟合了测试数据集得出的结果
2.使用交叉验证得出的最好分数0.982是小于使用分割训练测试数据集得出的0.986，因为在交叉验证的
过程中，通常不会过拟合某一组的测试数据，所以平均来讲这个分数会稍微低一些

但是使用交叉验证得到的最好参数Best_score并不是真正的最好的结果，我们使用这种方式只是为了拿到
一组超参数而已，拿到这组超参数后我们就可以训练处我们的最佳模型

knn_clf = KNeighborsClassifier(weights='distance',n_neighbors=2,p=2)
# 用我们找到的k和p。来对X_train,y_train整体fit一下，来看他对X_test,y_test的测试结果
knn_clf.fit(X_train,y_train)
# 注意这个X_test,y_test在交叉验证过程中是完全没有用过的，也就是说我们这样得出的结果是可信的
knn_clf.score(X_test,y_test)

0.98052851182197498

回顾网格搜索

我们上面的操作，实际上在网格搜索的过程中已经进行了，只不过这个过程是sklean的网格搜索自带的一个过程

from sklearn.model_selection import GridSearchCV

param_grid = [
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(2, 11)], 
        'p': [i for i in range(1, 6)]
    }
]

grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)

Fitting 3 folds for each of 45 candidates, totalling 135 fits


[Parallel(n_jobs=1)]: Done 135 out of 135 | elapsed:  1.9min finished

的意思就是交叉验证中分割了三组数据集，而我们的参数组合为9*6=45中组合
3组数据集，45种组合，一共要进行135次的训练.

    GridSearchCV(cv=None, error_score='raise',
           estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
               metric_params=None, n_jobs=1, n_neighbors=10, p=5,
               weights='distance'),
           fit_params={}, iid=True, n_jobs=1,
           param_grid=[{'weights': ['distance'], 'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
           pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
           scoring=None, verbose=1)

grid_search.best_score_

0.98237476808905377

grid_search.best_params_

{'n_neighbors': 2, 'p': 2, 'weights': 'distance'}

best_knn_clf = grid_search.best_estimator_
best_knn_clf.score(X_test, y_test)

0.98052851182197498

cv参数

cross_val_score(knn_clf, X_train, y_train, cv=5)

array([ 0.99543379,  0.96803653,  0.98148148,  0.96261682,  0.97619048])

# cv默认为3，可以修改改参数，修改修改不同分数的数据集
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1, cv=5)

总结

虽然整体速度慢了，但是这个结果却是可信赖的

模型正则化-Regularization

什么是模型正则化

下图是我们之前使用多项式回归过拟合一个样本的例子，可以看到这条模型曲线非常的弯曲，而且非常的陡峭，可以想象这条曲线的一些θ系数会非常的大。 模型正则化需要做的事情就是限制这些系数的大小

模型正则化基本原理

一些需要注意的细节：

1. 对于θ的求和i是从1到n,没有将θ0加进去，因为他不是任意一项的系数，他只是一个截距，决定了整个曲线的高低，但是不决定曲线每一部分的陡峭和缓和。
2. θ求和的系数二分之一是一个惯例，加不加都可以，加上的原因是因为，将来对θ2>求导的时候可以抵消系数2，方便计算。不要也是可以的。
3. α实际上是一个超参数，代表在我们模型正则化下新的损失函数中，我们要让每一个θ尽可能的小，小的程度占我们整个损失函数的多少，如果α等于0，相当于没有正则化；如果α是正无穷的话，那么我们主要的优化任务就是让每一个θ尽可能的小。

岭回归 Ridge Regression

编程实现岭回归

岭回归 Ridge Regression

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)

from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict)

167.94010867293571

X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)

plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()

将绘制封装成函数

def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(poly_reg)

使用岭回归

from sklearn.linear_model import Ridge

def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])

# 注意alpha后面的参数是所有theta的平方和，而对于多项式回归来说，岭回归之前得到的θ都非常大
# 我们前面系数alpha可以先取的小一些（正则化程度轻一些）
# 第一个参数是degree20, 0.0001是第二个参数alpha
ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)

y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)

1.3233492754051845

# 通过使用岭回归，使得我们的均方误差小了非常多,曲线也缓和了非常多
plot_model(ridge1_reg)

ridge2_reg = RidgeRegression(20, 1)
ridge2_reg.fit(X_train, y_train)

y2_predict = ridge2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)

1.1888759304218448

# 让ridge2_reg 的alpha值等于1，均差误差更加的缩小，并且曲线越来越趋近于一根倾斜的直线
plot_model(ridge2_reg)

ridge3_reg = RidgeRegression(20, 100)
ridge3_reg.fit(X_train, y_train)

y3_predict = ridge3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)

1.3196456113086197

# 得到的误差依然是比较小，但是比之前的1.18大了些，说明正则化做的有些过头了
plot_model(ridge3_reg)

ridge4_reg = RidgeRegression(20, 10000000)
ridge4_reg.fit(X_train, y_train)

y4_predict = ridge4_reg.predict(X_test)
mean_squared_error(y_test, y4_predict)

1.8408455590998372

# 当alpha非常大，我们的模型实际上相当于就是在优化θ的平方和这一项，使得其最小（因为MSE的部分相对非常小）
# 而使得θ的平方和最小，就是使得每一个θ都趋近于0，这个时候曲线就趋近于一根直线了
plot_model(ridge4_reg)

LASSO回归

使用|θ|代替θ2来标示θ的大小

Selection Operator – 选择运算符

LASSO回归有一些选择的功能

实际编程（准备代码参考上一节岭回归）

LASSO

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_predict)

167.94010867293571

def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(poly_reg)

from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])

lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)

y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)

1.1496080843259966

plot_model(lasso1_reg)

lasso2_reg = LassoRegression(20, 0.1)
lasso2_reg.fit(X_train, y_train)

y2_predict = lasso2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)

1.1213911351818648

plot_model(lasso2_reg)

lasso3_reg = LassoRegression(20, 1)
lasso3_reg.fit(X_train, y_train)

y3_predict = lasso3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)

1.8408939659515595

plot_model(lasso3_reg)

总结Ridge和Lasso

α=100的时候，使用Ridge的得到的模型曲线依旧是一根曲线，事实上，使用Ridge很难得到一根倾斜的直线，他一直是弯曲的形状。

但是使用LASSO的时候，当α=0.1，虽然得到的依然是一根曲线，但是他显然比Radge的程度更低，更像一根直线。

这是因为LASSO趋向于使得一部分theta值为0（而不是很小的值），所以可以作为特征选择用，LASSO的最后两个字母SO就是Selection Operator的首字母缩写 使用LASSO的过程如果某一项θ等于0了，就说明LASSO Regression认为这个θ对应的特征是没有用的，剩下的那些不等于0的θ就说明LASSO Regression认为对应的这些特征有用，所以他可以当做特征选择用。

L1 范数常常用于特征选择

L2 范数常常用于防止模型过拟合

http://t.hengwei.me/post/%E6%B5%85%E8%B0%88l0l1l2%E8%8C%83%E6%95%B0%E5%8F%8A%E5%85%B6%E5%BA%94%E7%94%A8.html#1-l0-%E8%8C%83%E6%95%B0

https://zhuanlan.zhihu.com/p/29360425